2019-07-10프로그래밍 / 오디오

컴퓨터는 어떻게 소리를 들을까?

이번 포스팅에서는 필자의 예전 직업이었던 사운드 엔지니어의 추억을 살려서 한번 오디오에 대한 이론을 설명해볼까 한다. 하지만 이론 설명만 하면 노잼이니까 오디오 이론을 기초로 자바스크립트의 Web Audio API를 사용하여 간단한 오디오 파형까지 그려보려고 한다.

바로 코딩에 들어가고 싶지만 오디오에 관한 기본적인 지식이 있어야 오디오 파형을 그릴 때의 과정을 이해할 수 있으므로 이론을 최대한 지루하지 않게 설명하려고 한다. 이론이 코딩보다 재미없는 건 맞지만 오디오 파형을 그리려면 최소한 기본적으로 알고 있어야 하는 것들이니까 한번 쓱 흝어보자.

소리란 무엇일까?

제일 먼저 소리가 무엇인지부터 알아보자! 소리를 딱 한마디로 표현하자면 바로 진동이다. 기본적으로 우리가 소리를 듣는다는 것은 이런 순서로 일어난다.

어떤 물체가 부르르 진동을 한다. 이때 진동 주파수는 뭐 대충 440hz라고 치자.
그 물체 주변에 있는 매질이 440hz의 진동을 전달한다.(일반적인 상황에서는 주로 공기)
매질이 진동을 전달하면 우리의 고막도 440hz로 진동한다.
그 진동 신호를 달팽이관이 전기 신호로 바꿔서 청신경에 전달한다.
뇌가 신호를 받아서 해석한다. 440hz 접수완료!

이때 1번 순서에서 물체가 1초에 몇 번이나 떨렸는지 표현하기 위해 우리는 헤르츠(herz, hz) 단위를 사용한다. 10hz는 1초에 10번 진동을 했다는 의미이고 1khz는 1초에 1000번 진동을 했다는 것이다. 참고로 예시의 440hz는 도레미파솔라시도할 때 라음이다. 우리가 음악을 들을 때는 현악기면 현의 진동, 관악기면 입술이나 리드의 진동이 증폭된 것, 노래라면 성대의 진동을 듣게 되는 것이다. 아무리 감성터지는 음악도 공돌이 손에 걸리면 이렇게 분해될 수 있다.

우리가 듣는 아름다운 선율의 음악도 뜯어보면 그냥 진동 주파수 덩어리다.

이때 이 진동은 자연계에서 발생한 것이기 때문에 아날로그(Analog)의 형태로 나타난다. 사실 자연계에서 발생하는 대부분의 거시적인 신호는 아날로그 형태를 가지는데, 예를 들면 빛의 밝기가 변한다거나 바람의 세기가 변한다거나 소리의 크기가 변하는 등의 신호를 말한다.

소리는 아날로그 신호다

아날로그는 신호나 자료를 연속적인 물리량으로 나타낸 것이다. 이게 연속적인 물리량이라고 하면 뭔가 전문적이고 어려워보이는데 풀어보면 사실 별 거 없다. 여기서 우리가 집중해야할 단어는 물리량이 아닌 연속적이다.

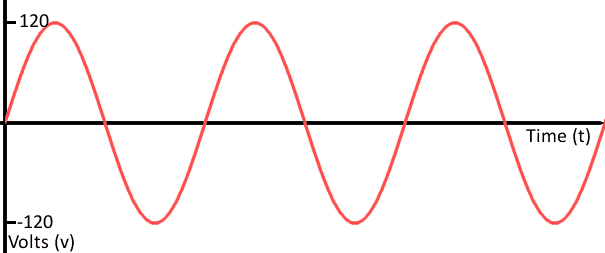가로 축은 시간, 세로 축은 전압이다. 아날로그 신호는 아무리 쪼개도 끝이 없는 연속성을 가진다

그렇다면 연속적이라는 건 무슨 말일까?

연속성의 대표적인 예는 바로 수이다. 자 우리가 이제 1부터 2까지 걸어간다고 생각해보자. 우리는 1에서 2까지 걸어가는 동안 몇개의 수를 만날 수 있을까?

우선 절반이 되는 위치에 있는 1.5가 있을 것이다. 그 절반인 1.25도 있을 것이며 또 그것의 절반인 1.125도 있을 것이다. 이런 식으로 계속 수를 쪼개다 보면 우리는 결국 이게 의미없는 삽질이라는 것을 깨닫게 된다. n/2를 계속 한들 끝이 있을리가 없기 때문이다. 만약 $10^{-10000}$ 단위까지 쪼갠다 해도 우리는 그 수를 계속 해서 무한히 쪼갤 수 있다. 우리는 이런 성질을 연속이라고 부른다.

이제 연속적이라는 말이 조금 이해가 되었길 바란다.

컴퓨터가 소리를 듣는 방법

근데 여러분도 알다시피 컴퓨터는 0과 1밖에 이해하지 못하는 바보다. 이 방식을 우리는 디지털(Digital)이라고 부른다. 그래서 0과 1밖에 모르는 컴퓨터는 연속성을 가진 아날로그 신호를 이해할 수가 없다.

그렇다면 우리가 자연에서 발생한 아날로그 형태인 소리를 컴퓨터가 듣게 해주려면 어떻게 해야할까?

간단하다. 아날로그를 디지털로 바꿔주면 된다. 아날로그 신호인 소리를 컴퓨터가 알아 들을 수 있게 변경하는 과정을 알고나면 Web Audio API가 우리에게 주는 정보들이 뭘 의미하는 지 알 수 있다. 그럼 지금부터 아날로그를 디지털로 변경하는 과정을 알아보자.

아날로그를 디지털로 변경하기 위해서는 몇가지 순서를 거쳐야 한다. 이 순서에서 어떤 값들을 사용하냐에 따라서 디지털로 변경된 소리의 해상도, 즉 음질이 결정된다. 이때 나오는 단어가 바로 샘플 레이트(Sample Rate)와 비트 레이트(Bit Rate)이다.

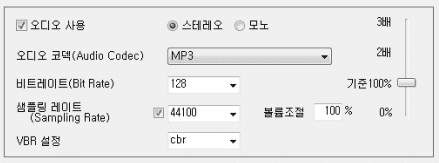인코더 프로그램 쓸 때 뭘 만져야 할지 모르게 만드는 어려운 단어들

단어는 어려워 보이지만 사실 간단하다. 결국 소리는 가로 축은 시간(Time), 세로 축은 진폭(Amplitude)으로 정의된 공간에 그려진 2차원의 진동 주파수 데이터이다. 이때 샘플 레이트는 가로 축의 해상도, 비트 레이트는 세로 축의 해상도를 의미하는 것이다. 이 값들은 아날로그를 디지털로 변경하는 첫번째 단계인 샘플링(Sampling)에서 활용된다.

샘플링(Sampling)

샘플링은 아날로그 신호를 디지털 신호로 바꾸기 위한 첫번째 단계이다. 위에서 설명한 것처럼 아날로그 신호인 소리는 연속적인 신호이기 때문에 컴퓨터가 이 신호를 그대로 이해할 수가 없다. 우리가 마이크를 사용하여 소리를 녹음할 때, 이 아날로그 신호는 결국 전기 신호로 변환되어 컴퓨터에게 주어진다. 소리의 진동이 마이크 안에 있는 장치에 전달되면 이 장치가 전압을 올렸다 내렸다 하면서 변환하는 원리이다.

하지만 우리의 바보 컴퓨터는 이렇게 까지 해줘도 이 전기 신호를 이해할 수 없다.

그래서 컴퓨터는 연속적인 전기 신호를 측정하기 위해 특정 타이밍을 정해서 이 타이밍마다 내가 전압을 측정할게!라는 꼼수를 사용한다. 컴퓨터가 꼼수를 쓰는 이 과정을 그림으로 나타내보면 이런 느낌이다.

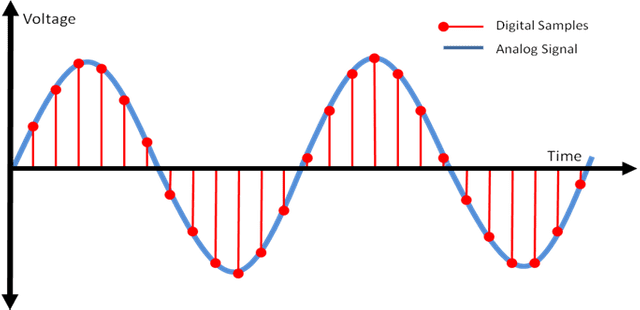
위 그림에 나타난 빨간 점이 컴퓨터가 전압을 측정한 타이밍이다. 컴퓨터는 특정 타이밍에 전기 신호를 측정하고 그 값을 저장한다. 빨간 점의 위치를 보면 저 신호는 [10, 20, 30, 27, 19, 8...] 뭐 이런 식으로 측정이 되었을 것이다. 이때 저 빨간 점을 더 세밀하게, 즉 컴퓨터가 샘플 측정을 하는 간격이 짧을 수록 우리는 원래 신호에 가까운 값을 측정할 수 있다.

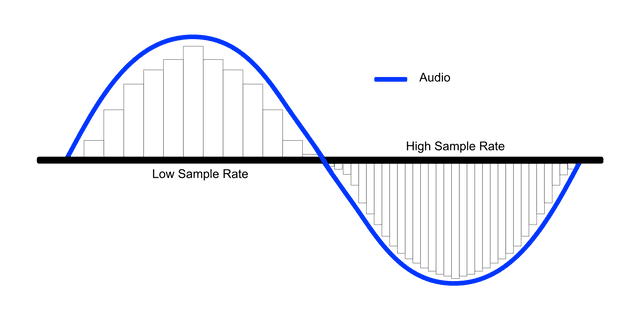신호 내부의 사각형이 컴퓨터가 이해한 신호의 모양이다.

이때 이 신호를 측정하는 간격을 샘플 레이트(Sample Rate)라고 하고 신호를 측정하는 과정 자체를 샘플링(Sampling)이라고 한다. 당연히 샘플 레이트가 높을 수록 소리의 해상도, 즉 음질이 더 좋을 수 밖에 없다. 특히 높은 주파수를 가진 소리, 즉 고음의 해상도가 확연하게 좋아진다.

보통 CD의 음질이 44.1kHz, TV나 라디오 방송이 48kHz의 샘플 레이트를 가지는데, 이는 약 1초에 44,100번, 48,000번 샘플을 측정한다는 것이다. 저 샘플 레이트는 어떤 기준으로 정하는 걸까?

샘플 레이트(Sample Rate)를 좀 더 자세히 알아보자

방금 설명했듯이 CD의 경우 샘플 레이트가 44.1kHz이다. 그 말인 즉슨 CD에 들어가는 오디오는 컴퓨터가 아날로그 신호를 1초에 44,100번 측정한 결과물인 것이라는 것이다.

하지만 인간이 들을 수 있는 영역인 가청주파수는 20hz ~ 20kHz 밖에 되지 않는다. 근데 왜 샘플 레이트는 44.1kHz, 48kHz처럼 훨씬 크게 잡는 것일까?

어차피 인간은 1초에 20,000번 진동하는 소리까지밖에 들을 수 없어서 44,100번 진동하는 소리를 녹음해도 어차피 들을 수 없는데?

이 질문에 대한 답은 소리의 진동 사이클이 어떻게 생겼는지를 보면 이해가 된다.

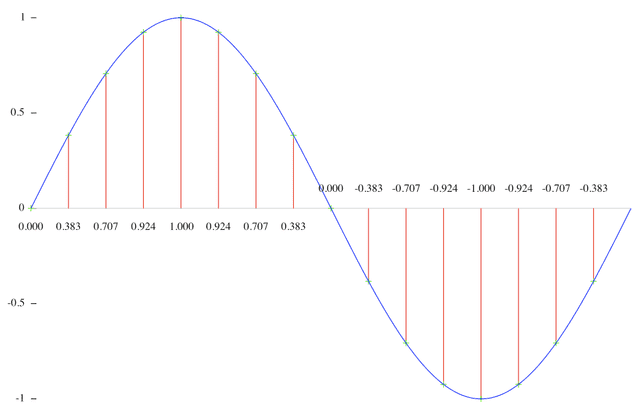
기본적으로 오디오 주파수는 이렇게 하나의 사이클 단위로 나누어 지는데, 이때 위로 올라가는 + 부분이 공기가 압축되는 부분이고 아래로 내려가는 - 부분이 다시 공기가 팽창하는 부분이다.

위에서 계속 설명했던 대로 소리란 곧 진동이고, 우리가 느끼는 것은 그 진동으로 인한 공기의 떨림이므로 압축 -> 팽창 -> 압축까지 모두 들어야 떨렸다!라고 느낄 수 있다는 것이다. 즉, 우리가 들을 수 있는 20,000번의 진동은 이 사이클이 1초에 20,000번 반복되는 소리라는 것이다.

압축이나 팽창 중에 하나만 주구장창 느낀다고 해서 이게 진동이구나라고 느낄 수는 없을 것이다.

그래서 오디오 신호의 한 사이클을 제대로 측정하려면 + 방향의 맨 위의 꼭지점 하나와 - 방향의 맨 밑의 꼭지점 하나를 모두 측정해야하기 때문에 최소 2번은 측정을 해야한다. 그래서 인간이 들을 수 있는 가장 높은 소리인 초당 20,000번의 떨림인 20kHz을 제대로 측정하려면 컴퓨터는 최소한 1초에 20,000 * 2 = 40,000번 측정을 해야 하는 것이다.

이게 바로 CD가 왜 44.1kHz의 샘플 레이트를 가지고 있는지에 대한 이유다. 이걸 나이퀴스트 이론(Nyquist Theorem)이라고 한다. 즉, 나이퀴스트 이론을 한마디로 정리하자면

측정하고 싶은 오디오 주파수있지? 오디오 신호 제대로 다 살리고 싶으면 최소한 그 주파수보다 두배는 더 빠르게 측정해야된다.
그러니까 최소한 측정하고 싶은 오디오 주파수의 두배 사이즈의 샘플 레이트를 준비하렴.

인 것이다. 근데 여기서 또 의문이 생긴다. 저 이론에 따르면 인간의 가청주파수는 20,000hz니까 딱 40,000번만 측정하면 인간이 들을 수 있는 소리는 다 녹음할 수 있는데 왜 44,100번이나 48,000번까지 측정하는 걸까?

자연에는 인간만 있는 것이 아니라 이런 친구들도 있기 때문이다.

안녕하세요 자연계 고음의 절대강자입니다. 쉬즈곤 정도는 밥먹으면서도 부를 수 있슴다.

사실 자연에는 우리가 듣지 못하는 훨씬 높은 소리들도 존재한다. 단지 우리가 20kHz까지밖에 못 들을 뿐이다. 뭐 박쥐나 돌고래 같은 친구들은 훨씬 고음역대의 소리를 내지 않는가?

근데 이 소리가 40kHz의 샘플 레이트를 준비한 그릇에 들어오면 어떻게 될까? 컴퓨터는 1초에 20,000번의 사이클을 도는 소리를 제대로 측정하려고 1초에 40,000번 전압을 측정하려고 했는데 만약 1초에 30,000번의 사이클을 도는 훨씬 더 높은 주파수의 소리가 들어와버린다면?

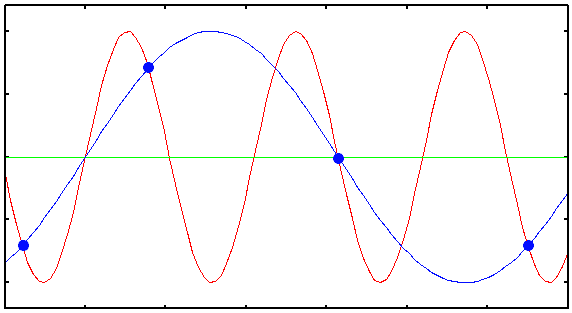
정답. 점을 이상한데다가 찍는다.

그림을 보면 컴퓨터가 점을 찍는 간격, 즉 전압을 측정하는 간격보다 들어온 신호의 사이클이 더 짧다. 그래서 컴퓨터가 찍은 점을 보면 신호의 꼭지점이 아닌 어중간한 어딘가에 찍힌 것을 볼 수 있다. 이것이 바로 나이퀴스트 이론의 가지고 있는 함정이다. 그리고 저 어중간한데 찍힌 점들을 이어본 파란색 선을 보면 결국 낮은 주파수가 된 것을 알 수 있다. 그러면 어떻게 될까?

우리 귀에 아주 잘 들린다. 참 소름돋는 순간이다! 녹음할 때는 분명히 아무것도 안들렸는데 녹음한 걸 들어보니 이상한 소리가 녹음되어있으니 말이다. 그래서 이 현상을 고스트 주파수(Ghost Frequency)라고 부른다.

아니 그러면 샘플 레이트를 팍팍 올리면 되잖아! 높은 소리도 제대로 녹음되면 문제 해결 아닌가?

하지만 이 디지털 오디오 기술이 처음 사용되기 시작한게 1970년대이기 때문에 무작정 샘플 레이트를 올리기에는 하드웨어 용량이 못 따라갔었다.

그래서 이 문제를 해결하기 위해 사용한 방법이 바로 LPF(Low Pass Filter)이다. 이 필터는 전기 쪽 공부하신 분들은 매우 익숙할텐데, 말 그대로 낮은(Low) 주파수만 통과(Pass)시키는 필터이다. 오디오 녹음을 할때 LPF를 사용해서 인간의 가청주파수보다 높은 소리는 다 잘라버리고 인간의 가청주파수 영역의 소리만 통과시키면 방금 얘기한 고스트 주파수가 생길 일도 없기 때문이다.

근데 또 아날로그 신호라는 게 그렇게 무 자르듯이 싹뚝! 잘리는 게 아니다.

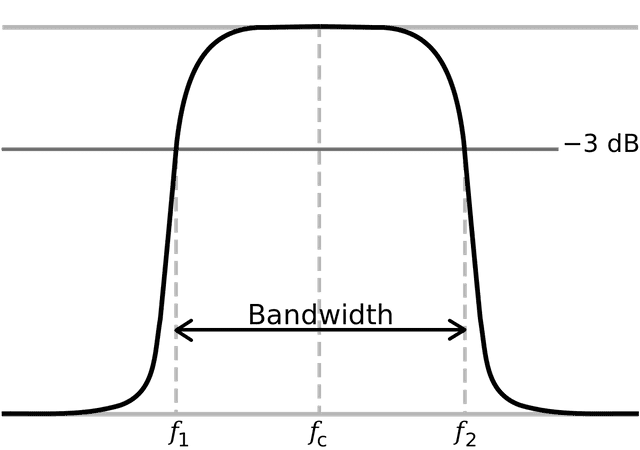
LPF를 써도 결국 잘린 부분이 저렇게 비스듬하게 꺾이면서 약간 아쉬운 부분이 남게된다. 이때 그림에 표시된 허용 범위인 -3db 밑으로 떨어지기 시작하는 곳을 Cut Off라고 부른다. 저기에서부터 신호가 잘렸다고 치겠다는 것이다. 그럼 Cut Off되는 부분을 20kHz보다 조금 더 밑으로 내리면 20kHz 언저리에서 신호가 사라지게 만들 수 있지 않을까? 라는 생각도 들지만 그 문제 때문에 20kHz의 주파수 영역을 전부 활용하지 못하는 건 너무 아깝다고 판단이 들었나보다.

그래서 Cut Off를 딱 20kHz에 맞추고 남는 부분은 그냥 감수하자고 합의가 된 것이다. 당시 기술로 저 남는 부분을 줄이고 줄여서 맞춘게 딱 2,050hz였다.

그럼 이제 남는 부분과 가청주파수를 합쳐보면 22,050hz가 된다. 나이퀴스트 이론에 따르면 우리는 최소한 2배의 샘플 레이트를 준비해야 이 신호를 제대로 측정할 수 있으므로 결국 CD의 표준 샘플 레이트가 44,100hz = 44.1kHz가 된 것이다. 뭐 그 외에도 당시 기술의 한계 외에도 기업들끼리 싸우기도 하고 어른의 사정도 있는 등 국제 표준을 정할 때 늘 발생하는 여러가지 이슈가 있었지만 대표적인 기술적인 이슈는 이 이유였다.

그 후 48kHz, 96kHz, 192kHz 등의 높은 샘플 레이트는 그냥 디바이스가 발전하면서 기술적인 제한이 없어졌으니까 “샘플 레이트는 클수록 좋지! 뿜뿜”하면서 늘린 것이다.

비트 레이트(Bit Rate)

비트 레이트는 샘플링에 비하면 초 간단하다. 특히 우리 같은 개발랭이들에게 익숙한 이름인 Bit가 붙어있지 않은가? 샘플 레이트가 소리의 가로 해상도 역할을 한다면 비트 레이트는 세로 해상도 역할을 한다.

샘플 레이트와 마찬가지로 비트 레이트도 CD를 기준으로 설명하는 게 보편적이기 때문에 다시 CD를 기준으로 설명하겠다.

CD의 비트 레이트는 16bit인데 이건 말 그대로 세로로 16bit 만큼의 해당하는 값을 표현할 수 있다는 얘기이다. 아까 위에서 설명한 샘플링을 진행할 때 전압을 측정했었다. 이때 컴퓨터가 측정한 이 전압의 값을 얼마나 섬세하게 표현할 수 있느냐를 비트 레이트가 결정하는 것이다. 16bit면 16자리의 이진법을 사용할 수 있다는 것이고 $2^{16} = 65536$ 이니까 0~65536까지 총 65537개의 값을 사용할 수 있는 것이다.

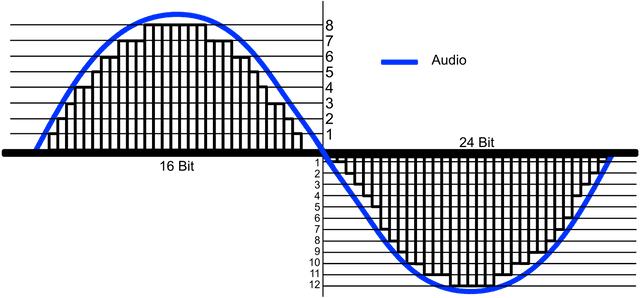비트 레이트가 높을 수록 아날로그 신호 내부의 막대가 더 꼼꼼하게 채워지는 것을 볼 수 있다.
+와 -를 합쳐서 비트를 세는 `signed`이기 때문에 그림에는 50% 씩만 표현되어있는 것이다.

물론 아날로그인 소리 신호가 변환된 전압 값이 123 같이 딱 떨어지는 정수일리가 없으므로 우리가 사용할 수 있는 0~65536 중 근사치를 찾아서 바꿔주는데 이 과정을 양자화(Quantizing)이라고 부른다. (양자역학에서 나오는 그 양자랑 같은 의미 맞다.)

이후 0~65536의 값으로 변경된 전압을 컴퓨터가 이해할 수 있는 이진수(Binary)로 변경하는 과정을 부호화(Coding)라고 한다.

이런 것들은 우리같은 개발랭이들은 워낙 익숙한 문제이기 때문에 이 정도만 설명하고 넘어가겠다.

Web Audio API로 파형 그려보기

자, 드디어 길고 길었던 소리 이론이 끝났다. 필자는 디지털로 변환된 오디오를 가지고 파형을 그려보는 것이 목적이기 때문에 Analog to Digital만 다뤘고 Digital to Analog는 이 포스팅에서 다루지 않겠다. 근데 이것도 나름 재밌으므로 따로 찾아보길 강추한다. 필자는 오디오 파일을 업로드해서 해당 오디오 파일을 Web Audio API로 분석하여 필요한 데이터를 뽑아내고 svg를 사용하여 파형을 그릴 것이다.

참고로 프로젝트는 webpack4와 babel7을 사용하여 초간단하게 구성했다. 자세한 코드는 깃허브 레파지토리에서 확인 해볼 수 있다.

기본 틀 잡기

그럼 먼저 HTML을 간단하게 작성하자.

<body>
  <input id="audio-uploader" type="file">
  <svg id="waveform" preserveAspectRatio="none">
    <g id="waveform-path-group"></g>
  </svg>
</body>

HTML은 이게 끝이다. 오디오 파일을 업로드할 input 엘리먼트 하나와 파형을 그릴 svg 엘리먼트 하나만 있으면 된다. 어차피 테스트 용도라서 UI가 중요한게 아니기 때문에 기능 구현에 충실했다.(라고 포장을 해봅니다)

이제 파일이 업로드되면 실행될 이벤트 핸들러를 작성하자.

// index.js
(function () {
  const inputDOM = document.getElementById('audio-uploader');
  inputDOM.onchange = e => {
    const file = e.currentTarget.files[0];
    if (file) {
      const reader = new FileReader();
      reader.onload = e => console.log(e.target.result);
      reader.readAsArrayBuffer(file);
    }
  }
})();

FileReader.prototype.readAsArrayBuffer 메소드는 바이너리 형태인 파일을 한번에 반환하는 것이 아니라 일정 단위의 청크(Chunk)로 반환하는 메소드이다. 보통 뭐 서버로 파일 업로드 한다거나 할 때 많이 사용한다. 원래는 이 ArrayBuffer를 처리해주기 위한 별도의 로직을 작성해야하지만 이번에 사용할 Web Audio API가 내부적으로 ArrayBuffer를 알아서 처리해주기 때문에 걱정하지 않아도 된다.

AudioAnalyzer 클래스 작성

이제 본격적인 Web Audio API를 사용해볼 차례이다. 필자는 별도로 AudioAnalyzer라는 싱글톤 클래스를 만들었다.

// lib/AudioAnalyzer.js
class AudioAnalyzer {
  constructor () {
    if (!window.AudioContext) {
      const errorMsg = 'Web Audio API 지원 안돼유 ㅜㅜ';
      alert(errorMsg);
      throw new Error(errorMsg);
    }

    this.audioContext = new (AudioContext || webkitAudioContext)();
    this.audioBuffer = null;
    this.sampleRate = 0;
    this.peaks = [];

    this.waveFormBox = document.getElementById('waveform');
    this.waveFormPathGroup = document.getElementById('waveform-path-group');
  }

  reset () {
    this.audioContext = new (AudioContext || webkitAudioContext)();
    this.audioBuffer = null;
    this.sampleRate = 0;
    this.peaks = [];
  }
}

export default new AudioAnalyzer();

SVG 뷰박스를 설정하자

이렇게 대충 기본 틀을 잡아주고 나서 오디오 파형을 그릴 svg 엘리먼트의 뷰박스를 설정할 수 있는 메소드를 하나 선언할 것이다. 소리 신호는 샘플 레이트에 따라서 들어온 데이터의 길이가 천차만별이기 때문에 뷰박스의 width를 오디오 데이터의 크기에 맞게 동적으로 변경해줘야지 모든 신호를 뷰박스에 딱 맞게 그릴 수 있다.

updateViewboxSize () {
  this.waveFormBox.setAttribute('viewBox', `0 -1 ${this.sampleRate} 2`);
}

svg 엘리먼트의 viewBox 속성은 앞에서부터 min-x, min-y, width, height를 의미한다. 비트 레이트를 설명할 때 얘기 했듯이 오디오 신호는 부호를 가지는 signed이기 때문에 0, 0이 아닌 0, -1에서 뷰박스를 설정해야한다. 그리고 width는 오디오의 샘플 레이트로 잡아줘서 오디오 신호가 뷰박스의 처음부터 끝까지 꽉 차도록 설정하고 height는 -1 ~ 1까지 잡아줘야하니까 2로 설정했다.

이렇게 선언한 updateViewboxSize메소드는 어플리케이션이 초기화될때 뷰박스 사이즈도 함께 초기화되도록 constructor와 reset 메소드에 적당히 추가해주었다.

업로드된 AudioBuffer 확인하기

이제 input 엘리먼트를 통해 업로드된 오디오 파일을 디코딩하는 귀여운 setter를 하나 선언하면 된다.

setAudio (audioFile) {
  this.audioContext.decodeAudioData(audioFile).then(buffer => {
    console.log(buffer);
  });
}

AudioContext.prototype.decodeAudioData 메소드는 ArrayBuffer를 받아서 AudioBuffer로 변환하는 메소드이다. 아까 위에서 설명했던 대로 readAsArrayBuffer 메소드가 반환한 ArrayBuffer는 한번에 모든 바이너리 데이터를 불러오는 것이 아니라 청크 단위로 불러오기 때문에 decodeAudioData도 변환을 동기적으로 해주지는 않는다. 그래서 이 메소드를 사용할 때는 콜백함수를 사용하거나 Promise를 사용해야 한다.

이제 실제로 오디오 파일이 어떻게 변환되는지 보기 위해 파일을 업로드하면 AudioAnalyzer에게 오디오 파일을 넘기도록 변경해주자.

// index.js
import AudioAnalyzer from './lib/AudioAnalyzer';

(function () {
  const inputDOM = document.getElementById('audio-uploader');
  inputDOM.onchange = e => {
    const file = e.currentTarget.files[0];
    if (file) {
      // AudioAnalyzer 초기화
      AudioAnalyzer.reset();
      const reader = new FileReader();
      // AudioAnalyzer에게 파일 토스
      reader.onload = e => AudioAnalyzer.setAudio(e.target.result);
      reader.readAsArrayBuffer(file);
    }
  }
})();

이 쯤 했으면 이제 메인 함수에는 더 이상 뭘 작성할 필요가 없을 것 같다. 이제 AudioAnalyzer만 가지고 놀면 된다. 데이터가 어떻게 나오는 지 확인하기 위해 필자가 좋아하는 가수인 거미의 그대 돌아오면.mp3 파일을 업로드 해보았다.

AudioBuffer {
  length: 12225071,
  duration: 277.2124943310658,
  sampleRate: 44100,
  numberOfChannels: 2
}

그러면 AudioAnalyzer의 setAudio 메소드 내부에서 실행된 decodeAudioData가 ArrayBuffer를 받아서 AudioBuffer로 변환한 뒤 반환해준다. 이걸 뜯어보면 유용한 정보들이 들어있다.

sampleRate: 당연히 샘플 레이트를 의미하고 이 곡의 샘플 레이트는 44,100hz이다.
numberOfChannels: 이 오디오가 몇개의 채널을 가지고 있는지를 나타내는데 이 파일은 두 개의 채널이 있는 스테레오 채널 오디오 파일이다.
length: 피크(Peak)들의 개수를 의미한다. 피크는 컴퓨터가 샘플링을 진행할 때 전압을 측정한 값을 의미한다.
duration: 이 오디오 파일의 재생 길이를 초단위로 표시해준다. 그대 돌아오면은 약 277초동안 재생되나보다.

음 여기서 한가지 결정해야할 것이 생겼다. 채널이 $n$ 개인 오디오 데이터가 들어왔을 때 그 $n$ 개의 채널의 오디오 파형을 모두 표현해주거나 채널을 하나로 합쳐서 파형을 표현해주어야한다. 필자는 $n$ 개의 채널을 가진 오디오 데이터가 들어오더라도 그 채널을 모두 한개의 채널로 머지해서 파형을 그릴 예정이다.

하지만 이 포스팅에서 채널을 머지하는 것까지 모두 이야기하면 너무 복잡해지기 때문에 그냥 하나의 채널만 사용하여 진행하도록 하겠다.

오디오 데이터 분석하고 정제하기

이제 필자는 기본적인 오디오 데이터인 AudioBuffer를 얻었다. 이제 이 데이터만 있어도 오디오 파형을 그릴 수 있다. 이제 AudioBuffer에서 필요한 데이터만 뽑아서 클래스의 멤버변수들에 할당해주자.

setAudio (audioFile) {
  this.audioContext.decodeAudioData(audioFile).then(buffer => {
    // AudioBuffer 객체를 멤버변수에 할당
    this.audioBuffer = buffer;
    // 업로드된 오디오의 샘플 레이트를 멤버변수에 할당
    this.sampleRate = buffer.sampleRate;
    // 샘플 레이트에 맞춰서 svg 엘리먼트 크기 조정
    this.updateViewboxSize();
  });
}

후, 여기까지 왔으면 파형을 그릴 준비가 모두 끝났다. 우선 AudioBuffer에서 오디오 신호를 하나하나 뽑아보자.

먼저 오디오 신호가 들어있는 배열부터 한번 살펴보자. 아까 필자가 AudioBuffer의 데이터를 간략하게 봤을 때 numberOfChannels라는 프로퍼티가 있었고 이 값이 2인 스테레오 채널이었다. 이 채널 데이터는 AudioBuffer.getChannelData 메소드를 통해서 가져올 수 있다.

for (let i = 0; i < this.audioBuffer.numberOfChannels; i++) {
  console.log(this.audioBuffer.getChannelData(i));
}

// Float32Array(12225071) [0, 0, 0, …]
// Float32Array(12225071) [0, 0, 0, …]

아닛 어마무시한 길이의 Float32Array가 나왔다. 지금 필자에게 보이는 값은 전부 0이지만 보통 음악이 시작하자마자 쿠과과광! 하진 않기 때문에 그런거지 뒤쪽 인덱스의 엘리먼트에는 값이 제대로 들어가 있다. 그렇다고 이 값들을 그대로 사용하긴 조금 힘들고 조금 손질을 해줘야 한다.

우선 저 배열에 들어있는 원소의 정체가 뭔지부터 생각해보자. 배열의 길이인 12225071를 사용하면 이 친구의 정체를 파악할 수 있다. 아까 우리가 AudioBuffer를 통해 이 곡의 재생길이(Duration)를 봤을 때 약 277초 였다. 이 곡의 샘플 레이트와 재생길이를 곱해보면 12225071이 나온다. 즉, 저 원소들은 컴퓨터가 샘플 레이트에 따라 측정한 전압인 피크이다.

저 하나하나의 피크들이 전부 Float32Array의 원소로 들어가있다.

일단 저 원소의 정체가 피크라는 것을 알았으니 이 친구들을 조금 정제해보자. 왜 이걸 정제하느냐?

12,225,071개의 피크를 전부 렌더한다는 게 과연 효율적인 시각화인가…?

라는 합리적 의심 때문이다. 솔직히 피크가 천만개가 찍히던 오백만개가 찍히던 어차피 우리는 조그만 모니터로 볼 것이기 때문에 굳이 이걸 하나하나 다 표현해준다는 것 자체가 큰 의미는 없다.

그래서 필자는 피크들을 적당히 압축할 것이다. 모든 피크를 수집하는 것이 아니라 적당한 길이의 샘플을 만들고 해당 샘플 안의 최대값과 최소값만 수집할 것이다.

위에서 설명했듯이 나이퀴스트 이론에 따르면 어차피 하나의 사이클을 표현할때 최대값 한개와 최소값 한개만 알면 아무 문제가 없다. 파형의 해상도는 조금 떨어지겠지만 이건 뭐 상용 툴도 아니기 때문에 큰 의미는 없다.

const sampleSize = peaks.length / this.sampleRate;
const sampleStep = Math.floor(sampleSize / 10);

// 예시로 0번 채널만 가져옴
const peaks = this.audioBuffer.getChannelData(0);
const resultsPeaks = [];

// 딱 샘플 레이트 길이인 44100개의 피크만 수집할 것이다.
Array(this.sampleRate).fill().forEach((v, newPeakIndex) => {
  const start = Math.floor(newPeakIndex * sampleSize);
  const end = Math.floor(newPeakIndex + sampleSize);

  let min = peaks[0];
  let max = peaks[0];

  for (let sampleIndex = start; sampleIndex < end; sampleIndex += sampleStep) {
    const v = peaks[sampleIndex];
    if (v > max) {
      max = v;
    }
    else if (v < min) {
      min = v;
    }
  }

  resultPeaks[2 * newPeakIndex] = max;
  resultPeaks[2 * newPeakIndex + 1] = min;
});

좀 복잡해보이지만 이 코드를 한마디로 표현하면 다음과 같다.

샘플레이트 만큼 이터레이션을 돈다.

특정 길이의 2차 샘플 구간을 정하고 그 구간 내에서 최대값과 최소값을 찾는다.

resultPeaks 배열의 짝수 인덱스에 최대값을, 홀수 인덱스에는 최소값을 삽입한다.

resultsPeaks배열에 값을 저장할 때 2 * newPeakIndex와 같이 배열의 크기를 2배로 해주는 이유는 피크를 한번 이터레이션 돌 때 max와 min 최대 2개의 값을 저장해야하기 때문이다.

이렇게 해서 필자는 적당히 압축된 88200 길이의 피크 배열 하나를 얻게 되었다.

이제 진짜 그려보자!

그리는 방법은 생각보다 단순하다. 위에서 뽑아온 피크 배열을 순회돌면서 그려주기만 하면 된다.

SVG의 path 엘리먼트는 d 속성에 담긴 문자열을 분석하여 선을 그려준다. 이때 M은 Move, 그림을 그릴 포인터를 옮기는 명령어이고 L은 Line, 지정한 곳까지 선을 긋는 명령어이다.

즉, 우리는 포인터를 옮기고 선을 긋고를 반복하면 되는 것이다. 아까 필자가 짝수 인덱스에는 최대 값을 담고 홀수 인덱스에는 최소값을 담아준 이유가 바로 여기에 있다. 이터레이션을 돌면서 짝수 인덱스 일때는 M 명령어를 사용하여 포인터를 옮기고 홀수 인덱스 일때는 L 명령어를 사용하여 선을 그리려고 한 것이다.

draw () {
  if (this.audioBuffer) {
    const peaks = this.peaks;
    const totalPeaks = peaks.length;

    let d = '';
    for(let peakIndex = 0; peakIndex < totalPeaks; peakIndex++) {
      if (peakNumber % 2 === 0) {
        d += ` M${Math.floor(peakNumber / 2)}, ${peaks.shift()}`;
      }
      else {
        d += ` L${Math.floor(peakNumber / 2)}, ${peaks.shift()}`;
      }
    }

    const path = document.createElementNS('http://www.w3.org/2000/svg', 'path');
    path.setAttributeNS(null, 'd', d);

    this.waveFormPathGroup.appendChild(path);
  }
}

Math.floor(peakNumber / 2)는 $x$ 축, peaks.shift()는 $y$ 축을 의미한다. 이 코드는 대략 이런 식으로 작동할 것이다. 앞에 붙은 숫자는 피크의 인덱스라고 생각하자.

(0, 100)으로 포인터 이동

(0, -25)으로 선을 긋는다.

(1, 300)으로 포인터 이동

(1, -450)으로 선을 긋는다.

쭉쭉 반복

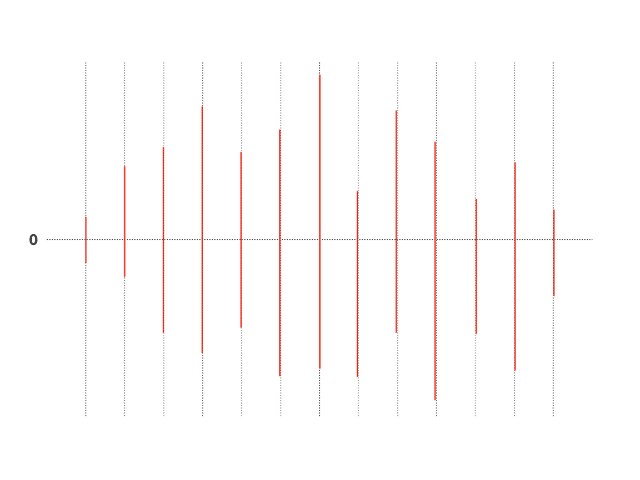저 과정을 반복하면 대략 이런 모양의 작대기들이 그려진다

우리가 그리려는 오디오 파형은 디지털 신호를 표현한 것이기 때문에 위에서 우리가 봤던 오디오 신호의 예시처럼 연속적인 아날로그로는 표현이 불가능 하다. 그래서 이렇게 작대기를 쭉쭉 그어가면서 표현해야하는 것이다. 이렇게 보면 상당히 허접한 그림이 나올 것 같지만, 저 선이 88,200개가 겹쳐있으면 꽤 그럴싸해보인다.

작대기도 잘 그으면 예술이 된다

자, 이렇게 오디오 파형을 심플하게 그려보았다. 여기까지 해놓고 하는 말인데… 사실 WaveSurfer라고 이거 해주는 라이브러리가 있다. 기능도 더 많다.

그냥 내 손으로 한번 직접 그려보고 싶었다.

음악 주세요 DJ

파형만 그리기는 좀 아쉬우니 막간을 이용해서 메소드 하나만 더 만들어보자. 바로 이 음악을 재생하는 기능이다. 원래 이 메소드를 만들 때 필자의 의도는 음악이라도 좀 들으면서 만들자였는데 이거 만들면서 그대 돌아오면을 너무 많이 들어서 조금 질려버렸다.(거미 누나 미안…)

play (buffer) {
  const sourceBuffer = this.audioContext.createBufferSource();
  sourceBuffer.buffer = buffer;
  sourceBuffer.connect(this.audioContext.destination);
  sourceBuffer.start();
}

AudioContext.prototype.createBufferSource 메소드는 AudioNode 중 하나인 AudioBufferSourceNode라는 친구를 생성하는 메소드인데, 이 AudioNode에게 우리가 지금까지 가지고 놀았던 AudioBuffer를 넘겨주면 진짜 오디오적인 컨트롤을 할 수가 있게 도와주는 음…껍데기 같은 느낌이다.

Web Audio API는 이런 AudioNode들을 서로 연결해서 소리를 변조할 수 있는 기능을 제공하기 때문에 이걸 사용해서 컴프레서나 리버브 같은 오디오 이펙터도 만들 수 있다. 다음에는 한번 오디오 이펙터를 만들어보는 것을 목표로 해야겠다.

완성된 샘플의 소스는 필자의 깃허브 레파지토리에서, 라이브 데모는 여기서 확인할 수 있다.

이상으로 컴퓨터는 어떻게 소리를 들을까? 포스팅을 마친다.