2019-10-12프로그래밍 / 알고리즘

최소 값과 최대 값을 빠르게 찾을 수 있게 도와주는 힙(Heap)

이번 포스팅에서는 대표적인 자료 구조 중 하나인 힙(Heap)에 대한 설명과 구현을 한번 해보려고 한다.

이전의 포스팅에서 몇 번 언급한 적이 있지만 필자는 지금 백수다. 이제 프라하에서 한 달간의 힐링도 끝났으니 슬슬 면접을 보러 다녀야 하는데, 모두들 알다시피 면접에서는 기초 알고리즘이나 자료 구조에 대한 질문이 들어올 확률이 굉장히 높다. 하지만 필자는 최근 1년 정도 기초 공부를 게을리 했기 때문에 다시 공부를 해야하는 상황이다.

그래서 일단은 자료 구조부터 다시 살펴볼 생각인데, 그 중 제일 기억이 잘 나지 않는 힙(Heap)부터 한번 부셔볼까 한다.

힙(Heap)이란?

힙은 기본적으로 완전 이진 트리(Complete Binary Tree)를 기본으로 한 자료 구조이며, 부모 노드와 자식 노드 간의 대소관계가 성립하는 자료 구조이다. 그렇기 때문에 힙의 루트 노드는 힙 내의 데이터들 중 가장 큰 값이거나 가장 작은 값이라고 할 수 있다.

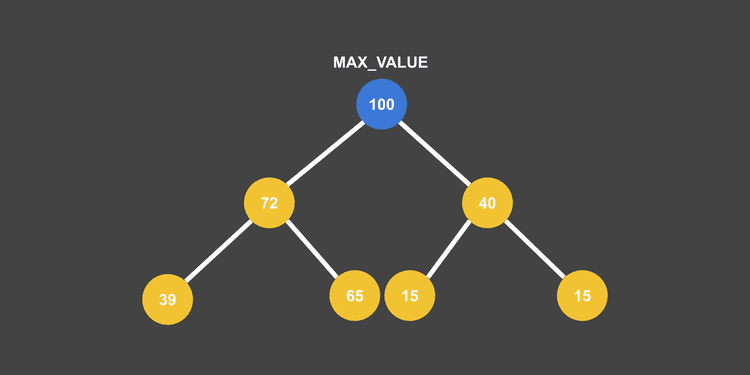
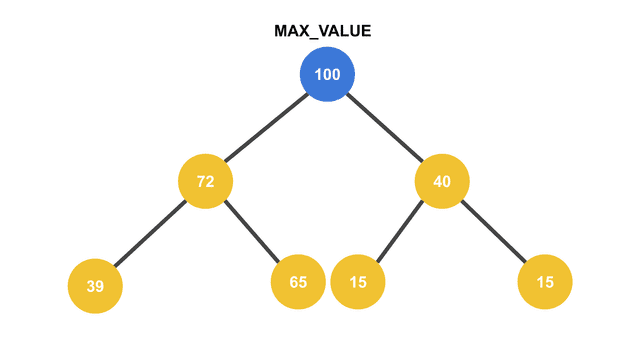루트에 최대 값이 오게 되는 Max Heap의 모습
생긴 건 완전 이진 트리랑 똑같이 생겼다

즉, 힙 내의 가장 큰 값이나 가장 작은 값에 접근하고 싶을 때 비교 연산없이 한번에 접근할 수 있다는 의미이며, 이 접근 연산의 시간 복잡도는 당연히 $O(1)$ 이다. 이런 힙의 성격 때문에 힙은 여러 개의 데이터 중에서 가장 크거나 작은 값을 빠르게 찾아야 하는 영역에서 유용하게 사용된다.

사실 단순히 어떤 데이터 뭉치 안에서 최대 값이나 최소 값에 $O(1)$ 의 시간 복잡도로 접근하고 싶다면 그냥 링크드 리스트(Linked List)나 배열(Array)을 정렬해서 사용해도 무방하긴 하다. 한번 정렬만 해놓으면 그 다음부터는 그냥 헤드에서 값을 쏙쏙 뽑아다 쓰면 되기 때문이다.

그러나 이렇게 정렬되어 있는 데이터 뭉치에 새로운 데이터를 추가할 때는 전체 데이터 뭉치를 싹 다 뒤져서 다시 최대, 최소 값이 무엇인지 찾아내고 재정렬하는 과정을 거쳐야한다.

배열과 링크드 리스트과 같은 선형 자료 구조는 이 과정에 $O(n)$ 의 시간 복잡도가 소요되는 반면, 부모가 자식보다 크거나 작게 정렬된 이진 트리의 경우는 새로운 추가된 노드의 부모 노드들과만 비교해도 정렬 상태를 유지할 수 있기 때문에 $O(\log n)$ 의 시간 복잡도만 소요된다.

즉, 정렬하고 싶은 데이터가 많을 수록 더 유리하다는 소리다.

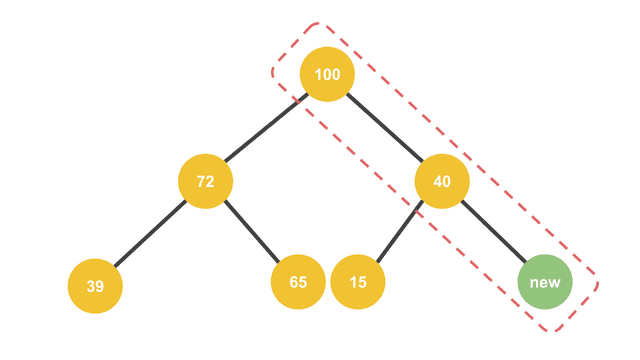전체 데이터를 비교할 필요없이 이 부분만 비교하면 다시 재정렬할 수 있다

힙은 완전 이진 트리를 기초로 하기 때문에 구현하는 방법 또한 완전 이진 트리와 흡사하다. 그렇기 때문에 힙을 구현해보기에 앞서 완전 이진 트리의 특징을 먼저 이야기 해보려고 한다.

완전 이진 트리(Complete Binary Tree)

먼저, 힙의 기본이 되는 완전 이진 트리의 특징을 한번 살펴보자. 이진 트리(Binary Tree)란 어떤 하나의 노드가 자식 노드를 최대 2개까지만 가질 수 있는 트리를 말한다.

그 말인 즉슨, 한 레벨에 최대로 들어설 수 있는 노드의 개수가 정해져있다는 뜻이고, 노드들에게 고유한 인덱스를 부여할 수 있다는 것을 의미한다.

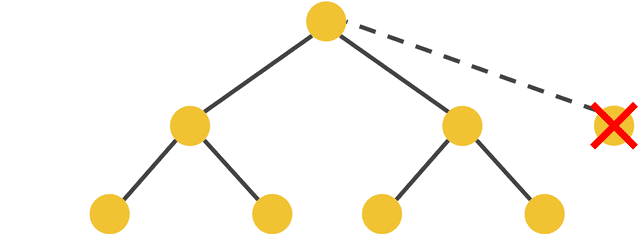부모 노드는 반드시 2개 이하의 자식 노드를 가져야 한다.

완전 이진 트리(Complete Binary Tree)는 이진 트리의 노드를 생성할 때 트리의 왼쪽부터 차곡차곡 채워 나가는 트리를 의미한다. 이때 완전 이진 트리의 한 레벨이 꽉 차기 전에는 다음 레벨에 노드를 생성할 수 없다. 즉, 마지막 레벨을 제외한 모든 레벨에는 노드가 꽉 차 있어야 한다는 뜻이다.

트리는 보통 링크드 리스트(Linked List)나 배열(Array)과 같은 선형 자료 구조를 사용하여 구현하는데, 이때 링크드 리스트와 배열의 특징에 따라 장단점이 갈리기 때문에 선택이 필요하다.(링크드 리스트와 배열의 차이에 대한 내용은 이 포스팅의 주제가 아니므로 따로 설명하지는 않겠다.)

일반적으로 트리는 링크드 리스트를 사용하여 구현하지만 완전 이진 트리의 경우에는 배열로 구현하는 것이 더 효율적이다.

배열이 더 효율적인 이유

사실 트리를 구현할 때 원소에 한방에 접근이 가능하다는 배열의 최대 장점을 뒤로 미뤄두고서라도 링크드 리스트를 사용하는 이유는, 배열을 사용하여 트리를 구현하면 메모리 고정 할당 방식이라는 배열의 특성 상 불편한 점이 너무 많기 때문이다.

그러나 완전 이진 트리에서는 이 불편한 점들이 사라지기 때문에 배열의 장점을 오롯이 가져갈 수 있다.

원하는 노드로의 접근이 쉽다

이건 배열의 최대 장점인 인덱스만 알면 해당 원소에 바로 접근이 가능하다는 장점을 그대로 살린 것이다. 이진 트리는 각 레벨에 들어설 수 있는 노드의 최대 개수가 정해져 있기 때문에 간단한 수식만으로 특정 노드의 인덱스를 알아내어 $O(1)$ 의 시간 복잡도로 노드에 접근할 수 있다.

먼저, 특정 노드를 기반으로 부모나 자식 노드에 접근하고 싶다면 다음과 같이 인덱스를 계산해볼 수 있다.

루트 노드가 0번 인덱스를 가지고, 현재 노드가 $i$ 번 인덱스를 가지고 있을 때

[부모 노드] $(i-1) / 2$ [왼쪽 자식 노드] $2i+1$ [오른쪽 자식 노드] $2i+2$

위와 같이 특정 노드의 인덱스를 기반으로 부모와 자식들의 인덱스를 알아내는 방법도 있지만, 배열로 만든 완전 이진 트리의 진짜 장점은 간단한 수식을 통해서 원하는 레벨, 원하는 순번의 노드로 바로 접근할 수도 있다는 것이다.

완전 이진 트리의 성질을 이용하면 특정 레벨까지의 최대 노드 개수인 $c$ 를 간단히 계산할 수 있기 때문에 가능한 일이다.

c = 2^{level} - 1

function getAllNodeCountByLevel (level = 1) {
  return 2**level - 1;
}

console.log(getAllNodeCountByLevel(3));

7 // 3 레벨로 구성된 완전 이진 트리 내 노드의 최대 개수

이 식을 사용하면 $n$ 번째 레벨의 $m$ 번째 노드의 인덱스도 간단하게 알아낼 수 있다.

예를 들어, 완전 이진 트리의 n 레벨에 있는 m번째 노드의 인덱스인 $i$ 를 구하고 싶다면, 내가 접근하고 싶은 레벨의 바로 위 레벨인 $n - 1$ 레벨까지의 모든 노드의 개수 $c$ 을 구하고, 거기에 해당 레벨 내에서 내가 $m$ 번째 노드에 접근하고 싶은지만 더해주면 된다.

i = c + m - 1

function getNodeIndex (level = 1, count = 1) {
  return getAllNodeCountByLevel(level - 1) + count - 1;
}

console.log(getNodeIndex(3, 3));

5 // 3 레벨의 3 번째로 위치한 노드의 인덱스

마지막에 1을 빼주는 이유는 우리가 구하고 싶은 것이 노드의 순번이 아닌 인덱스이기 때문이다. 배열의 인덱스는 0부터 시작한다는 사실을 잊지 말자.

이처럼 배열로 구현한 완전 이진 트리는 간단한 계산만으로 원하는 노드에 접근하기가 용이하지만, 링크드 리스트로 구현하게되면 원하는 노드에 바로 접근할 수 없고, 트리를 순회하여 접근해야한다.

배열의 원소를 뒤로 밀어줘야 할 일이 없다

배열은 메모리에 연속적인 공간을 할당하여 사용하기 때문에, 배열 중간에 원소를 끼워넣으려면 새로운 메모리 공간을 확보하기 위해 원소를 한 칸씩 뒤로 밀어줘야하는 슬픈 상황이 발생하지만, 링크드 리스트는 그냥 prev 값과 next 값만 변경함으로써 중간에 새로운 원소를 끼워넣기가 편하다.

그러나 이진 트리의 경우, 자식 노드를 최대 2개까지만 가질 수 있다는 제약이 있기 때문에 높이가 $h$ 인 트리는 최대 노드 개수가 $2^{h} -1$ 개로 정해져있다. 즉, 이 크기 만큼만 배열을 메모리에 할당하고 나면 중간에 노드를 새로 삽입하기 위해 배열의 원소를 뒤로 밀어야하는 경우가 발생하지 않는다는 것이다.

트리가 기울어지지 않는다

일반적으로 배열로 구현한 트리가 기울어지게 되면 메모리 공간에 심한 낭비가 생기게 되는데, 그 이유는 그림으로 보면 이해하기가 한결 편하다.

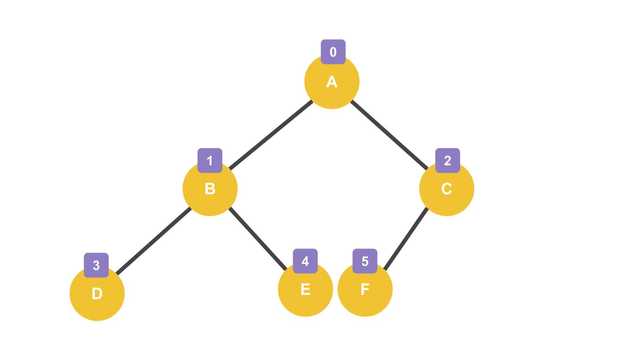
위 그림은 이상적으로 균형이 잡힌 밸런스드 이진 트리(Balanced Binary Tree)의 모습이다. 만약 이 트리를 배열로 구현한다면 메모리에는 이렇게 값들이 담길 것이다.

Location	0	1	2	3	4	5
Value	A	B	C	D	E	F

배열 중간에 빈 공간이 없이 차곡차곡 메모리에 담겼다. 노드의 인덱스는 트리의 왼쪽부터 순차적으로 부여되기 때문에 자식 노드를 왼쪽부터 생성한다면 메모리에 빈 공간을 만들지 않을 수 있다.

물론 자식 노드를 생성할 때 왼쪽을 건너 뛰고 오른쪽부터 생성하면 빈 공간이 생기긴 하지만, 더 큰 문제는 트리가 한 쪽으로 크게 기울어지게 되게 되는 편향 트리가 되는 경우이다.

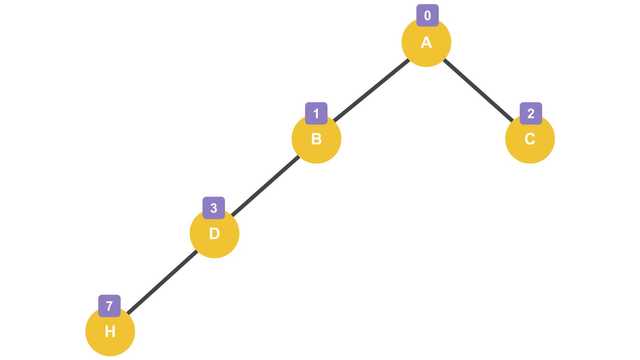
Location	0	1	2	3	4	5	6	7
Value	A	B	C	D	-	-	-	H

위 그림처럼 한 쪽으로 크게 기운 편향 트리는 중간 인덱스를 건너뛰고 다음 레벨에 노드를 생성한 경우이기 때문에 메모리에 빈 공간이 생길 수 밖에 없다. 그렇기 때문에 메모리 공간이 낭비된다고 하는 것이다. 물론 오른쪽으로 기울었다면 건너뛰어야 하는 인덱스도 더 크기 때문에 메모리 공간의 낭비가 더 심해진다.

그러나 완전 이진 트리는 노드를 왼쪽부터 차곡차곡 채워나가고, 한 레벨의 노드가 다 채워지기 전까지는 다음 레벨에 노드를 채울 수 없다는 제약들이 걸려있기 때문에 애초에 트리가 기울어질 일 자체가 없으니 메모리에 빈 공간이 생길 일도 없다.

이런 이유들로 인해 완전 이진 트리는 원소에 바로 접근이 가능한 배열의 장점을 살려서 구현하는 경우가 많고, 완전 이진 트리를 기반으로 하는 힙 또한 마찬가지 이유로 인해 주로 배열로 구현하게된다.

완전 이진 트리와 힙의 차이

힙(Heap)은 완전 이진 트리를 기초로 하기 때문에 기본적인 노드의 삽입 및 삭제 알고리즘은 일반적인 완전 이진 트리와 동일하다. 노드의 삽입은 반드시 배열의 끝에만 가능하며, 노드를 삭제하고 나면 빈 공간이 남지 않도록 남은 노드들을 다시 당겨서 빈 공간을 채워줘야한다.

다만 힙은 부모와 자식 노드 간의 대소관계가 성립되어야 한다는 조건이 있기 때문에, 삽입 및 삭제 후 노드를 다시 정렬해주는 기능이 추가로 필요하다.

또한 힙은 사실 트리 내의 최대 값이나 최소 값을 쉽게 찾고자 하는 자료 구조이기 때문에, 트리 중간에 위치한 노드에 바로 접근할 일도 거의 없다. 항상 Array[0]에 위치한 루트 노드를 뽑아다 쓰면 되기 때문이다. 루트 노드를 뽑아온다는 것은 곧 루트 노드의 삭제를 의미하기 때문에 마찬가지로 힙을 다시 정렬해줘야한다.

힙은 최대 힙(Max Heap)과 최소 힙(Min Heap)으로 나누어지는데, 최대 힙은 항상 부모의 값이 자식보다 커야하고, 최소 힙은 반대로 부모의 값이 자식보다 작아야 한다. 즉, 최대 힙의 루트는 힙 내에서 가장 큰 값, 최소 힙의 루트는 힙 내에서 가장 작은 값을 의미한다는 것이다.

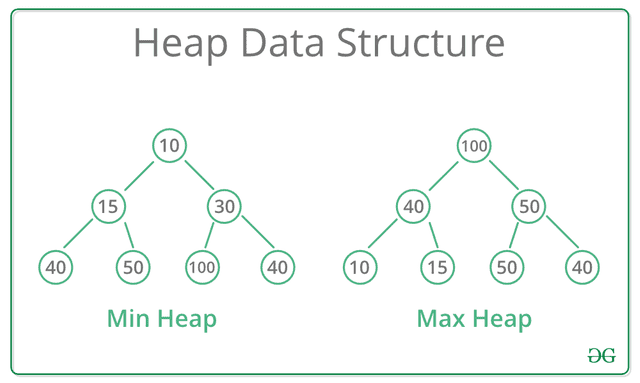
즉, 힙을 구현한다는 것은 완전 이진 트리를 구현하고, 최대 힙과 최소 힙에 맞는 정렬 기능을 추가하면 된다는 것이다.

힙을 구현해보자

일단 최대 힙과 최소 힙의 차이는 사실 정렬할 때 조건 밖에 없으니, 필자는 최대 힙만 구현해보려고 한다. 위에서 이야기 했듯이 완전 이진 트리의 경우는 링크드 리스트를 이용하는 것보다 배열을 이용하는 것이 더 효율적이기 때문에 배열을 이용하여 구현할 것이다.

일단 작고 귀여운 MaxHeap 클래스를 하나 만들어주자.

class MaxHeap {
  constructor () {
    this.nodes = [];
  }
}

만약 링크드 리스트로 구현하고자 한다면 Node 클래스를 별도로 선언해서 사용하겠지만 필자가 사용할 자료 구조는 배열이기 때문에 단촐하기 그지 없다. 그럼 이제 힙에 값을 삽입하는 메소드부터 한번 만들어보도록 하자.

새로운 값의 삽입. 버블 업!

힙에 새로운 값을 삽입할 때는 완전 이진 트리의 규칙대로 무조건 트리의 왼쪽부터 채워나간다. 그 말인 즉슨, 그냥 push 메소드를 사용하여 배열의 꼬리로 값을 하나씩 쑤셔넣어주면 된다는 것이다. 잘 이해가 되지 않는다면 위의 완전 이진 트리 설명 부분을 다시 읽어보도록 하자.

insert (value) {
  this.nodes.push(value);
}

최대 힙은 항상 부모가 자식보다 큰 값을 가져야한다는 제약이 있으므로, 만약 우리가 힙에 삽입한 노드가 부모 노드보다 큰 값을 가지고 있다면 두 노드의 위치를 바꿔줘야한다.

그리고 이 작업을 현재 삽입한 노드가 루트까지 올라가거나, 부모보다 작은 값을 가지게 되거나, 두 조건 중 하나를 만족할 때까지 반복한다.

이때 새로 추가한 값이 부모 노드와 스왑되면서 점점 트리의 위로 올라가는 모양새가 거품이 뽀글뽀글 올라오는 모양새랑 비슷하다고 해서 버블 업(Bubble Up)이라고 부른다.

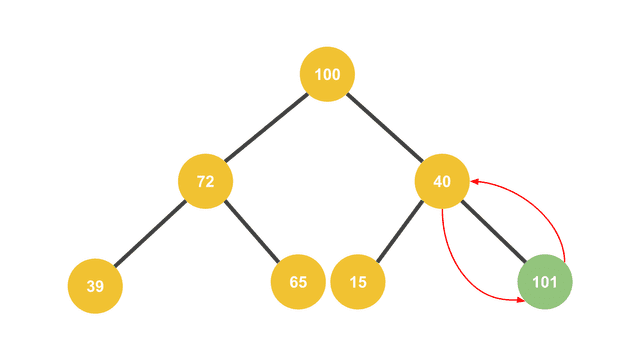부모와 자리를 바꾸면서 트리의 위쪽으로 점점 올라간다

insert (value) {
  this.nodes.push(value);
  this.bubbleUp();
}

bubbleUp (index = this.nodes.length - 1) {
  if (index < 1) {
    return;
  }

  const currentNode = this.nodes[index];
  const parentIndex = Math.floor((index - 1) / 2);
  const parentNode = this.nodes[parentIndex];

  if (parentNode >= currentNode) {
    return;
  }

  this.nodes[index] = parentNode;
  this.nodes[parentIndex] = currentNode;
  index = parentIndex;
  this.bubbleUp(index);
}

bubbleUp 메소드는 인자로 받은 인덱스의 노드의 값과 부모 노드의 값을 비교하여, 해당 노드가 부모 노드의 값보다 큰 값을 가지고 있다면 두 노드의 위치를 스왑하는 역할을 한다. 트리의 특성 상 이 작업은 분할 정복이 가능한 부분이므로 재귀 호출로 구현하였다.

여기까지 작성하고 간단히 테스트를 해보면 힙 내의 가장 큰 값이 배열의 헤드, 즉 트리의 루트에 위치하게 된다는 것을 알 수 있다.

const heap = new MaxHeap();
heap.insert(1);
heap.insert(3);
heap.insert(23);
heap.insert(2);
heap.insert(10);
heap.insert(32);
heap.insert(9);

console.log(heap.nodes);

[ 32, 10, 23, 1, 2, 3, 9 ]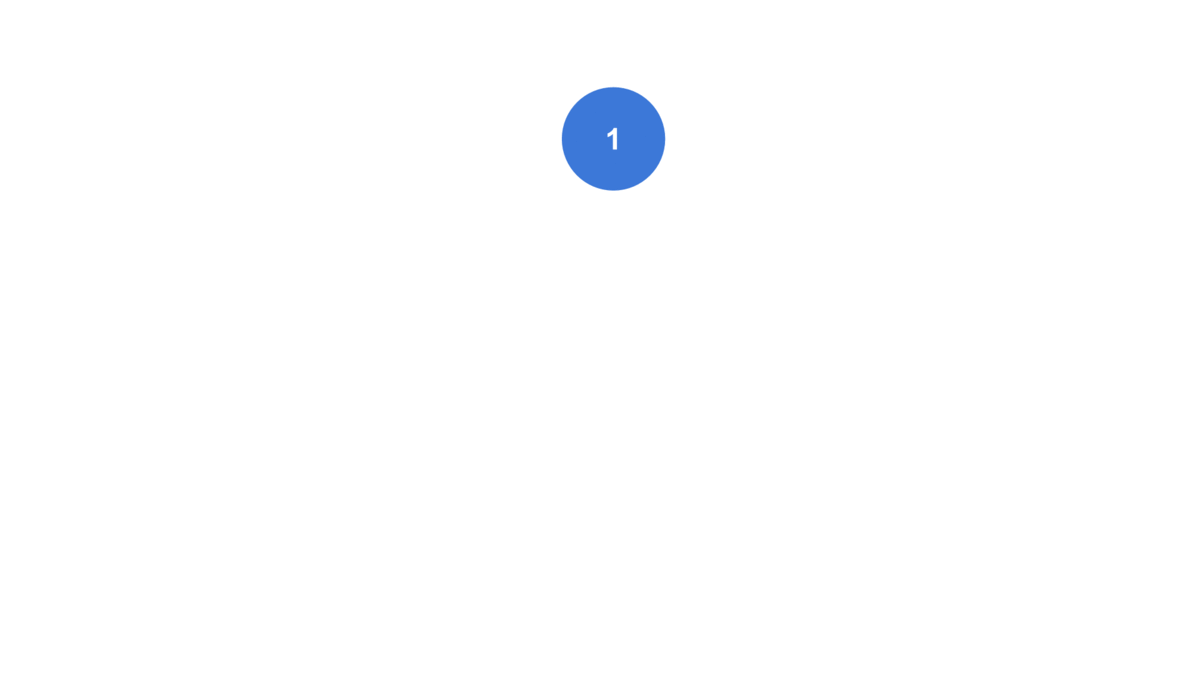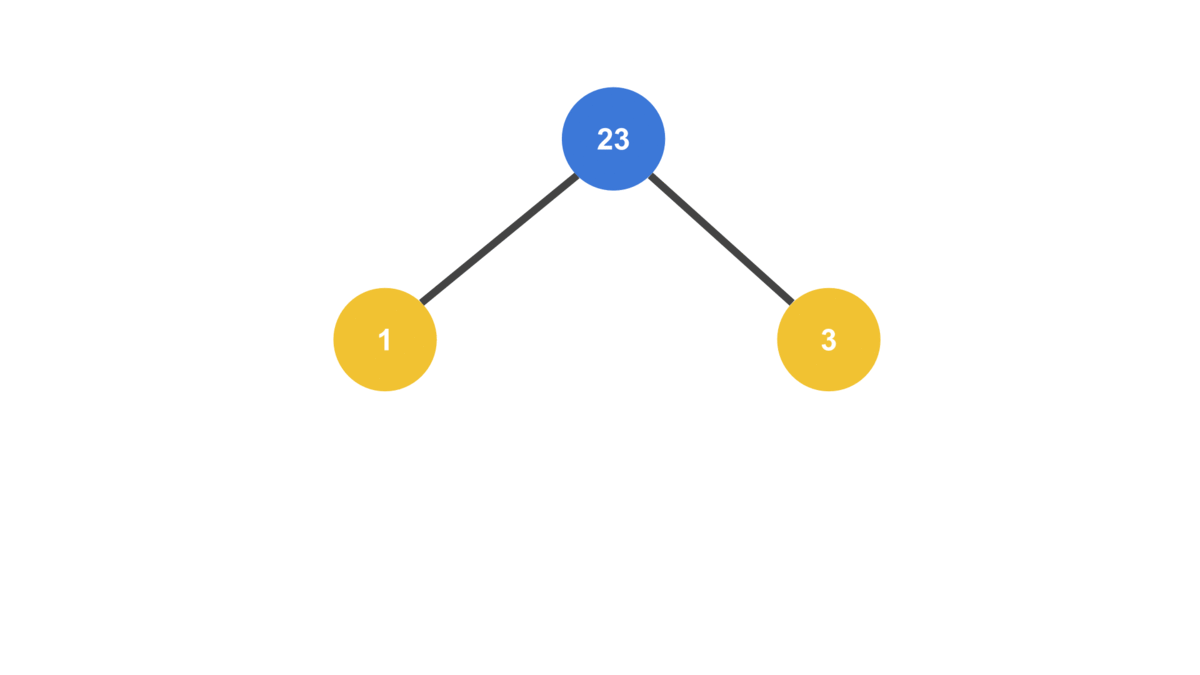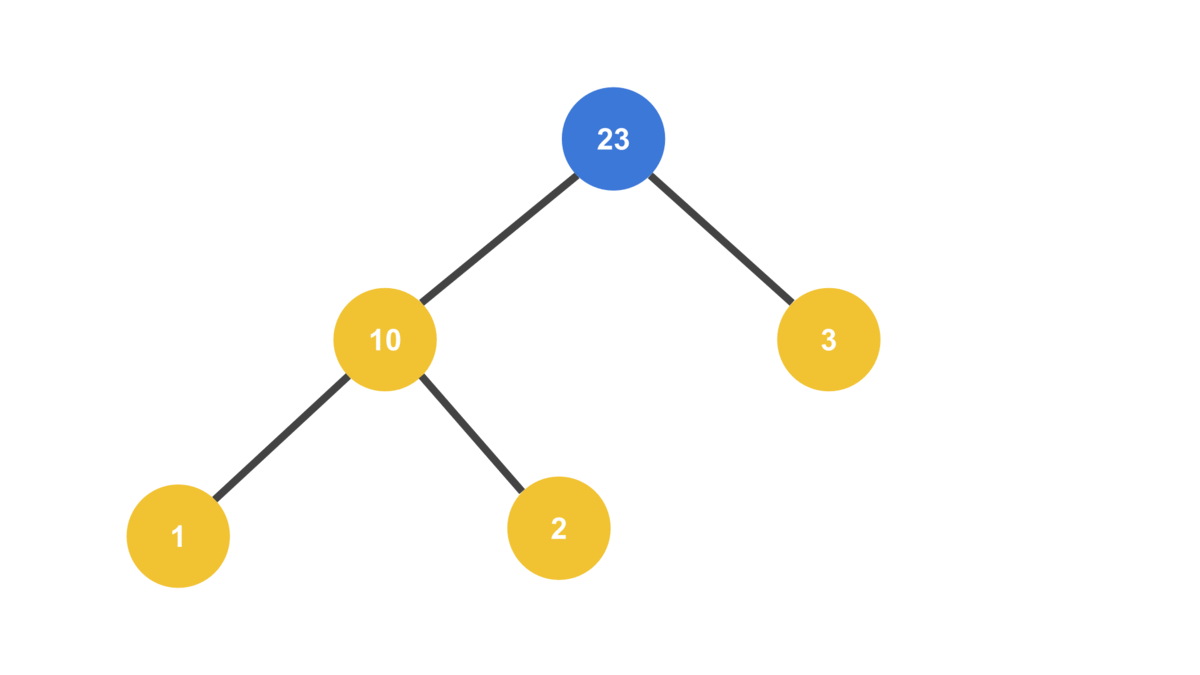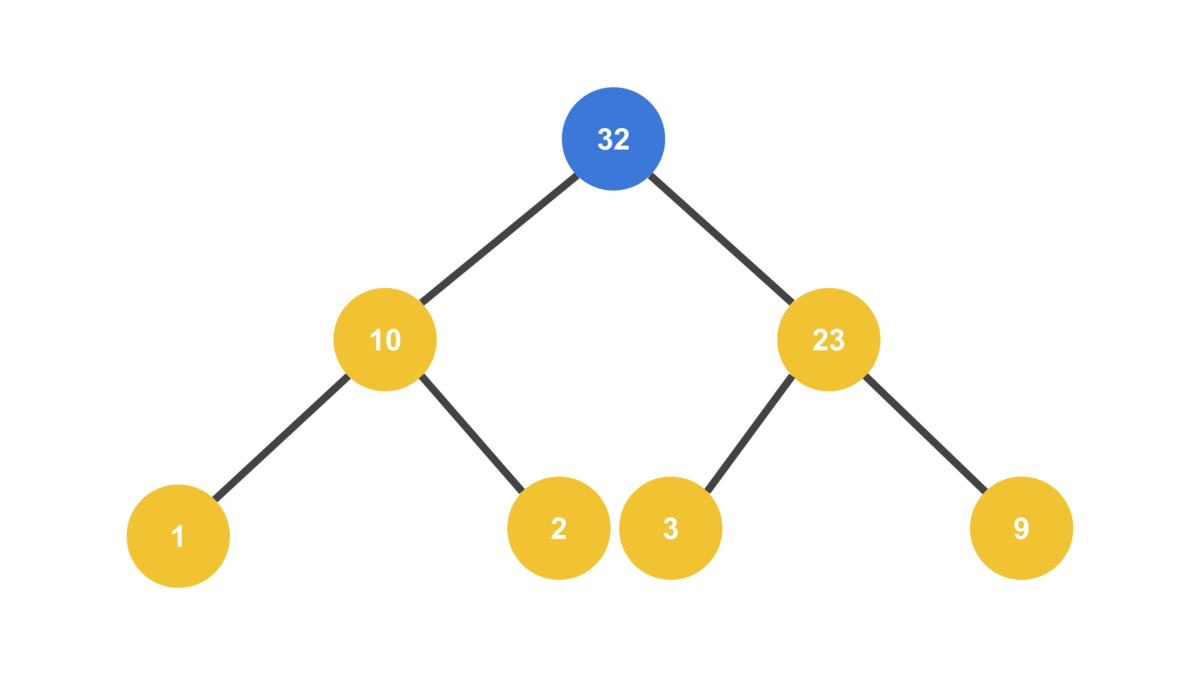

부모보다 큰 값이 추가되면 부모와 자리를 바꾼다

루트에서 값을 빼오자. 트릭클 다운!

값의 삽입과 버블 업을 구현해보았으면 이번에는 루트에서 값을 빼오는 메소드를 만들어보자. 즉, 삭제 연산이다. 이 경우 루트 노드를 뽑아버리면 루트 노드의 자리가 비게 되니 힙을 재정렬해서 다시 루트 노드를 채워줘야한다.

이때 기존 루트 노드의 자식 노드들을 루트 노드로 올리는 것이 아니라 트리의 가장 마지막에 위치한 노드를 가져와서 루트 노드로 삽입하게 되는데, 이는 수정될 힙에서 빈 공간이 생기지 않게 함으로써 연산량을 줄이기 위해서이다.

바로 루트의 바로 밑에 있는 자식들을 끌어올려서 루트로 사용해버리면 자연스럽게 그 노드가 있던 곳은 공백이 생기게 되고, 그럼 또 다음 레벨에서 어떤 노드를 끌여올려야 할지 비교 연산이 필요하게 되기 때문이다.

그리고 힙은 반드시 완전 이진 트리의 형태를 유지해야하기 때문에 이 과정에서 트리가 한 쪽으로 기울게 되버리면 또 트리의 균형을 맞춰줘야하는 번거로움도 생길 수 있다.

그래서 가장 마지막에 위치한 노드를 새로운 루트 노드로 사용하고 자식들과 값을 비교해나가면서 자리를 바꿔나가는데, 이때 새로운 루트 노드가 트리의 아래 쪽으로 점점 이동하는 모양새가 물방울이 떨어지는 모양새랑 비슷하다고 해서 트릭클 다운(Trickle Down)이라고 부른다.(컴퓨터 용어 주제에 왠지 갬성적이다…)

extract () {
  const max = this.nodes[0];
  this.nodes[0] = this.nodes.pop();
  this.trickleDown();

  return max;
}

trickleDown (index = 0) {
  const leftChildIndex = 2 * index + 1;
  const rightChildIndex = 2 * index + 2;
  const length = this.nodes.length;

  let largest = index;

  if (leftChildIndex <= length && this.nodes[leftChildIndex] > this.nodes[largest]) {
    largest = leftChildIndex;
  }
  if (rightChildIndex <= length && this.nodes[rightChildIndex] > this.nodes[largest]) {
    largest = rightChildIndex;
  }

  if (largest !== index) {
    [this.nodes[largest], this.nodes[index]] = [this.nodes[index], this.nodes[largest]];
    this.trickleDown(largest);
  }
}

트릭클 다운 또한 버블 업과 마찬가지로 재귀 호출을 통한 분할 정복으로 해결할 수 있다.

trickleDown 메소드는 부모 노드와 왼쪽 자식 노드, 오른쪽 자식 노드의 값을 비교한 후 자식 노드가 부모 노드보다 큰 값을 가지고 있다면 부모 노드와 해당 자식 노드의 위치를 변경한다.

쉽게 말하면 세 개의 노드 중 가장 큰 값을 가지고 있는 놈이 부모 자리를 먹는 것인데, 만약 이 힘싸움에서 밀린 것이 부모 노드라면 자신의 자식이 있던 곳으로 좌천되는 것이라고 보면 된다.

썩씌딩하는 꼬라지가 왠지 이 놈을 닮았다

만약 이 과정에서 부모 노드와 자식 노드의 위치가 변경되었다면 변경된 부모 노드의 인덱스를 다시 tickleDown 메소드의 인자로 넘겨서 이 과정을 계속 반복한다.

여기까지 작성했으면 버블 업과 마찬가지로 간단한 테스트를 한번 해보자. 힙에 들어가는 값은 이전에 버블 업에서 사용했던 값과 동일한 값들을 사용했다.

const heap = new MaxHeap();
heap.insert(1);
heap.insert(3);
heap.insert(23);
heap.insert(2);
heap.insert(10);
heap.insert(32);
heap.insert(9);

const length = heap.nodes.length;
for (let i = 0; i < length; i++) {
  console.log('MAX_VALUE = ', heap.extract());
  console.log('HEAP = ', heap.nodes);
}

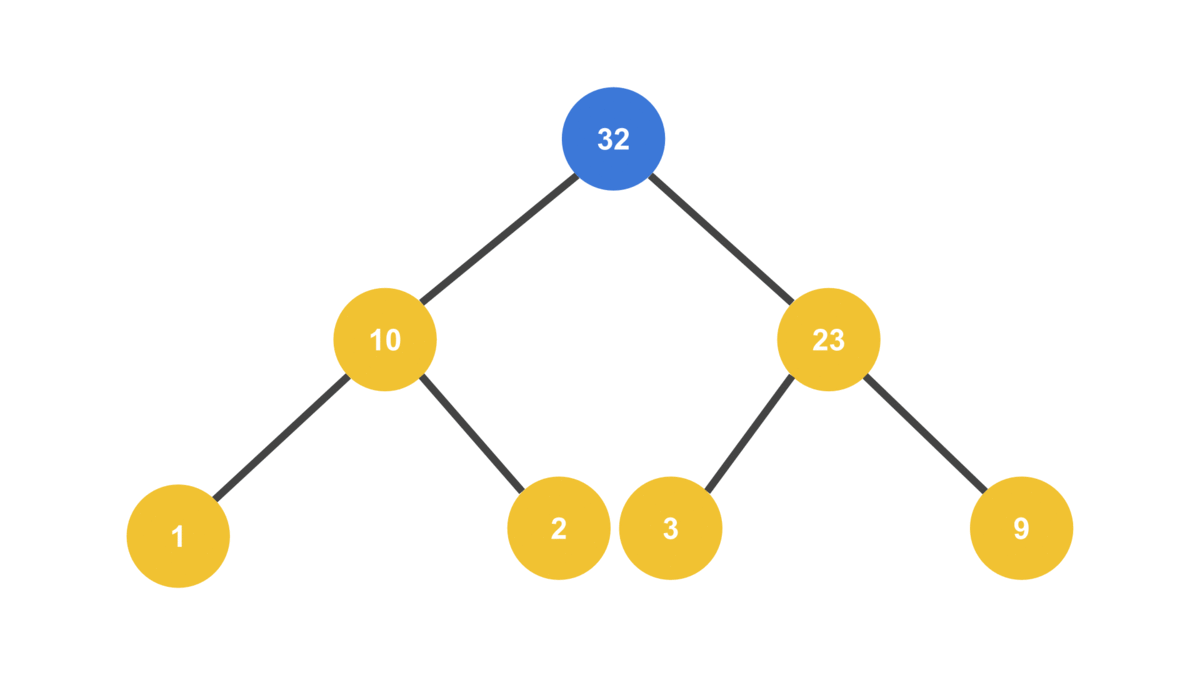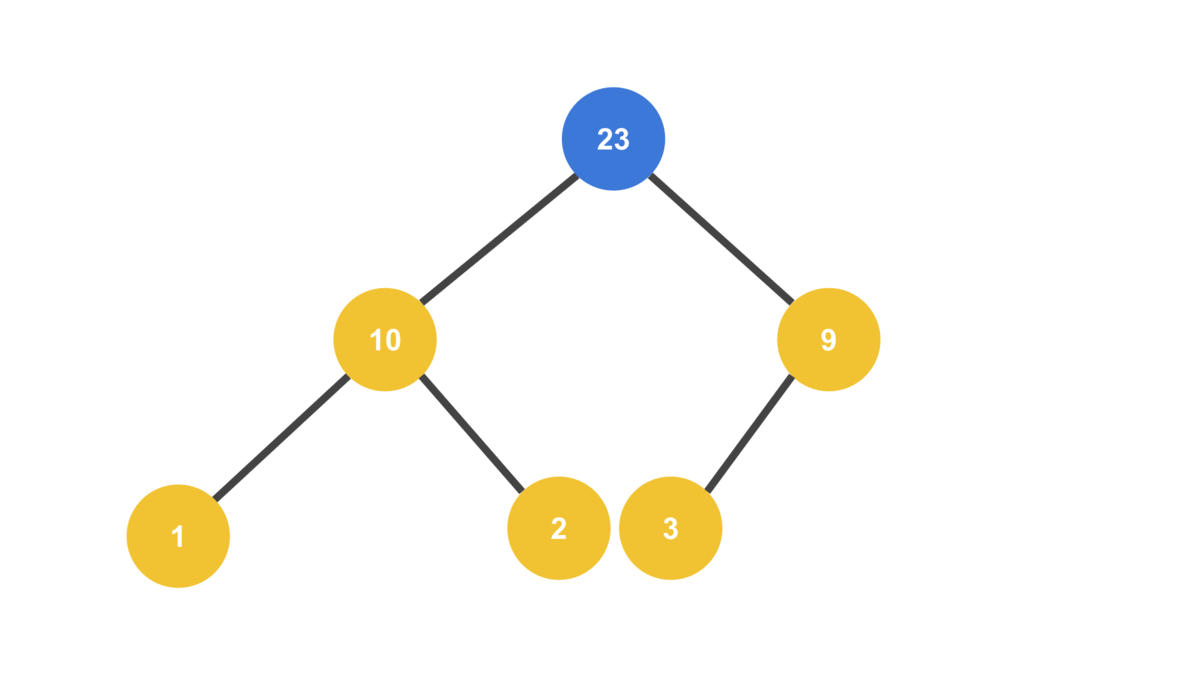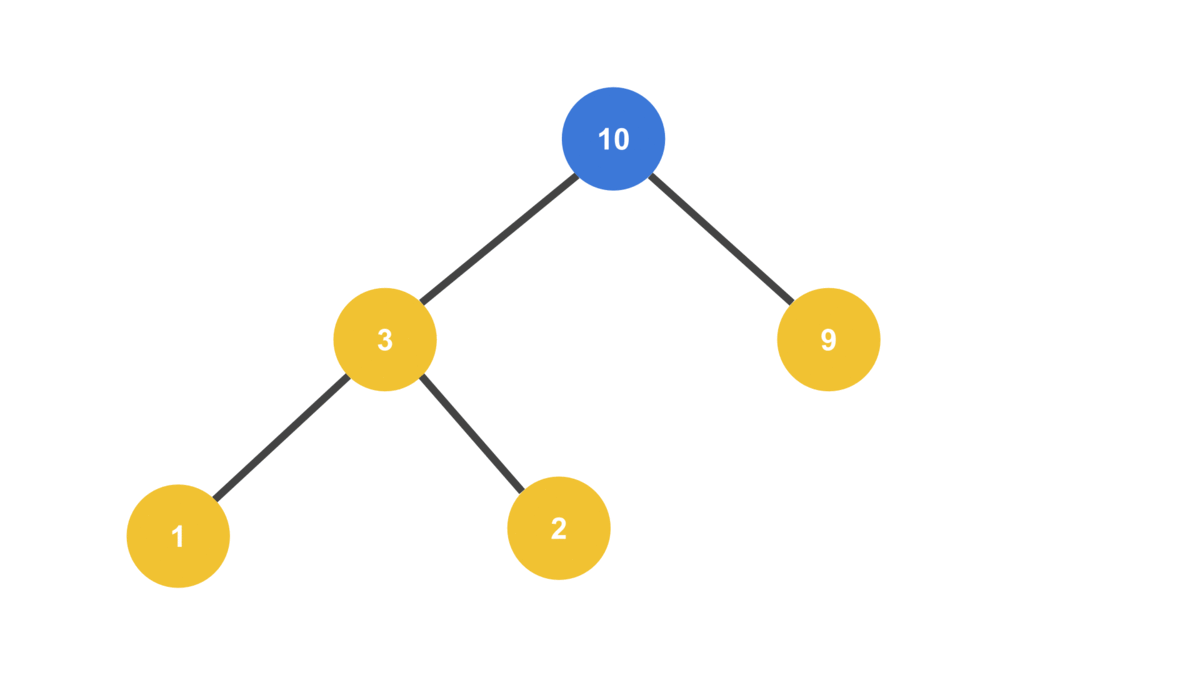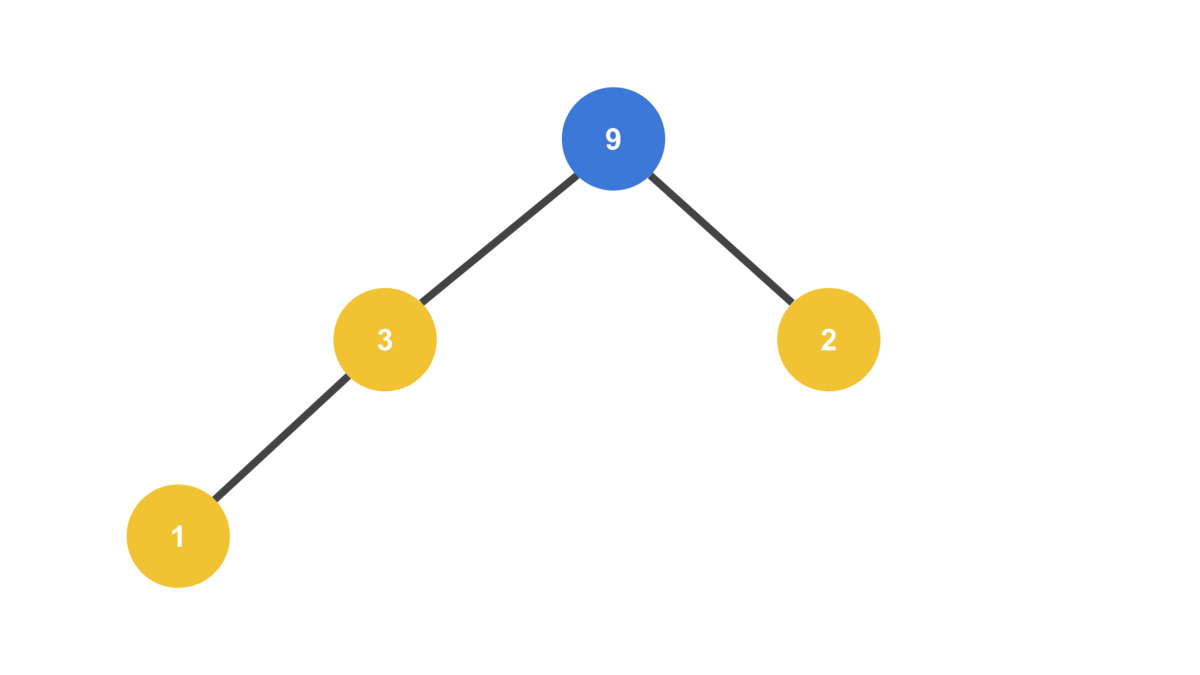
MAX_VALUE = 32
HEAP = [ 23, 10, 9, 1, 2, 3 ]

MAX_VALUE = 23
HEAP = [ 10, 3, 9, 1, 2 ]

MAX_VALUE = 10
HEAP = [ 9, 3, 2, 1 ]
...

트리의 맨 끝에서 노드를 빼와서 루트 노드로 사용한다는 것에 주의하자

마치며

힙 자체는 단순히 데이터들이 느슨하게 정렬되어있는 완전 이진 트리이지만, 루트에는 항상 힙 내부에 있는 데이터들의 최대 값과 최소 값이 위치한다는 특징 때문에 다양하게 응용하여 사용할 수 있다.

그 중 대표적인 것은 선형 자료 구조를 정렬할 때 사용하는 방법인데, 이 정렬 알고리즘을 힙 정렬(Heap Sort)라고 한다. 현재 V8의 Array.prototype.sort 메소드는 퀵 정렬(Quick Sort)을 사용하고 있지만, 초반에는 힙을 사용하는 정렬 알고리즘인 힙 정렬을 잠깐 사용하기도 했었다.

어쨌든 그 동안 잊고 있었던 기초적인 자료 구조를 한번 다시 보니 왠지 기분이 좋다.

힙은 굉장히 다양한 곳에서 사용되고 있는 자료 구조이니 만큼, 알고 있어서 나쁠 게 없기도 하고 면접 때도 꽤 자주 물어봤던 것 같다. 이제 필자는 회사의 비즈니스 로직과 전혀 관련 없는 백수 개발랭이 신분이 되었으니, 그 동안 소홀했던 기초 이론 부분을 이 기회에 조금 더 자세히 공부해봐야겠다.

이상으로 최소 값과 최대 값을 빠르게 찾을 수 있게 도와주는 힙(Heap) 포스팅을 마친다.