2019-07-14프로그래밍 / 알고리즘

컴퓨터가 만드는 랜덤은 정말로 랜덤할까?

이번 포스팅에서는 랜덤에 대해서 한번 이야기 해볼까 한다. 랜덤이란 어떤 사건이 발생했을 때 이전 사건과 다음 사건의 규칙성이 보이지 않는, 말 그대로 무작위로 발생하는 패턴을 이야기한다. 우리가 사용하고 있는 컴퓨터도 랜덤한 패턴을 만들어야 할 때가 있고 또 실제로도 만들고 있다.

하지만 컴퓨터는 사실 그냥 기능이 많은 계산기에 불과하다. 계산기는 입력된 값을 가지고 이리 저리 가지고 놀다가 결과값을 내놓는 물건이다. 근데 이런 계산기가 어떻게 랜덤한 결과를 만들어낼 수 있는 것일까? 우리는 이 질문에 대한 답을 찾기 전에 근본적으로 랜덤이란 것이 무엇인지부터 생각해봐야한다. 진짜 무작위라는 것이 존재하기는 하는 걸까?

랜덤(Random)이란 무엇일까?

먼저, 랜덤이란 무엇일까? 위에서 설명했듯이 무작위로 발생하는 어떠한 패턴이다.

사람마다 의견이 분분하겠지만 지금 필자 머리 속에 떠오른 대표적인 랜덤은 바로 도박이다. 도박의 가장 위험한 점이 비록 이번 판에는 잃었지만 다음 판에는 나도 딸 수 있을거야!라는 희망인데, 이런 희망은 도박할 때 사용하는 게임들이 랜덤에서 기반하는 게임이라는 생각에서 출발하기 때문이다. 즉, 어느 정도 운빨게임이어야 한다는 것이다.

대법원 판례 2006도736에도 도박의 정의를 재물을 걸고 우연에 의하여 재물의 득실을 결정하는 것이라고 이야기하고 있다. 대표적인 도박인 파칭코, 섰다, 포커, 주식 등만 살펴봐도 대충 감이 온다.

필자는 도박에서 사용하는 게임을 잘 모르기 때문에 누구나 해봤을 법한 가벼운 도박을 예로 들어보겠다. 필자가 중고등학생 시절을 보낸 2000년대에 전국의 중, 고등학교에서 널리 행해졌던 놀이인 판치기이다. 판치기는 워낙 전국적으로 유행했기 때문에 필자 또래의 독자분들이면 독자분들이면 한번 쯤은 해봤거나 아니면 친구들이 하는 걸 보기는 했을 거라 믿는다.

판치기하다가 선생님들한테 걸리면 교무실로 끌려가서 바로 빠따행이었다.

그래도 혹시 판치기가 뭔지 모르는 분들이 있을 수 있으니 일단 간단하게 룰을 설명하겠다.

적당히 두꺼운 교과서를 준비한다. 국사책이나 물리책처럼 적당히 두꺼운 책을 사용하자.

각자 준비한 동전을 교과서에 올린다. 보통 100원을 건다.

순서대로 교과서를 손으로 때려서 동전을 뒤집는다.

모든 동전을 뒤집어서 같은 면으로 만든 사람이 판돈을 모두 가져간다.

상식적으로 교과서를 손으로 때렸을 때 n개의 동전이 뒤집어 질 것이라는 계산을 하기란 쉽지 않다. 즉, 판치기는 어느 정도 랜덤에 기반한 게임이고 그래서 도박의 기본적인 특성인 사행성을 가질 수 있는 것이다.

참고로 형법 제 246조 1항과 국내 도박법 판례 상 학교에서 하는 판돈이 몇백원 정도인 판치기는 일시 오락으로 판정받아서 무죄이지만, 아무리 판치기라고 해도 몇백만원 수준의 돈이 왔다갔다 하는 수준이면 도박죄로 처벌받을 수 있다는 점 알아두자.(물론 저 정도 돈이 있는 사람들이면 판치기말고 다른 걸 한다…)

그럼 이 쯤에서 처음의 그 질문을 한번 던져보겠다.

이게 정말로 랜덤일까?

예전에 필자의 학창시절을 생각해봐도 학교에 1~2명씩 판치기의 절대 고수들이 있었는데 이 친구들은 자신이 원하는 동전만 정확히 뒤집을 수 있는 능력을 보유하고 있었다. 예전에 TV에서도 판치기의 고수라고 나온 분이 있었는데 이 분은 뭐 거의 닥터 스트레인지 수준이었다.

사실 판치기도 결국은 물리 법칙 내에서 돌아가는 판이기 때문에 판돈으로 걸린 동전의 무게, 판을 내려치는 힘, 판으로 사용된 교과서의 탄력성 등 몇가지 변수를 알면 어느 동전이 뒤집어 질지도 계산할 수 있을 것이다. 물론 이렇게 계산하는 것이 쉬운 일은 아니기 때문에 우리는 진정한 의미의 랜덤이 아니더라도 이 정도면 그냥 랜덤하다고 치는 것이다.

즉, 우리 주변에서도 진정한 의미의 랜덤은 그렇게 많지 않다는 것을 알 수 있다. 단지 우리가 랜덤하다고 생각할 뿐이다.

컴퓨터에서의 랜덤

사실 우리가 일상에서 어느 정도 우연성이 있다면 랜덤하다고 하듯이 컴퓨터도 진정한 의미의 랜덤을 만들어 내는 것이 아니라 어느 정도 납득할만한 우연성을 만들어 내고 이를 랜덤하다고 한다. 게다가 컴퓨터로 뭔가를 만드려면 어떠한 규칙을 만들어줘야 하는데, 어떠한 규칙으로 규칙이 없는 랜덤을 생성한다는 말 자체가 모순이다.

그래서 우리는 랜덤은 아니지만 랜덤에 가까운 유사 랜덤(Pseudo Random)밖에 만들 수 밖에 없는 것이다. 또한 컴퓨터는 기본적으로 숫자를 기반으로 하는 일종의 계산기이기 때문에 랜덤한 사건을 만들기 위해서는 난수, 즉 랜덤한 수를 뽑아 낼 수 있어야 한다.

그럼 컴퓨터는 어떻게 이런 난수 생성을 하는 걸까?

중앙제곱법(Mid Square Method)

중앙제곱법은 폰 노이만이 1949년에 고안한 유사 난수 생성법으로, 임의의 숫자를 제곱한 다음 이 숫자의 일부분을 가져와서 새로운 난수로 만들어내는 방법이다.

임의의 4자리 난수를 만든다고 가정해보자. 초기 값은 심플하게 1234로 가겠다.

페이즈	대상값	제곱값	난수
0	1234	1522756	1522756
1	5227	27321529	27321529
2	3215	10336225	10336225

이런 식으로 계속 중앙에 있는 값을 빼와서 제곱하면서 임의의 난수를 생성하는 방법이 바로 중앙제곱법이다. 뭔가 딱봐도 예측하기 쉬워보인다. 아무래도 폰 노이만 형이 활동하던 1950년대에 개발된 알고리즘이고, 그 당시 컴퓨터의 성능은 눈물나기 그지 없었으므로 최대한 간단한 방법을 사용한 것이다. 그래서 이 방법은 요즘에는 거의 사용되지 않는다.

선형합동법(Linear Congruential Method)

선형합동법은 C의 rand함수에서 사용하는 알고리즘이며 다음과 같은 재귀 관계식으로 정의되며 난수들의 수열을 반환한다.

X_{n+1} = (aX_n + c) \mod m

여기서 $X$ 는 난수로 된 수열이고 나머지는 그냥 임의의 정수이다. 참고로 ANSI C 표준은 $m = 2^{31}, a = 1103515245, c = 12345$ 로 정해져있다. 그럼 간단하게 한번 자바스크립트를 사용해서 구현해보자.

let m = 2 ** 31;
const a = 1103515245;
const c = 12345;

function rand (x) {
  return (((x * a) + c) % m);
}

function getRandomNumbers (randCount = 1) {
  // 현재 시각을 사용하여 초기값을 설정한다.
  const initial = new Date().getTime();

  const randomNumbers = [initial];
  for (let i = 0; i < randCount; i++) {
    randomNumbers.push(rand(randomNumbers[i]));
  }

  randomNumbers.shift();
  return randomNumbers;
}

console.log(getRandomNumbers(10));

코드를 브라우저 콘솔에 붙혀넣고 실행시켜보면 인자로 주었던 10만큼의 길이를 가진 난수 배열이 출력된다.

(10) [1163074432, 465823232, 1719475776, 1744670976, 790949120, 552540416, 896259328, 1473241344, 1074855168, 575793408]

선형합동법의 특징은 이전에 생성된 난수를 활용한다는 것이며 최대 $m$ 만큼 경우의 수를 가지므로 최악의 경우 $m$ 만큼의 반복 주기를 가진다. 필자가 m 변수를 let 키워드로 선언한 건 이 이유다. 한번 브라우저에서 m 변수에 작은 수를 할당한 다음에 getRandomNumbers 함수를 다시 호출해보자. 난수의 경우의 수와 동일한 값이 출현이 눈에 띄게 커진다는 것을 확인해볼 수 있다.

선형합동법은 계산이 굉장히 간단하고 빠르기 때문에 초창기부터 컴퓨터에 널리 사용되었다. 그러나 선형합동법은 난수에 주기성이 있고 생성되어 나오는 난수들 사이에 상관 관계가 존재하기 때문에 마지막으로 생성된 난수와 그 외 변수들만 알면 그 다음에 생성될 난수를 모두 예측할 수 있다.

문제는 그 변수들이 ANSI C 표준으로 정해져 있어서 누구든지 다 알 수 있다는 점이다. 즉, 조금 지식이 있는 사람이면 rand 함수의 결과를 보고 다음 난수를 미리 예상할 수 있다는 것이다.

그래서 이 알고리즘은 난수가 예측당해도 상관없는 경우나 임베디드처럼 메모리를 많이 사용하지 못하는 제한된 상황에서 주로 사용한다.

메르센 트위스터(Mersenne Twister)

메르센 트위스터는 엑셀, MATLAB, PHP, Python, R, C++ 등에서 사용하고 있는 난수 생성 알고리즘이며, 1997년에 마츠모토 마코토와 니시무라 다쿠지가 개발한 알고리즘이다. 메르센 트위스터라는 이름은 이 알고리즘의 난수 반복 주기가 메르센 소수인데서 유래했다.

메르센 소수라고 하면 뭔가 대단한 수 같은데 사실 별 거 없다. 메르센 수는 $M_n = 2^{n} - 1$ 으로 나타내며 식 그대로 2의 n제곱에서 1이 모자란 수를 말하는 것이고 메르센 소수는 그냥 이 메르센 수 중에서 소수인 것을 고른 것이다.

보통 $2^{19937} - 1$ 의 난수 반복 주기를 가지는 MT19937이 많이 사용되는데, C++에서도 이 알고리즘을 채택해서 사용하고 있다. 이 알고리즘의 동작 원리를 간단하게 설명하면 다음과 같다.

seed를 사용하여 624 만큼의 길이를 가진 벡터를 생성. seed는 보통 하드웨어 노이즈나 오늘 날짜를 사용한다.

이 벡터를 사용하여 624개의 유사 난수를 만든다.

이 벡터에 노이즈를 준 후 다시 2번을 반복. 이 노이즈를 주는 행위를 Twist한다고 한다.

이때 3번의 Twist하는 과정에서 GFSR(Generalized Feedback Shift Register라는 방법을 사용한다. GFSR은 자료가 많지 않고 대부분 논문같은 학술 자료만 있는 상황이라 필자가 자세히 알아보지는 못했으나, 열심히 구글링하고 논문들을 뜯어본 결과 LFSR(Linear Feedback Shift Register)를 약간 변형한 방법이라는 정보를 얻을 수 있었다. (정보가 너무 제한적이라 LFSR 기반이 맞는지는 정확하지 않다.)

LFSR은 이전 상태 값들을 가져와서 선형 함수를 통해 계산한 후 그걸 사용해서 다음 값을 만들어 내는 방법이다. 이때 사용하는 함수는 보통 XOR를 많이 사용하고 맨 처음 값을 시드(Seed)라고 부른다.

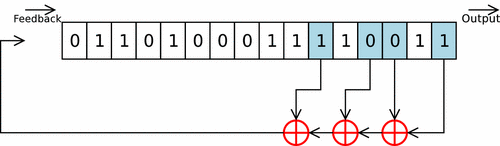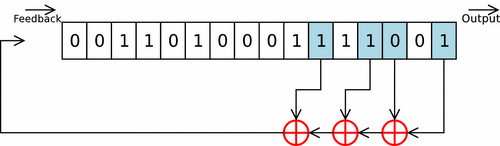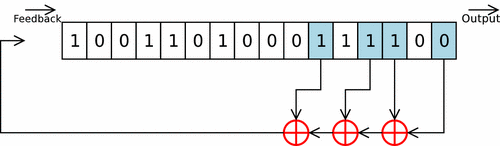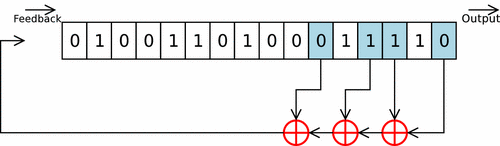
LFSR를 간단히 설명하자면, 우선 몇개의 메모리 주소를 골라놓고 초기화된 인풋인 시드를 레지스터에 밀어넣는다. 그러면 오른쪽으로 한칸씩 비트가 밀리게(Shifting) 된다. 그러면 우리는 끝에서 삐져나온 한개의 비트를 아웃풋에서 얻게 된다. 그 다음 미리 골라놨던 메모리 주소에 접근해서 값을 빼온 다음에 순서대로 하단에 위치한 3개의 XOR 게이트에 통과시키면 다음 인풋이 나오고 그걸 또 레지스터에 밀어넣는걸 반복하는 것이다.

메르센 트위스터도 결국은 LFSR가 약간 변형된 GFSR를 사용하여 난수를 생성하기 때문에 초반에 시드를 생성해줘야한다.

메르센 트위스터의 자세한 알고리즘은 위키피디아의 Mersenne Twister - Algorithmic_detail에서 확인할 수 있다. 필자는 2002년에 마츠모토 마코토와 니시무라 다쿠지가 자신들의 메르센 트위스터 알고리즘을 개선해서 다시 작성한 C의 MT19937 알고리즘 코드를 보고 자바스크립트로 한번 포팅해보았다. 이 코드는 최대 32bit 길이의 난수를 사용하도록 작성되어있다. 64bit용 알고리즘은 MT19937-64라고 또 따로 있다.

const N = 624;
const M = 397;
const F = 1812433253;

const UPPER_MASK = (2 ** 32) / 2; // 0x80000000
const LOWER_MASK = UPPER_MASK - 1; // 0x7fffffff
const MATRIX_A = 0x9908b0df;

class MersenneTwister {
  constructor () {
    const initSeed = new Date().getTime();
    this.mt = new Array(N);
    this.index = N + 1;

    this.seedMt(initSeed);
  }

  seedMt (seed) {
    let s;

    this.mt[0] = seed >>> 0;

    for (this.index = 1; this.index < N; this.index++) {
      this.mt[this.index] = F * (this.mt[this.index - 1] ^ (this.mt[this.index - 1]) >>> 30) + this.index;
      this.mt[this.index] &= 0xffffffff;
    }
  }

  int () {
    let y;
    const mag01 = new Array(0, MATRIX_A);
    if (this.index >= N) {
      let kk;

      if (this.index === N + 1) {
        this.seedMt(5489);
      }

      for (kk = 0; kk < N - M; kk++) {
        y = (this.mt[kk] & UPPER_MASK) | (this.mt[kk + 1] & LOWER_MASK);
        this.mt[kk] = this.mt[kk + M] ^ (y >>> 1) ^ mag01[y & 1];
      }

      for (; kk < N - 1; kk++) {
        y = (this.mt[kk] & UPPER_MASK) | (this.mt[kk + 1] & LOWER_MASK);
        this.mt[kk] = this.mt[kk + (M - N)] ^ (y >>> 1) ^ mag01[y & 1];
      }

      y = (this.mt[N - 1] & UPPER_MASK) | (this.mt[0] & LOWER_MASK);
      this.mt[N - 1] = this.mt[M - 1] ^ (y >>> 1) ^ mag01[y & 1];
      this.index = 0;
    }

    y = this.mt[this.index++];

    y ^= (y >>> 11);
    y ^= (y << 7) & 0x9d2c5680;
    y ^= (y << 15) & 0xefc60000;
    y ^= (y >>> 18);

    return y >>> 0;
  };
}

코드 내부에 사용된 상수 F = 1812433253, MATRIX_A = 0x9908b0df, this.seedMt(5489) 등은 필자가 임의로 넣은 수가 아니라 MT19937의 표준 계수로 정해져 있는 수이다.

사실 알고리즘 자체가 너무 복잡해서 필자도 다 이해하지는 못했다.(대학 때 공부를 열심히 안한 죄…) 그래도 일단 이렇게 코드로 한번 직접 작성해보면 글로만 읽을 때보다는 확실히 조금 더 이해가 되기 때문에 C로 작성된 원래 코드를 자바스크립트로 포팅한 것이다. 필자가 참고한 C 라이브러리 코드는 여기서 확인할 수 있다.

const rand = new MersenneTwister();
console.log(rand.int()); // 2145258025

작성한 코드를 직접 실행해보니 랜덤한 난수가 잘 생성이 되는 것 같다. 사실 난수가 잘 생성되는지 정확하게 보려면 결과를 시각화한 후 난수의 분포도를 봐야하지만 귀찮은 관계로 일단 패스하겠다. 참고로 이 알고리즘을 만든 마츠모토 마코토의 홈페이지에 들어가면 이 알고리즘이 왜 이런 이름을 가지게 되었는지 나와있다.

마코토: Knuth 교수님이 이 이름 발음하기 너무 힘들대.
다쿠지: …

[며칠 후]

마코토: 하이 타쿤, 메르센 트위스터는 어때? 메르센 소수를 사용하기도 했고, 원형은 Twisted GFSR(Generalized Feedback Shift Register)니까.
다쿠지: 글쎄…?
마코토: 왠지 제트코스터 같이 들리는 걸? 빨라보이기도 하고 기억하고 쉽고 발음하기 좋고. 그리고 이건 비밀인데 이 이름엔 우리들의 이니셜이 숨어있지!(Makoto, Takuji)
다쿠지: …
마코토: 자자자 MT로 가는거다?
다쿠지: 음…그래

나중에 우리는 Knuth 교수님으로부터 “좋은 이름인 것 같다”라는 편지를 받았다.

뭔가 깨발랄한 마코토형과 시니컬한 다쿠지형 케미가 돋보인다. 뭔가 이런 대단한 알고리즘을 개발한 사람이지만 사람 냄새나는 네이밍 과정인듯.

XOR 시프트(XOR shift)

XOR 시프트도 메르센 트위스터와 마찬가지로 Linear Feedback Shift Register을 기반으로 한 의사 난수 알고리즘이다. 어떻게 보면 메르센 트위스트의 하위호환이라고 볼 수도 있는데, 메르센 트위스트와 원리는 비슷하지만 구현이 훨씬 간단하고 작동이 빠르기 때문에 왕왕 사용된다.

XOR 시프트 알고리즘은 여러 종류가 있는데, 32bit, 64bit, 128bit의 수를 사용하며 각각 $2^{32} -1$ , $2^{64} - 1$ , $2^{128} - 1$ 의 메르센 수 난수 반복 주기를 가진다.

근데 이게 TestU01이라는 난수 품질 테스트 프레임워크의 테스트를 통과하지 못해서 조금 문제가 있었다. 이걸 통과해야 ANSI C 표준이 될 수 있기 때문이다.

그래서 몇가지 변종 알고리즘이 나오게 되었는데 그 중 하나가 128bit를 사용하는 XOR 시프트 128을 개량한 XOR 시프트 128 +라는 알고리즘이다.(뭔가 게임 후속작 제목 같다…)

참고로 V8, SpdierMonkey, JavaScriptCore 등 메이저 자바스크립트 엔진들이 채택한 난수 생성 알고리즘이 XOR 시프트 128 +이다. 이 알고리즘은 2016년 11월에 Sebastiano Vigna라는 분에 의해 학회에서 발표되었다. 논문 내용은 여기에서 확인할 수 있다.

전반적인 원리는 위에서 설명한 LFSR와 비슷하니, V8엔진에서 Math.random 메소드를 어떻게 구현했는지 한번 살펴보자. 원래 코드는 C++로 작성되어있으나 여러분이 브라우저에서 코드를 쉽게 실행시켜볼 수 있도록 동일한 로직을 자바스크립트로 포팅해서 작성하겠다.

V8 내부 소스 코드는 v8/src/base/utils/random-number-generator.h의 XorShift128 메소드에 작성되어 있다.

// xorshift128plus.js
const state = [1827981275, 1295982171];

function xorshift128plus () {
  let s1 = state[0];
  let s0 = state[1];

  state[0] = s0;
  s1 ^= s1 << 23;
  s1 ^= s1 >> 17;
  s1 ^= s0;
  state[1] = s1;
  console.log('레지스터의 현재 상태 -> ', state);
  return state[0] + state[1];
}

console.log('초기 레지스터 상태 -> ', state);
for (let i = 0; i < 5; i++) {
  console.log('난수 -> ', xorshift128plus());
}

초기 레지스터 상태 ->  [ 1827981275, 1295982171 ]
레지스터의 현재 상태 ->  [ 1295982171, 867440954 ]
난수 ->  2163423125
레지스터의 현재 상태 ->  [ 867440954, 1393243966 ]
난수 ->  2260684920
레지스터의 현재 상태 ->  [ 1393243966, 37812574 ]
난수 ->  1431056540
레지스터의 현재 상태 ->  [ 37812574, 833890405 ]
난수 ->  871702979
레지스터의 현재 상태 ->  [ 833890405, 1661667227 ]
난수 ->  2495557632

출력된 로그를 보면 레지스터의 상태가 어떻게 변하고 있는지 알 수 있다.

[1]번 인덱스에 있던 값이 [0]번 인덱스로 옮겨지고 [1]번 인덱스에 새로운 난수를 꽂아넣은 후 두 원소를 더해서 출력하고 있다는 걸 알 수 있다.

계산 과정을 보면 [1]번 인덱스에 새로운 값을 넣을 때는 시프팅되어 왼쪽으로 삐져나온 값인 [0]번 인덱스의 값을 사용하여 XOR 시프팅을 진행하고 그 값을 다시 [1]번 인덱스에 넣어준다.

그리고 시프팅하는 상수인 23, 17은 XOR 시프팅 128+ 알고리즘을 개발할 때 연구를 통해 찾아낸 최적의 상수이기 때문에 사용하는 것이다. 해당 논문을 보면 뭐 이것저것 시도해본 다음에 결과를 일일히 테스트해서 나온 결과를 비교한 도표도 함께 첨부되어있다.

마치며

사실 처음에는 가벼운 마음으로 랜덤에 대한 이야기를 해보려고 했는데 예상보다 수학적인 내용이 많이 나와서 왠지 어려운 포스팅이 되어버린 것 같다.

사실 컴퓨터라는 계산기로 진정한 의미의 난수를 만드는 것은 거의 불가능하다. 최근에 미국에서 양자컴퓨터를 사용해서 진정한 의미의 난수를 생성하는 데 성공했다고 하지만 양자컴퓨터는 아직은 우리와 너무나도 먼 이야기이기 때문에 논외로 치겠다.

필자도 사실 수학을 그다지 좋아하는 편은 아니다. 하지만 이렇게 수학적인 연구를 통해 생성 규칙이 없는 난수를 만드려는 많은 사람들의 도전을 보면, 편하게 상위 레이어에서 코딩하고 있는 필자로써는 이 분들에게 굉장히 감사함을 느낀다.(난 안될꺼야 아마…)

연구원 분들이 기반 알고리즘을 만들어주시면 열심히 상용 어플리케이션에 써먹겠습니다...!!!

필자는 이 포스팅을 작성하면서 논문과 위키피디아를 엄청 들여다봤는데 오랜만에 영어와 수식을 너무 많이 봐서 머리에 과부하가 걸린 상태다. 그리고 다른 건 몰라도 메르센 트위스트 같은 경우는… 아니 너무 복잡하다 인간적으로…

참고로 이거 만든 마츠모토 마코토님은 지금 히로시마 대학교의 수학 대학원에서 조교수로 근무하고 계신데, 이 정도 머리가 되야 강단에 설 수 있는 건가라는 생각도 든다. 완전 어나더레벨…

이상으로 컴퓨터가 만드는 랜덤은 정말로 랜덤할까? 포스팅을 마친다.

참고문헌

XorShift - Wikipedia
There’s Math.random(), and then There’s Math.random() - V8 Dev
Futher scramblings of Marsaglia’s xorshift generators - Sebastiano Vigna
The Xorshit128+ random number generator fails BigCrush - Daniel Lemire