[JavaScript로 천체 구현하기] 행성의 움직임을 구현해보자

케플러 방정식을 활용한 천체 시뮬레이션 구현

May 03, 2017

이번 포스팅에서는 저번 포스팅에 이어 실제 궤도의 모양과 크기, 위치, 방향을 정의하고 코드로 작성을 해보려고 한다.

케플러 궤도 요소 데이터 확인하기

어떤 천체든 케플러 궤도 요소를 사용하여 궤도를 구하는 방법은 동일하니, 이 포스팅에서는 우리에게 가장 익숙한 지구의 궤도를 한번 구해보도록 하자.

NASA의 제트 추진 연구소 사이트(JPL)에서는 태양계 내 행성들의 케플러 궤도 요소 데이터를 제공하는데, 필자도 이 데이터를 그대로 사용하여 지구의 궤도를 구해볼 예정이다.

JPL이 제공하는 궤도 데이터는 크게 세 가지인데, 이 데이터들은 계산의 목적이나 정밀도에 따라 용도가 다르다.

Table 1: 평균 황도와 춘분점을 기준으로 한 케플러 궤도 요소와 변화율. 서기 1800년 - 2050년 사이의 예측에 유효하며, 장기적인 궤도 요소 변화는 무시하지만 계산이 단순하고 빠름.
Table 2a: Table 1과 동일한 기준으로 측정했지만, 기원전 3000년 - 서기 3000년 사이의 예측에 유효하다. 다만 더 넓은 시간 범위를 다루기 때문에 목성에서 해왕성까지의 궤도 계산에는 반드시 Table 2b의 추가 항을 적용해야한다.
Table 2b: Table 2a에서 다루는 목성, 토성, 천왕성, 해왕성의 궤도 계산에 필요한 평균 근점 이각 계산을 보정하는 항이다. 이 항들은 중력 교란이나 천체 간 상호작용, 일반 상대성 효과 등을 반영했다.

이 중 Table 2a와 Table 2b의 데이터는 궤도에 대한 우주 탐사 등에 필요한 고정밀 계산에 사용하는 데이터인데, 특히 목성처럼 질량이 어마무시한 행성은 다른 천체에 미치는 중력 효과가 크기 때문에 별도의 보정 값을 통해 정밀도를 높여줘야 한다.

어차피 필자가 하려고 하는 계산은 단순한 시뮬레이션이라 고정밀 계산이 필요한 영역은 아니기 때문에 Table 1에서 주어진 요소만으로도 충분히 계산이 가능하다.

궤도 요소 데이터 살펴보기

Table 1은 역기점인 J2000, 즉 2000년 1월 1일 정오에 측정한 궤플러 궤도 요소 값, 그리고 한 세기 동안 궤도 요소가 변화한 변화량을 의미한다. 이 테이블에서 주어진 궤도 요소 데이터는 아래와 같다.

semi-major axis(a): 장반경. 단위는 AU이다.
eccentricity(e): 이심률. 단위는 Radian이다.
inclination(I): 기울기. 단위는 Degree이다.
mean longitude(L): 평균 경도. 단위는 Degree이다.
longitude of perihelion(long.peri.): 근일점 경도. 단위는 Degree이다.
longitude of the ascending node(long.node): 승교점 경도. 단위는 Degree이다.

JPL은 태양계 행성에 대한 모든 데이터를 제공하지만, 이 포스팅은 궤도 계산 과정을 간단하게 설명하기 위한 포스팅이니, 지구의 궤도 요소인 EM Bary라고 적혀있는 로우만 확인하면 된다. (EM Bary는 지구와 달 간의 질량 중심을 의미한다. Earth/Moon Barycenter의 줄임말이다.)

그럼 Table 1의 지구 궤도 요소를 한번 살펴보도록 하자. 이 데이터는 크게 J2000 기점으로 측정한 데이터와 한 세기 동안 궤도 요소의 변화량으로 나누어진다.

J2000 기점으로 측정한 궤도 요소

J2000은 율리우스력으로 2000년 1월 1일 정오를 의미한다. 이렇게 행성 궤도 요소의 기준이 되는 관측이 실시된 시기를 역기점(曆起點)이라고 한다.

a	e	I	L	long.peri.	long.node
1.00000261	0.01671123	-0.00001531	100.46457166	102.93768193	0.0

한 세기 동안의 궤도 요소 변화량

이 값들은 한 세기 동안 궤도 요소가 변화한 값을 의미한다. 이 값들을 이용하면 현재 이 포스팅을 작성하고 있는 2017년 5월 3일 22시 27분의 지구 궤도 요소가 어떤 상태인지 구해볼 수 있다.

a	e	I	L	long.peri.	long.node
0.00000562	-0.00004392	-0.01294668	35999.37244981	0.32327364	0.0

이제 이 값들을 토대로 해서 현재 지구가 궤도 상 어디쯤에 위치해있는지를 계산해보자.

현재 시점의 지구 궤도와 위치를 알아보자

위 데이터를 살펴보면 이전 포스팅에서 설명했던 케플러 궤도 요소 중 근일점 편각과 근일점 통과 시각이 없는 것을 볼 수 있지만, 큰 문제는 없다.

우선 근일점 편각의 경우 결국 근일점이 승교점으로부터 얼마나 떨어져있는지를 의미하는 것이니 이미 주어진 근일점 경도와 승교점 경도만으로도 충분히 계산이 가능하다. 하지만 이 포스팅에서는 2차원의 궤도 평면 상에서의 행성 위치만 구할 것이기 때문에 궤도의 포지션을 결정할 때 필요한 근일점 편각은 계산할 필요가 없다.

또한 근일점 통과 시각은 결국 특정 시간을 기점으로 행성이 어디에 위치해있는지를 알아내기 위한 시간 개념인데, JPL 데이터는 J2000에 측정된 값과 한 세기 동안의 변화량을 함께 알려주고 있으므로 시간의 흐름에 따른 궤도 요소의 변화 또한 충분히 표현되고 있다.

태양을 중심으로 공전하는 행성의 위치를 계산하는 방법의 포인트는 결국 궤도 요소를 기반으로 평균 근점 이각( $M$ )과 편심이각( $E$ )를 계산한 뒤, 궤도 평면 상에서의 $x$ , $y$ 좌표를 구하는 것이다.

이때 $z$ 좌표를 고려하지 않는 이유는 어차피 궤도 평면 상에서의 행성 위치를 구한 뒤 궤도의 기울기( $I$ )와 승교점 경도( $\Omega$ ), 근일점 편각( $\omega$ )을 고려하여 3차원 공간에 궤도를 배치해주면 자연스럽게 3차원 공간에서의 행성 위치도 따라오기 때문이다.

결국 위에서 주어진 데이터를 토대로 평균 근점 이각과 편심이각을 구할 수 있냐는 것이 중요한데, 앞서 언급했듯이 이미 주어진 값들로도 충분히 계산이 가능하기 때문에 큰 문제는 없다.

그럼 본격적으로 한번 궤도 요소를 구해보도록 하자.

현재 시점의 지구 궤도 요소 계산하기

앞서 언급했듯이 JPL에서 가져온 데이터는 J2000 기준으로 측정한 궤도 요소 값과 한 세기 동안의 궤도 요소 변화량이다.

그렇기 때문에 현재의 궤도 요소 값을 알아내려면 J2000으로부터 현재까지 몇 세기가 지났는지를 알아낸 후, 한 세기 동안의 변화량에 해당 값을 곱해서 최종 궤도 요소 값을 보정해줘야 한다.

계산을 쉽게 하기 위해 각 시간 단위들을 원하는대로 변경할 수 있는 함수들을 먼저 선언해주도록 하자.

const DAY = 60 * 60 * 24;
const YEAR = 365.25; // 율리우스력은 1년을 365.25일로 정의한다

const convertMillisecondsToSeconds = (milliseconds: number) => milliseconds / 1000;
const convertSecondsToDays = (seconds: number) => seconds / DAY;
const convertDaysToYears = (days: number) => days / YEAR;
const convertYearsToCenturies = (years: number) => years / 100;

이제 역기점인 J2000으로부터 현재까지 몇 세기가 지났는지를 확인해보면 된다.

const J2000 = new Date('2000-01-01T12:00:00-00:00');
const now = new Date('2017-05-03T22:27:00-00:00');

const epochTime = convertMillisecondsToSeconds(
    today.getTime() - J2000.getTime()
  );
// Date객체끼리 연산하면 값이 ms로 나오기 때문에 1000으로 나눠서 초 단위로 나오게끔 환산해준다
// 결과: 547,122,420초

const centuries = 
  convertYearsToCenturies(
    convertDaysToYears(
      convertSecondsToDays(epochTime)
    )
  );
// 결과: 0.17337263289984028세기

결과적으로 J2000부터 현재까지는 약 6,332.43일이 지났으며, 이를 세기로 환산해보면 약 0.1734세기가 지났다는 사실을 알 수 있다. 이제 역기점으로부터 몇 세기가 지났는지 알았으니 JPL에서 가져온 궤도 요소를 선언하고 현재 시점의 지구 궤도 요소를 계산해보도록 하자.

필자는 앞으로의 계산을 용이하게 하기 위해 해당 데이터의 AU 단위를 모두 km로 환산하려고 한다. 1AU는 태양과 지구 간의 평균 거리를 의미하며 약 149,597,870km 이다.

interface KeplerOrbitElement {
  장반경: number;
  이심률: number;
  기울기: number;
  승교점경도: number;
  평균경도: number;
  근일점경도: number;
}

interface JPLOrbitElementData {
  J2000: KeplerOrbitElement;
  한세기변화량: KeplerOrbitElement;
}

const AU = 149597870;
const convertAUtoKM = (au: number) => au * 149_597_870;

const 지구_궤도요소: JPLOrbitElementData = {
  J2000: {
    장반경: convertAUtoKM(1.00000261), // 149598260.45044068km
    이심률: 0.01671123,
    기울기: -0.00001531,
    승교점경도: 0.0,
    평균경도: 100.46457166,
    근일점경도: 102.93768193
  },
  한세기변화량: {
    장반경: convertAUtoKM(0.00000562), // 840.7400294km
    이심률: -0.00004392,
    기울기: -0.01294668,
    승교점경도: 0.0,
    평균경도: 35999.37244981,
    근일점경도: 0.32327364
  }
};

궤도 요소의 선언이 끝났다면 이제 계산을 해볼 차례이다. 객체 프로퍼티에 대한 매핑 연산을 쉽게하기 위해 추상화된 mapValues 함수를 사용하면 간단하게 표현할 수 있다.

const 현재궤도요소 = mapValues(지구_궤도요소.J2000, (element, key) => {
  return element + (지구_궤도요소.한세기변화량[key] * centuries);
});
/**
  {
    장반경: 149598406.21175316,
    이심률: 0.01670361547396304,
    기울기: -0.0022599099989117043,
    승교점경도: 0,
    평균경도: 6341.770556025533,
    근일점경도: 102.99372873211391
  } 
 */

이렇게 간단한 과정을 통해 2017년 5월 3일 22시 27분의 지구 궤도 요소의 상태를 구해볼 수 있었다. 이제 이 값들을 사용하여 본격적으로 지구가 궤도 상 어디에 위치해있는지를 구해보도록 하자.

지구는 궤도의 어디쯤에 위치해있을까?

앞서 언급했듯이 케플러 궤도 요소를 사용한 궤도 계산의 포인트는 평균 근점 이각과 편심 이각을 구하고, 이를 토대로 궤도 평면 상에서 행성의 위치를 $x$ 와 $y$ 좌표로 나타내는 것이다. 이제 이 값들을 구해보면서 왜 궤도 계산에 이러한 값들이 필요한 것인지도 한번 살펴보도록 하겠다.

평균 근점 이각 구하기

평균 근점 이각은 고전 이체 문제에서 타원 궤도 상의 물체의 위치를 계산하기 사용하는 각도이다.

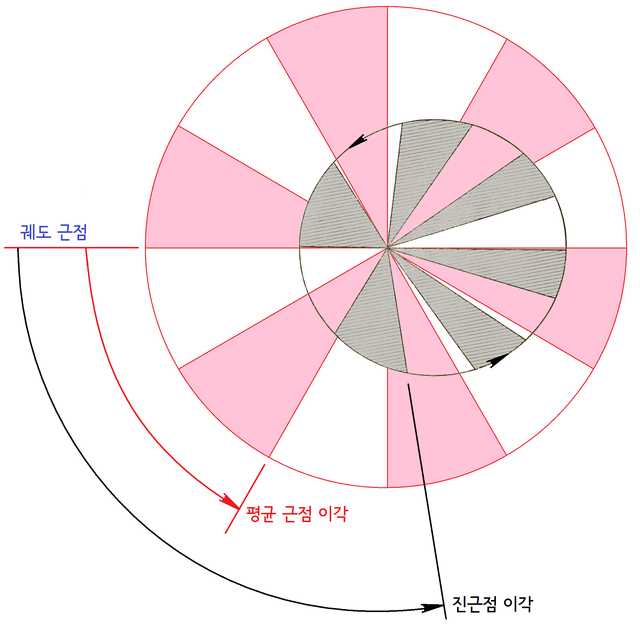
위 그림은 행성이 궤도를 따라 운동할 때 같은 시간동안 쓸고 지나간 면적을 보여주고 있다. 이때 회색 궤도의 면적은 조금씩 다른데 반해 분홍색 궤도의 면적은 동일한 것을 볼 수 있다.

기본적으로 타원 궤도를 도는 행성은 케플러 제2법칙인 면적속도 일정에 따라 비선형적인 움직임을 보인다. 즉, 근일점 근처에서는 행성의 운동 속도가 빨라지고 원일점 근처에서는 느려진다는 것이다.

이때 평균 근점 이각은 어떤 물체가 공전 속도와 공전 주기를 유지한 채 정확한 원 궤도로 옮겨간다고 가정했을 때의 물체와 근일점간의 각거리를 의미한다. 이렇게 궤도를 원에 가까운 형태로 단순화하면 궤도 상 행성의 위치를 표현하는 각도도 시간에 대해 선형적으로 증가하기 때문에 계산이 단순해지는 것이다.

물론 행성의 궤도 이심률이 0이라 완벽한 원이라면 실제 행성도 이렇게 움직이겠지만, 대부분의 궤도는 타원 형태이기 때문에 평균 근점 이각과 이심률을 사용하여 계산을 다시 보정하고 실제 행성의 움직임을 알아내는 과정을 거칠 것이다.

이처럼 평균 근점 이각은 궤도 상의 행성 위치를 계산하기 위한 가장 기본적인 재료로 사용된다. 평균 근점 이각을 구하는 방법은 여러가지가 있지만 이미 필자는 평균 경도와 근일점 경도를 알고 있기 때문에 이 값들을 사용하여 평균 근점 이각을 구할 것이다.

평균 경도( $l$ )과 근일점 경도( $\omega$ )로 평균 근점 이각을 구하는 공식은 아래와 같다.

M = l - \omega

const 평균근점이각 = 현재궤도요소.평균경도 - 현재궤도요소.근일점경도;
// 6238.776827293419도

이 원리를 이해하려면 평균 경도가 무엇인지에 대한 이해가 조금 더 필요한데, 계산에 사용된 평균 경도는 춘분점을 기준으로 행성이 궤도 상에서 얼마나 진행했는지를 평균적으로 나타내는 값이다. 평균 경도( $l$ )는 아래와 같은 수식으로 표현할 수 있다.

l = \frac{2\pi}{P}(t - T_0) + \varpi

$\frac{2\pi}{P}$ : 평균 운동(행성이 공전 궤도를 한 바퀴 도는데 걸리는 시간 $P$ ). 이는 행성이 궤도 상에서 운동하는 총 각도인 360도, 즉 $2\pi$ 라디안을 행성의 공전 주기로 나눠준 것이다.
$(t - T_0)$ : 기준 시점 $T_0$ 로부터 경과한 시간. 이때 기준 시점 $T_0$ 는 역기점 J2000이다.
$\omega$ : 근일점 경도.

이때 이 수식의 모양을 보면 $t - T_0$ 가 0인 경우 $l = \omega$ , 평균 경도와 근일점 경도가 같다는 결론이 도출되는데, 이를 통해 $\frac{2\pi}{P}(t - T_0)$ 라는 수식이 근일점을 기준으로 행성이 평균적으로 이동한 각도를 나타낸다는 것을 알 수 있다.

그래서 마지막으로 근일점 경도( $\omega$ )를 더해줌으로써 평균 경도의 기준점을 춘분점으로부터의 각도로 변경해주는 것이다.

하지만 우리에게 필요한 평균 근점 이각은 이름에서 알 수 있듯이, 춘분점이 아닌 근일점을 기준으로 잡는 값이다. 그래서 평균 경도에서 다시 근일점 경도를 다시 빼줌으로써 각도의 기준을 다시 근일점으로 만들어주는 것이다.

편심 이각 구하기

이렇게 평균 근점 이각을 통해 행성이 궤도 상의 근일점을 기준으로 얼마나 이동했는지를 구했다면 이제는 편심 이각(Eccentric anomaly)을 구할 차례이다.

앞서 구했던 평균 근점 이각은 마치 시간을 일정한 속도로 돌리는 시계와 같다. 이제 시간이 $t$ 만큼 흘렀으니 행성도 각도 $M$ 만큼 이동했을 것이라고 단순하게 계산하는 것이다.

하지만 실제로 타원 궤도를 도는 행성의 속도는 중심체와의 거리에 따라 비선형적으로 달라진다. 그래서 우리는 평균 근점 이각과 이심률을 사용하여 편심 이각이라는 값을 구함으로써 빨라졌다가 느려졌다가 하는 행성의 비선형적인 운동을 반영하여 정확한 위치를 알아내어야 한다.

편심 이각은 실제 타원 궤도의 행성 위치를 단순화하기 위해 정의된 각도이며, 실제 타원 궤도의 장반경을 반지름으로 가지는 가상의 원 궤도에 행성의 위치를 투영했을 때의 중심각을 의미한다. 그림으로 보면 더 직관적으로 이해하기가 쉽다.

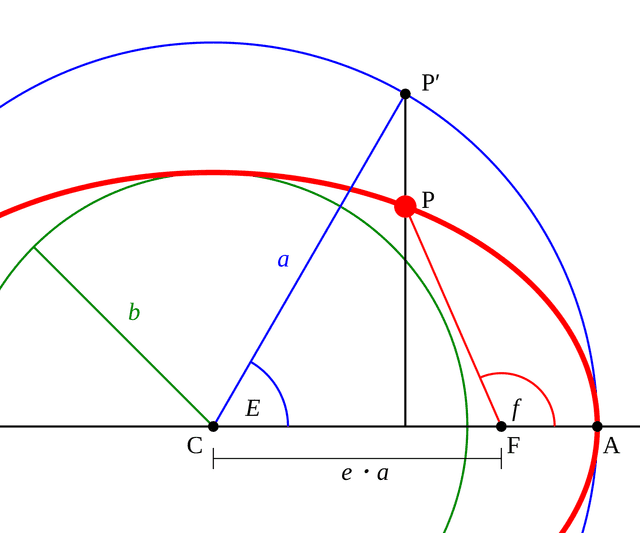
위 그림에서 $P$ 는 궤도 상 행성의 위치를 나타내며, $P'$ 는 실제 궤도의 장반경인 $a$ 를 반지름으로 가지는 가상의 원 궤도에 투영된 행성의 위치를 나타낸다.

이때 실제 궤도인 타원의 중심은 $C$ , 타원의 초점은 $F$ 로 나타내고 있다. 이때 타원의 초점은 궤도의 중력 중심을 의미하며, 태양계로 치면 태양이 될 것이다. 그리고 편심 이각 $E$ 는 타원의 중심인 $C$ 부터 가상의 원 궤도에 투영된 행성의 위치인 $P'$ 까지의 각도를 의미한다.

편심 이각도 평균 근점 이각과 마찬가지로 가상의 원 궤도에 반영된 행성 위치를 표현한 각도이지만, 편심 이각 계산에는 이심률이 사용되므로 평균 근점 이각과는 다르게 타원 궤도의 기하학적인 특성이 반영되어 비선형적인 증가율을 보이게 된다.

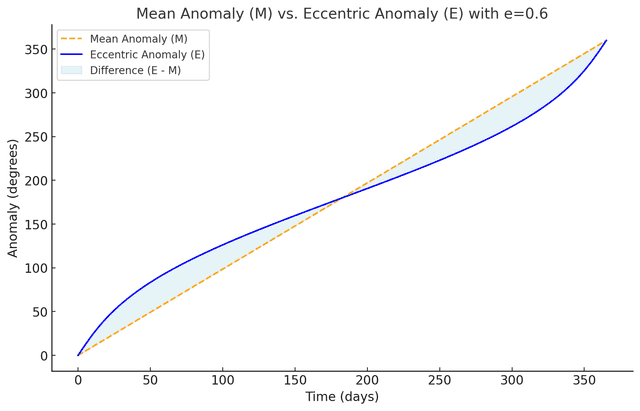JPL의 지구 궤도 요소 중 이심률을 0.6으로 변경한 뒤 계산한 평균 근점 이각과 편심 이각의 변화.
근일점인 0일에는 차이가 적지만 원일점인 180일에 가까울수록 차이가 커지는 모습을 볼 수 있다.

그리고 편심 이각을 구하면 최종적으로 중력 중심체의 위치인 $F$ 부터 실제 행성의 위치인 $P$ 까지의 거리, 그리고 각도 $f$ 인 진근점이각을 알아낼 수 있다.

평균근점이각과 마찬가지로 편심이각도 여러 개의 정의로 나타내어질 수 있는데, 필자는 이미 평균근점이각을 구했기 때문에 평균근점이각으로부터 유도되는 공식을 사용하겠다.

E = \frac{M+e \sin M}{1-e \cos M}

위 공식은 평균 근점 이각( $M$ )과 타원의 이심률( $e$ )를 사용해 편심 이각을 계산하고 있다. 이때 행성의 운동이 가지는 비선형적 특성은 이심률이 클수록 강해지는데, 이를 $e \sin M$ 과 $e \cos M$ 항을 통해 반영해주는 것이다.

이때 $e \sin M$ 은 타원의 비선형 운동에 맞춰 평균 근점 이각을 보정하고, $e \cos M$ 은 행성의 위치가 근일점과 원일점 어느 곳에 가까운지를 나타내는 정규화 인자 역할을 한다.

만약 $e = 0$ 이라면 궤도는 완벽한 원이 될테니 $E = M$ 이라는 공식이 성립하겠지만, $e > 0$ 라서 궤도가 타원일 경우 근일점 근처에서는 $e \sin M$ 과 $e \cos M$ 이 작아져 $E$ 와 $M$ 의 차이도 작아지고, 원일점 근처에서는 두 값이 커져 $E$ 와 $M$ 간의 차이가 커진다.

하지만 안타깝게도 편심 이각을 구하는 공식은 비선형 방정식이라 정확한 해가 아닌 근사값을 뱉어내기 때문에 뉴턴-랩슨 메소드를 사용하여 오차를 줄여줘야한다.

E_{n+1} = E_n - \frac{E_n - e \sin E_n - M}{1 - e \cos E_n}

자, 그럼 편심 이각을 구하는 방법을 알았으니 본격적인 계산을 진행해보자. JavaScript의 Math.sin, Math.cos와 같은 삼각함수 메소드들은 인자로 Degree 단위가 아닌 Radian 단위를 받기 때문에 계산에 사용할 평균 근점 이각을 Radian 단위로 변경해주어야 한다.

const convertDegreeToRadian = (degree: number) => degree * (Math.PI / 180);
const 평균근점이각 = convertDegreeToRadian(현재궤도요소.평균경도 - 현재궤도요소.근일점경도);

이후 반복 계산을 도와줄 뉴턴-랩슨 메소드 함수와 편심이각을 구하는 함수를 선언하고 6회 반복 계산해준다.

function 뉴턴랩슨메소드<T>(callback: (...args: T[]) => T, 초기값: T, 계산횟수: number) {
  let x = 초기값;
  let x1 = 초기값;
  
  for(let i = 0; i < 계산횟수; i++) {
    x = x1;
    x1 = callback(x);
  }

  return x1;
}

function get편심이각(이심률: number, 평균근점이각: number) {
  return (편심이각: number) => {
    return 편심이각 + (평균근점이각 + 이심률 * Math.sin(편심이각) - 편심이각) / (1 - 이심률 * Math.cos(편심이각));
  };
}

const 편심이각 = 뉴턴랩슨메소드(get편심이각(현재궤도요소.이심률, 평균근점이각), 평균근점이각, 6);
// 108.9017193604219라디안

이때 이심률이 클수록 get편심이각 함수가 뱉는 결과값의 오차도 크기 때문에 더 많은 횟수를 반복 계산해주어야 한다. 하지만 이 포스팅에서 예시로 사용하고 있는 지구 궤도의 이심률은 약 0.02 정도로 원에 가깝기 때문에 6회 정도만 계산을 진행해준 것이다.

이렇게 편심 이각을 구했다면 이제 지금까지 모은 재료들을 토대로 궤도 평면 상에 위치한 행성의 진짜 위치를 밝혀낼 차례이다.

궤도 평면 상의 행성 x, y 좌표 구하기

이제는 궤도 평면 상에서 행성이 어디에 위치한 것인지를 알아내어 $x$ 와 $y$ 좌표로 표현할 차례이다. 지금 구하는 좌표들은 타원의 중심을 기준으로 하는 좌표들이지만, 최종적으로 이 좌표들을 이용하여 지구가 태양을 기준으로 얼마나 멀리 떨어져있는지, 그리고 근일점을 기준으로 몇 도나 돌아간 곳에 위치한 것인지를 알아낼 것이다.

먼저 타원의 중심을 기준으로 행성의 $x$ 좌표를 구하는 공식은 아래와 같다.

x = a \cdot (\cos E - e)

편심 이각은 타원의 복잡한 비율을 반영하기 어렵기 때문에 가상의 원 궤도에 투영된 행성의 위치를 나타내는 값이다. 그래서 편심 이각을 사용하여 실제 타원 궤도에 위치한 행성의 위치를 구할 때는 가상의 원 궤도와 실제 타원 궤도 간의 차이를 보정해주게 된다.

$x$ 좌표를 구하는 공식의 $\cos E - e$ 항이 이 보정을 수행하는 과정이다. $\cos E$ 는 편심 이각( $E$ )를 기준으로 행성이 가상의 원 궤도에서 수평 방향으로 얼마나 떨어져 있는지를 계산한다. 이후 이심률 $e$ 를 빼줌으로써 최종 값은 타원의 중심과 초점 사이의 거리만큼 이동하게 되는 것이다.

여기까지 계산한 값은 그저 타원의 장반경에 대한 비율인 무차원값이기 때문에 최종적으로 장반경( $a$ )를 곱해줌으로서 궤도의 스케일을 확정해준다.

$y$ 좌표를 구하는 공식도 원리는 비슷하다.

y = a \cdot \sqrt{1 - e^2} \cdot \sin E

$y$ 좌표 또한 $\sin E$ 를 통해 가상의 원 궤도에서 행성이 수직 방향으로 얼마나 떨어져 있는지를 먼저 계산하고, 이후 가상의 원 궤도와 실제 타원 궤도와의 차이를 보정하는 방법을 사용한다.

다만 이때는 타원의 수직 방향으로의 보정이 필요하기 때문에 장반경이 아닌 단반경을 사용해야하는데, 위 공식의 $a \cdot \sqrt{1 - e^2}$ 가 바로 장반경과 이심률을 사용하여 단반경을 구하는 공식이다.

대략의 원리를 알았다면 이제 코드를 작성하고 지구의 좌표를 뽑아보도록 하자.

const positionX = 현재궤도요소.장반경 * (
    Math.cos(편심이각) - 현재궤도요소.이심률
  );

const positionY = 현재궤도요소.장반경 * (
    Math.sqrt(1 - (현재궤도요소.이심률 ** 2))
  ) * Math.sin(편심이각);

이를 통해 필자는 지구가 타원의 중심으로부터 X축으로 약 -76,411,956km, Y축으로는 약 130,045,428km 떨어진 곳에 위치한다는 사실을 알 수 있었다.

태양으로부터의 거리와 진근점이각 구하기

이렇게 궤도 평면 상에서 지구의 좌표를 구해볼 수 있었지만, 이 좌표는 중력 중심체인 태양이 아닌 궤도 자체의 중심에서부터의 거리를 의미한다.

하지만 필자가 알고 싶은 것은 궤도 중심으로부터의 계산한 지구의 위치가 아닌 태양으로부터의 위치이기 때문에 추가적인 계산을 진행해야한다. 이를 이해하기 위해 다시 위에서 보았던 그림을 가져와보자.

필자는 앞서 위 그림에서 나타난 편심 이각 $E$ 를 구했고, 이 값을 토대로 행성의 실제 궤도인 붉은색 궤도를 돌고 있는 $P$ 의 $x$ , $y$ 좌표를 알아낼 수 있었다. 하지만 타원 궤도를 도는 행성은 궤도의 중심인 $C$ 를 공전하는 것이 아니라 타원의 초점 중 하나에 위치한 중력 중심체를 공전한다.

중력 중심체를 공전하는 행성은 중심체와의 거리에 따라 받는 중력의 영향도 달라지고, 이로 인한 궤도 운동의 속도도 달라지기 때문에 사실 궤도 계산에서 중요한 것은 타원의 초점이 아닌 중력 중심체와의 거리와 각도이다.

즉, 이제 필자는 $C$ 가 아닌 $F$ 에서 $P$ 까지의 거리, 그리고 각도 $f$ 를 알아내야 하는 것이다. 이때 각도 $f$ 를 진짜 근점 이각이라는 의미로 진근점이각이라고 부른다.

먼저 태양의 위치에서 지구까지의 거리를 구해보자. 어차피 지구의 $x$ , $y$ 좌표를 알고 있으니 태양부터 지구의 유클리드 거리( $r$ )는 피타고라스의 원리로 간단하게 구해볼 수 있다.

r = \sqrt{(x - (a \cdot e))^2 + y^2}

이때 $a \cdot e$ 은 타원 궤도의 중심에서 태양까지의 거리를 의미하는데, 기존에 계산한 지구의 $x$ 좌표는 궤도의 중심을 기준으로 계산한 것이기 때문에 궤도 중심과 태양까지의 거리를 빼줌으로서 거리의 기준을 태양의 $x$ 좌표로 보정해준 것이다. 이 내용을 제외하면 공식 자체는 $c = \sqrt{a^2 + b^2}$ 라는 흔한 피타고라스 정리와 같은 꼴이기 때문에 자세한 설명은 생략하겠다.

const convertKMtoAU = (km: number) => km / 149_597_870;
const 거리 = Math.sqrt(Math.pow(positionX - (현재궤도요소.장반경 * 현재궤도요소.이심률), 2) + Math.pow(positionY, 2));

console.log(convertKMtoAU(거리));
// 1.0168205539250386 AU

이 공식을 바탕으로 계산을 해보면 2017년 5월 3일 22시 27분, 지구는 태양으로부터 약 1.02 AU만큼 떨어진 곳에 위치한다는 사실을 알 수 있다.

이제 태양과 지구의 거리를 구했으니, 이제는 진근점이각을 구해 지구가 궤도의 근일점을 기준으로 몇 도나 돌아간 곳에 위치한 것인지를 알아낼 차례이다.

일반적으로는 편심 이각을 사용하여 진근점이각을 계산하는 공식을 주로 사용하지만, 필자는 이미 지구의 $x$ , $y$ 좌표를 알고 있기 때문에 Math.atan2 함수를 사용하여 간단하게 진근점이각을 알아낼 수 있다.

Math.atan2 함수는 인자로 받은 y와 x의 상대적인 위치를 사용하여 특정 점이 기준점에서 형성하는 각도를 계산하는 함수이다. 이때 결과값은 -180도( $-\pi$ )에서 180도( $\pi$ ) 사이의 라디안 값으로 나타난다.

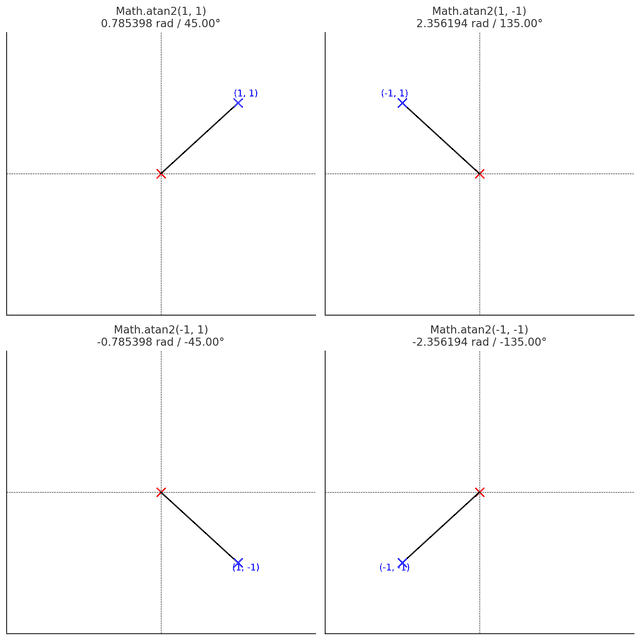atan2 함수는 원점과 양의 x축을 기준으로 각도를 잰다

참고로 이 함수는 특이하게 Math.atan2(y, x)처럼 y 좌표를 먼저 받도록 설계되어있는데, 이는 탄젠트를 표현할 때 $\tan(\theta) = \frac{y}{x}$ 와 같이 Math.tan(y / x)의 형태로 표현되기 때문이다.

이때 Math.atan2 함수가 받는 좌표들은 무조건 원점 기준으로 계산한 좌표가 아니라 임의의 원점으로부터 계산된 상대 좌표를 의미한다. 앞서 필자가 구한 지구의 $x$ , $y$ 는 태양의 위치를 기준으로 구한 좌표이므로 이 좌표들을 Math.atan2에 꽂아주기만 하면 태양을 기준으로 지구가 몇 도나 돌아간 곳에 위치한 것인지 알아낼 수 있는 것이다.

const convertRadianToDegree = (radian: number) => radian * (180 / Math.PI);
const 진근점이각 = Math.atan2(positionY, positionX - (현재궤도요소.장반경 * 현재궤도요소.이심률));

console.log('진근점이각', convertRadianToDegree(진근점이각));
// 120.4375985828049도

이렇게 필자는 2017년 5월 3일 22시 27분 기준으로 지구가 궤도 근일점으로부터 약 120도, 1.02AU만큼 떨어진 곳에 위치하고 있다는 사실을 알 수 있었다.

마치며

이 포스팅에서는 2차원 궤도 평면 상에서 행성의 위치를 구하는 것까지만 설명했지만, 결국 3차원 공간에 궤도를 배치하면서 궤도의 기울기와 근일점 편각을 반영해주면 행성은 자연스럽게 3차원 운동을 진행하게 될 것이다.

이 공식들을 사용하여 필자가 만든 시뮬레이터는 여기에서 확인해볼 수 있고, 전체 소스는 Solarsystem 프로젝트 깃허브 레파지토리에서 확인해볼 수 있다.

이상으로 행성 위치 게산하기 포스팅을 마친다.