2017-05-03프로그래밍 / 그래픽스

[JavaScript로 천체 구현하기] 케플러 6요소 알아보기

이번 포스팅에서는 태양계 시뮬레이션을 개발하면서 제일 애먹었던 천체의 궤도와 위치 계산에 대해서 알아보려고 한다. 필자는 고등학교 시절 수포자였기 대문에 필자와 같이 수포자였던 분들을 위해 최대한 간단하게 설명하는 것을 목표로 하고 있다.

먼저 궤도를 그리는 방법과 행성의 위치를 추정하는 방법에 대해서는 구글에 널리고 널렸지만, 이를 이해하기 위해서는 기본적인 천문학용어들에 대한 지식이 있어야했다. 고1 지구과학시간에 배우는 용어들이라는데 필자는 고등학교때 잠만 잤기 때문에 하나도 기억이 나지 않아서 다시 찾아봐야했다.

필자는 천체물리학과를 나온 것도 아닌 일개 개발자이므로 각각의 용어 정리에 대해서는 틀린 점이 있을 수 있다.

본격적으로 케플러 6요소를 알아보기 전에 이후 나오는 설명들의 이해를 위해 가장 기본적인 용어들부터 알아보자.

좌표와 기준면

천체는 3차원으로 무한하게 펼쳐진 공간을 운동하고 있기 때문에, 천체의 움직임을 설명하기 위해서는 반드시 좌표의 기준이 필요하다.

이때 이 기준이란 좌표의 중심점을 어디로 잡을 것이냐, 그리고 좌표 상에서 각도를 표현할 때 어디를 0도로 놓을 것이냐와 같은 것들이다.

천구와 황도

천구는 관측자를 중심으로 하여 무한대의 반지름을 가진 가상적인 구를 의미한다.

이때 관측자란 실제 인간이 아닌 관측자가 위치한 천체를 의미하는데, 인간의 경우 아직까지는 지구 외 행성에서 이런 개념을 사용할 일이 없으니 통상적으로 관측자는 지구로 한정된다. 이때 지구의 적도를 쭉 연장해서 천구에 맞닿는 그 선을 천구의 적도라고 부른다.

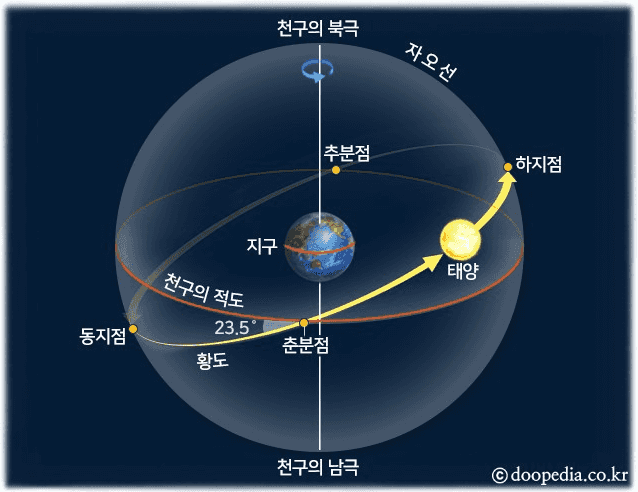
그리고 위 그림에서 황도라고 불리는 노란색 선은 지구를 중심으로 하늘을 올려다보았을 때 항성인 태양이 움직이는 선을 의미한다.

즉, 천구와 황도라는 개념은 천동설에서부터 유래된 것이라고 생각하면 된다. 관측자인 지구가 중심으로 삼아 하늘에 떠있는 천체들의 위치를 정의하는 것이다.

지구의 자전축은 23.5도 기울어져있기 때문에 천구의 적도와 황도 또한 23.5도의 기울기로 맞닿아 있다. 이러한 기울기로 인해 관측자인 지구가 태양을 바라보면 마치 태양이 지구를 빙글빙글 돌면서 지구의 남쪽으로 이동했다가 북쪽으로 이동하는 모습을 보이는데, 이때 태양이 남쪽에서 북쪽으로 올라가는 지점을 춘분점, 그리고 반대로 북쪽에서 남쪽으로 내려가는 지점을 추분점이라고 한다.

하지만 21세기를 사는 우리는 사실 태양이 지구를 도는 것이 아닌 지구가 태양을 돌고 있다는 사실을 알고 있다. 즉, 위 그림에서는 지구가 똑바로 서있고 마치 태양이 삐딱하게 지구를 돌고 있는 것처럼 표현되어있지만 실제로는 황도가 기준면이 되고 천구의 적도가 23.5도 기울어져있는 모습을 떠올릴 수 있다.

적경과 적위

천구는 결국 지구를 중심으로 하늘에 떠있는 천체들의 위치를 표현하기 위한 개념이다. 이때 천체의 위치를 표현하기 위해 적경과 적위라는 개념을 사용한다.

이는 마치 우리가 지구 상의 특정 위치를 표현하기 위해 경도와 위도를 사용한 지리 좌표계를 사용하는 것과 동일한 개념이다. 지리 좌표계의 위도는 적도를 0도라고 보고 북극과 남극을 90도로 삼아 세로 위치를 표시하고, 경도는 그리니치 천문대를 0도로 삼아 동쪽으로 180도, 서쪽으로 180도를 나누어 가로 위치를 표현한다.

이와 동일한 원리로 지구를 중심으로 하늘을 올려다보았을 때 천구 표면에 존재하는 천체의 위치도 경도와 위도 두 개의 값만 있으면 표현이 가능한 것이다.

이때 적경과 적위는 천구의 적도를 기준선으로 잡은 적도 좌표계에서의 경도와 위도를 의미한다. 이때 천체의 가로 위치를 정의하는 적경은 춘분점을 기준으로 대상 천체의 위치까지 반시계 방향으로 잰 각도를 의미하며, 천체의 세로 위치를 의미하는 적위는 천구의 적도를 기준으로 대상 천체까지의 위치를 잰 각도를 의미한다. 즉, 적도 좌표계의 기준이 되는 천구의 적도와 춘분점, 그리고 적경과 적위만 알면 천구 상에 떠있는 특정 천체의 위치를 특정할 수 있는 것이다. (물론 적도 좌표계는 대상 천체가 천구의 표면이라는 가상의 2차원 공간에 존재한다고 가정하는 것이라 대상 천체의 거리까지는 정의하지 못 한다)

재미있는 사실은 태양계 천체나 혜성과 같은 몇몇 천체를 제외한 대부분의 천체는 천구 상에서 거의 움직이지 않기 때문에 대부분의 천체는 고유한 적경과 적위를 가지므로 이 값만 알면 손쉽게 천체의 위치를 찾을 수 있다.

이때 적도 좌표계의 적경은 지리 좌표계의 경도와 다르게 시, 분과 같은 시간 단위로 표현한다. 지구는 24시간 동안 360도를 자전하기 때문에 1시간의 적경은 15도의 각도로 환산할 수 있다. 적위는 천구의 적도를 0도로 삼고 천구의 북극을 +90, 남극을 -90으로 정의하기 때문에 항상 -90부터 +90 사이의 값을 가진다.

참고로 지구의 적도가 아닌 실제 지면에 서있는 지구의 관측자를 중심으로 하고 관측자가 서있는 지면을 기준면으로 잡는 좌표계는 지평좌표계라고 한다.

궤도에 대한 용어

승교점 / 강교점

천체의 궤도는 일반적으로 기준 평면과 기울어져 있다. 이때 기준 평면은 정의에 따라 달라질 수 있는데, 태양계의 경우 황도면을 이야기한다.

앞서 살펴본 적도 좌표계에서 태양이 지구를 중심으로 회전하며 남쪽에서 북쪽으로 이동하는 지점을 춘분점, 반대로 북쪽에서 남쪽으로 내려오는 지점을 추분점이라고 한다는 설명을 했다.

이처럼 특정 중심체를 기반으로 궤도를 도는 천체가 중심체의 남쪽에서 북쪽으로 올라가는 지점을 승교점, 그리고 북쪽에서 남쪽으로 내려오는 지점을 강교점이라고 한다. 적도 좌표계에서 이야기하는 춘분점과 추분점은 지구라는 행성에 사는 우리만 사용할 수 있는 표현이지만, 승교점과 강교점은 중심체를 특정 궤도를 그리며 운동하는 모든 천체에 통용할 수 있는 용어다.

태양계의 경우 중심체가 태양이기 때문에 황도를 기준으로 잡는다.

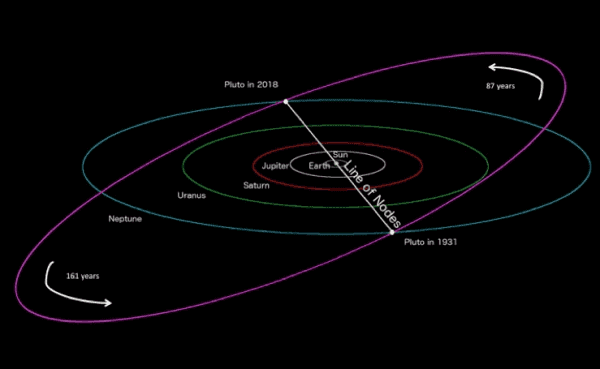명왕성의 궤도를 보면 황도를 기준으로 태양의 북쪽으로 올라가거나 남쪽으로 내려간다는게 무슨 말인지 쉽게 알 수 있다.

원일점 / 근일점

행성의 궤도는 타원이기 때문에 초점이 2개이다. 보통 이 중 하나의 초점에 항성이 위치하게 되며, 각각 원일점과 근일점은 항성에서 가장 멀리 떨어지거나 가장 가까운 한점을 의미한다. 포물선 궤도는 원일점이 무한대이므로 근일점만을 가지게 된다.

케플러 6요소

기본 용어 정리가 되었으면 이제 궤도의 모양과 크기, 방향을 결정하는 케플러 6요소를 알아보자.

케플러 6요소는 궤도의 형태와 크기를 정의하는 장반경과 이심률, 그리고 궤도면의 형태를 결정하는 기울기와 승교점 경도, 마지막으로 궤도가 놓인 방향을 결정하는 근일점 편각과 특정 시간을 기준으로 천체의 위치를 특정하기 위한 근일점 통과 시각으로 구성되어있다.

장반경

행성의 궤도는 타원이기 때문에 반지름이 아닌 장반경과 단반경으로 정의한다. 이때 장반경은 궤도 상에서 궤도 중심과 가장 거리가 먼 한 지점을 의미하며, 단반경은 궤도 상에서 궤도 중심과 가장 거리가 가까운 한 지점을 의미한다.

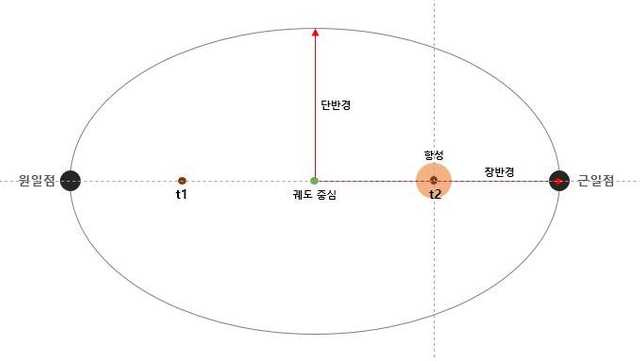
원일점, 근일점과의 차이는 측정의 기준이 되는 점이 항성이 아닌 궤도의 중심이라는 것이다. 포물선 궤도나 쌍곡선 궤도는 장반경이 무한대 이므로 단반경만을 가지게 된다.

다만 케플러 6요소에서는 장반경과 단반경 중 장반경만을 다루고 있는데, 그 이유는 궤도 에너지를 계산할 때는 궤도 자체의 모양보다는 궤도를 형성하는 천체의 평균 거리가 중요하기 때문이다. 장반경은 궤도의 전체 크기를 대표할 수 있지만 단반경은 단지 궤도의 찌그러짐 정도를 나타내는 것 뿐이므로 에너지 계산에 적합한 지표가 아니다.

그러한 이유로 일반적인 천체역햑에서는 주로 장반경을 사용하며, 케플러 방정식 또한 마찬가지이다.

이심률

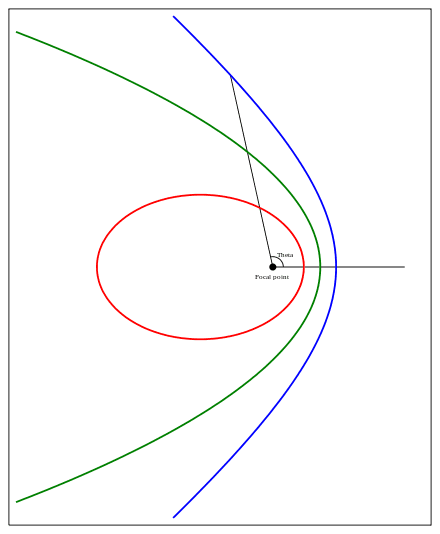
이심률은 간단히 말하면 타원이 얼마나 찌그러져있는지에 대한 값이다. 기하학적 정의에서 타원의 이심률 $e$ 는

e = \sqrt{1-\frac{b^2}{a^2}}

로 정의할 수 있으며, 이때 $a$ 는 장반경, $b$ 는 단반경이다. 그러나 케플러 궤도에서 사용하는 사용되는 이심률은 약간 공식이 달라진다.

일반적인 타원의 이심률을 구하는 공식은 중력이나 에너지와 같은 요소는 고려하지 않은 순전히 기하학적 타원의 찌그러짐 정도만을 나타내는 것이라, 타원 궤도를 형성하는 물체의 운동 에너지와 중력 간의 상호작용을 기반으로 하는 케플러 궤도의 이심률을 구하는 데에는 적합하지 않기 때문이다.

그래서 케플러 궤도의 이심률을 구할 때는 물체의 운동 에너지, 각운동량 등의 물리적 동역학을 고려하여 계산해야한다.

e = \sqrt{1+\frac{2EL^2}{m_\text{red}\alpha^2}}

이 공식의 해인 $e$ 를 궤도 이심률이라고 부른다.

여기서 $E$ 는 물체가 궤도에서 가진 전체 에너지, $L$ 은 각운동량, $m_{red}$ 는 환산 질량을 나타내며, $\alpha$ 는 역제곱 법칙 중심력의 계수이다. 역제곱 법칙이란 어떤 힘의 크기가 거리의 제곱에 반비례하는 것을 가리키는 말이다. 이 경우 어떤 힘이란 바로 중력이 된다.

하지만 필자는 이심률이 이미 주어진 데이터를 사용할 예정이므로, 사실 굳이 이렇게 까지 계산할 필요가 없다. 그냥 일반적인 이심률 공식과 계산법이 다르다는 정도만 알고 넘어가자.

케플러 궤도의 이심률은 다음 4가지의 형태로 나타난다.

원 궤도: $e = 0$
타원 궤도: $0 < e < 1$
포물선 궤도: $e = 1$
쌍곡선 궤도: $e > 1$

지구의 궤도 이심률은 현재 약 0.0167으로 거의 원형에 가깝다. 태양계 행성 중 가장 이심률이 큰 수성은 0.2056의 값을 가지고 있고, 이로 인해서 수성은 근일점에서 원일점보다 두 배 정도 태양 복사를 받는다.

원래는 0.248의 값을 가지고 있던 명왕성이 이 분야의 대빵이었지만 지금은 다들 알다시피 퇴출되었다…(아디오스…)

혜성의 경우 이심률이 상당히 다양한 편인데, 보통 주기 혜성들의 경우는 0.2에서 0.7의 값을 가지며 몇몇 궤도가 매우 찌그러진 혜성들은 거의 1에 육박하는 이심률을 가진 것도 있다.

예를 들어 혜성 중 많이 이름이 알려진 핼리 혜성의 경우 이심률이 0.967이며, 궤도가 매우 찌그러져있어서 한번 공전하는데 76년이나 걸린다. 참고로 다음 핼리 혜성의 접근 시기는 2061년이다.

기울기

항성의 황도면과 궤도 간의 기울기를 의미한다. 기울기가 90도를 초과하면 이 물체는 기울기가 0-90인 물체와 반대방향으로 공전하고 있다고 보면 된다.

승교점 경도

앞서 언급했듯이 승교점은 천체가 궤도를 돌다가 기준면을 남쪽에서 북쪽으로 통과하는 지점을 의미한다. 이때 승교점은 경도라는 각도로 표현되는데, 이는 춘분점을 기준으로 황도면에 따라 반시계 방향으로 잰 승교점까지의 각도를 나타낸다.

즉 승교점 경도를 통해 궤도 상 승교점의 위치를 3차원 좌표계에서 정의할 수 있게 된다.

근일점 편각

근일점 편각은 타원의 궤도 평면 상에서 승교점을 기준으로 근일점까지의 각도를 나타낸다. 근일점이라는 용어에서 알 수 있듯이 이 각도는 타원의 중심이 아닌 궤도의 중심, 즉 중력의 초점에서 측정한다.

이 값은 궤도 타원이 황도면과 같은 기준 평면에 대해서 얼마나 회전되어있는지를 나타내는 각도이다. 만약 근일점 편각이 0도라면 승교점과 근일점이 일치하는 것이므로 천체가 항성에 가장 근접하는 순간 승교점을 통과한다는 의미이며, 만약 근일점 편각이 90도라면 가장 근접하는 순간 기준 면에서 북쪽으로 가장 멀리 떨어진 지점에 위치하게 된다는 것을 의미한다.

근일점 통과 시각

행성이 궤도의 근일점을 통과한 시각을 의미한다.

마치며

다음 포스팅에서는 궤도를 코드로 구현해볼 예정이다. 이상으로 천문학 용어 정리 포스팅을 마친다.