2024-04-02프로그래밍

[번역] 프로그래머를 위한 카테고리 이론 - 8. 펑터의 특성

이제 펑터가 무엇인지 알았으니, 작은 펑터로부터 큰 펑터를 구축해나가는 방법에 대해서 살펴보도록 하겠다.

여기서 특히 흥미로운 부분은 카테고리 내 대상 간의 매핑에 대당하는 타입의 생성자가 확장되어 사상 간의 매핑을 포함하는 펑터가 되는 과정을 볼 수 있다는 것이다.

8.1 이항 펑터(Bifunctors)

펑터는 카테고리들의 카테고리인 Cat에서의 사상이기 때문에 사상에 대한 많은 직관들 특히 함수에 대한 직관들은 펑터에도 그대로 작용한다고 할 수 있다.

예를 들어 두 개의 인수를 가지는 함수가 있듯이, 두 개의 인수를 가지는 펑터인 이항 펑터(Bifunctors)도 존재할 수 있다. 먼저 대상에 대해서만 생각해보자면 이항 펑터는 카테고리 $C$ , 그리고 카테고리 $D$ 의 각각의 대상으로 이루어진 모든 쌍을 카테고리 $E$ 의 대상으로 매핑하는 펑터이다. 즉, 이항 헝터는 $C×D$ 로 표현되는 $C$ 와 $D$ 의 데카르트 곱에서 $E$ 로의 매핑이라고 볼 수 있는 것이다.

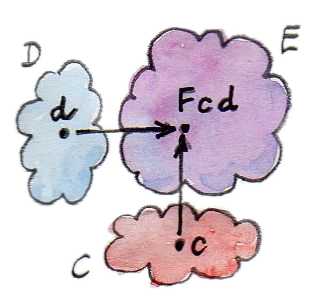
사실 여기까지는 매우 간단하게 이해할 수 있다. 그러나 펑터의 특성상 이항 펑터는 대상 뿐만 아니라 사상 또한 매핑할 수 있어야 한다. 즉, 하나는 $C$ 에서 다른 하나는 $D$ 에서 가져온 사상의 쌍을 $E$ 의 사상으로 매핑해야 한다는 것이다.

한번 더 이야기하자면, $C$ 와 $D$ 가 가진 사상의 쌍은 카테고리 $C×D$ 의 단일한 사상이다. 우리는 데카르트 곱 카테고리에서의 사상을 어떤 대상의 쌍에서 다른 대상의 쌍으로 이동하는 사상의 쌍으로 정의할 수 있다. 이러한 사상의 쌍들은 아래와 같은 방식으로 합성도 가능하다.

(f, g) ◦ (f', g') = (f ◦ f', g ◦ g')

합성은 결합법칙을 만족하며, (id, id)와 같은 항등원 또한 존재한다. 이처럼 데카르트 곱 카테고리는 카테고리의 기본적인 법칙을 모두 만족하기 때문에 실제로 하나의 카테고리가 될 수 있는 것이다.

이항 펑터에 대해서 더 쉽게 이해하려면 이 펑터가 두 인자 모두에 대한 펑터라는 점을 이해하는 것에서부터 출발해야한다. 즉, 펑터 법칙인 결합성과 항등 보존에 대한 개념을 곧바로 이항 펑터와 연결하고 확인해보려고 시도하는 것보다는, 이항 펑터가 가진 각 인자에 대해 하나씩 확인해보는 것이 더 이해하기 쉽다는 것이다.

만약 한 쌍의 카테고리로부터 세 번째 카테고리로의 매핑이 있고, 그 매핑이 각 인자에 대해 펑터적(Functorial)이라는 사실을 만족한다는 사실을 증명한다면, 해당 매핑은 자동으로 이항 펑터가 된다. 여기서 펑터적이라는 의미는 이 펑터가 사상에 대해서 제대로 된 펑터처럼 작동한다는 것을 의미한다.

Haskell에서 이항 펑터를 한번 정의해보자. 이 경우에는 세 개의 카테고리가 모두 Haskell 타입의 카테고리이기 때문에 사실상 같은 카테고리라고 볼 수 있다. 이항 펑터는 두 개의 타입 인자를 가지는 타입 생성자로 표현된다. 아래는 라이브러리 Control.Bifunctor에서 직접 가져온 Bifunctor 타입 클래스의 정의이다.

class Bifunctor f where
    bimap :: (a -> c) -> (b -> d) -> f a b -> f c d
    bimap g h = first g . second h
  	first :: (a -> c) -> f a b -> f c b
  	first g = bimap g id
  	second :: (b -> d) -> f a b -> f a d
  	second = bimap id

타입 변수 f는 이항 펑터를 나타내며, 아래 정의된 모든 타입 시그니처에서 이 타입 변수가 항상 두 개의 타입 인자에 적용되는 것을 볼 수 있다.

첫 번째 타입 시그니처는 bimap을 정의하는데, 이것은 두 함수의 매핑을 한 번에 나타낸다. 결과는 이항 펑터의 타입 생성자에 의해 생성된 타입들에서 동작하는 함수 (f a b -> f c d)이다. bimap은 first와 second를 사용하여 구현되어 있는데, 이는 이항 펑터가 각각의 인자에 대해 펑터적으로 작동한다는 사실을 정의하는 것만으로도 이항 펑터를 정의할 수 있다는 사실을 보여준다.

bimap

first와 second는 각각 첫 번째와 두 번째 인자에 대한 f의 펑터적인 성질을 증명하는 두 개의 fmap이다.

first

second

타입 클래스 정의는 bimap을 기반으로 두 개의 함수에 대한 기본 구현을 제공한다.

Bifunctor의 인스턴스를 선언할 때는 bimap을 구현하고, first와 second의 기본 값을 사용하거나, 반대로 first와 second를 모두 구현하고 bimap의 기본 값을 사용하는 선택권을 가질 수 있다. (물론 세 가지 모두를 구현할 수는 있겠지만, 그러면 이들이 위와 같은 성질을 가질 수 있도록 보장해줘야 한다.)

8.2 곱과 합 이항 펑터(Product and Coproduct Bifunctors)

이항 펑터의 예시 중 특히 중요한 것은 카테고리적 곱(Categorical Product)이다. 이는 두 대상의 곱으로, 보편적 구성(Universial Construction)에 의해 정의된다. 만약 어떤 두 대상에 대한 곱이 존재한다면, 해당 대상들에서 곱으로의 매핑은 이항 펑터적(Bifunctorial)이다. 이것은 일반적으로 참이며, 특히 Haskell에서도 마찬가지이다.

아래는 가장 간단한 곱 타입인 쌍 생성자에 대한 Bifunctor 인스턴스이다.

instance Bifunctor (,) where
    bimap f g (x, y) = (f x, g y)

여기서 bimap은 단순히 쌍의 첫 번째 구성 요소에 첫 번째 함수를 적용하고, 두 번째 구성 요소에는 두 번째 함수를 적용하고 있기 때문에, 딱히 고민할만한 부분이 없다. 이렇게 명확하고 간단한 동작이 요구사항으로 주어진다면 코드 작성 자체는 간단하다.

bimap :: (a -> c) -> (b -> d) -> (a, b) -> (c, d)

여기서 이항 펑터의 작용은 타입들의 쌍을 만드는 것이다. 예를 들면 이런 것이다.

(,) a b = (a, b)

쌍대성에 의해 이 정의가 카테고리 내의 모든 대상 쌍에 대해서 정의된다면, 합(Coproduct) 또한 이항 펑터라고 할 수 있다. Haskell에서는 Either 타입 생성자를 Bifunctor의 인스턴스인 것으로 나타낼 수 있다.

instance Bifunctor Either where
    bimap f _ (Left x) = Left (f x)
    bimap _ g (Right y) = Right (g y)

워낙 동작이 간단하고 요구사항이 명확하니 코드 작성은 어렵지 않다.

혹시 모노이드 카테고리(Monoidal Category)에 대해 이야기했던 것을 기억하는가? 모노이드 카테고리는 단위 대상과 함께 대상에 작용하는 이항 연산자인 모노이드 곱(Monoidal Product)을 정의한다.

예전에 이야기했듯이 Set(집합의 카테고리)은 데카르트 곱 연산을 이항 연산으로 사용하여 대상 간의 결합을 정의하는 모노이드 카테고리이며, 이때 단위 대상은 단일 원소 집합이다. 또한 서로소 합집합 연산에 대해서도 모노이드 카테고리라고 볼 수 있으며, 이때의 단위 대상은 공집합이 된다.

당시 필자가 언급하지 않은 것이 하나가 있다. 바로 모노이드 카테고리의 요구 사항 중 하나는 이항 연산자가 이항 펑터여야 한다는 것이다.

우리는 모노이드 곱의 연산 구조가 사상에 의해 정의된 카테고리의 구조와 호환되도록 만들어야 하며, 이것은 매우 중요한 요구 사항이다. 물론 완전한 이해를 하기에는 아직 자연성(Naturality)이라는 큰 산이 하나 남아 있기는 하지만, 그래도 모노이드 카테고리의 전체 정의에 한 발짝 더 가까워졌다.

8.3 펑터적인 대수적 데이터 자료형(Functorial Algebraic Data Types)

지금까지 펑터가 될 수 있는 몇 가지 파라미터화된 데이터 타입을 살펴봤다. 우리는 이러한 타입들에 대한 fmap을 정의할 수 있었다. 복잡한 데이터 타입은 더 간단한 데이터 타입을 기반으로 하여 구성되는데, 합과 곱의 개념을 사용하여 대수적 데이터 타입(ADT)을 생성하는 것이 바로 그 예이다.

앞선 섹션에서 우리는 이미 합과 곱이 펑터적이라는 사실을 확인했고, 펑터가 합성 가능하다는 사실도 알게 되었다. 결국 우리가 대수적 데이터 타입의 기본 구성 요소가 펑터라는 사실을 보일 수만 있다면, 파라미터화된 대수적 데이터 타입도 결국 펑터라는 사실로 이어질 수 있다는 것이다.

파라미터화된 대수적 데이터 타입이라는 것이 무엇을 의미하는걸까? 먼저 Maybe의 Nothing이나 List의 Nil처럼 펑터의 타입 파라미터에 의존하지 않는 녀석들이 있으며, 이들은 Const 펑터와 동등하다. Const 펑터는 자신이 받는 타입 파라미터를 무시한다는 사실을 기억해보자. (정확히 말하면 첫 번째 타입 파라미터는 고정이며, 두 번째 파라미터를 무시하는 것이다.)

또한 Maybe의 Just처럼 단순히 타입 파라미터 자체를 캡슐화하는 녀석들도 있다. 이들은 항등 펑터와 동등하다. 이전에 Cat에서의 항등 사상에 대한 이야기를 하면서 항등 펑터를 언급한 적이 있었지만, Haskell에서의 정의는 보여주지 않았었다. 이것이 바로 항등 펑터의 정의다.

data Identity a = Identity a

instance Functor Identity where
    fmap f (Identity x) = Identity (f x)

Identity는 항상 타입이 a인 하나의 불변 값만을 가지는 간단한 컨테이너라고 생각해볼 수 있다. 대수적 데이터 구조에서 이 개념을 제외한 나머지 것들은 모두 두 가지 원시적 요소를 합하거나 곱하여 생성된다.

이 새로운 지식을 토대로 Maybe 타입 생성자를 다시 한번 살펴보도록 하자.

data Maybe a = Nothing | Just a

이건 결국 Nothing과 Just 두 타입의 합이며, 합은 펑터적이다. 첫 번째 부분인 Nothing은 Const ()가 a에 작용하는 것이라고 볼 수 있다. (여기서 Const의 첫 번째 타입 파라미터는 유닛으로 설정한다.) 그리고 두 번째 부분인 Just는 그저 항등 펑터의 다른 이름일 뿐이다. 그럼 이제 우리는 Maybe를 동형적으로 아래와 같이 다시 정의할 수 있다.

type Maybe a = Either (Const () a) (Identity a)

결국 Maybe는 이항 펑터 Either를 사용하여 Const (), Identify라는 두 개의 펑터를 조합한 것이다. (실제로는 Const 또한 이항 펑터이지만, 여기서는 항상 부분적용된 상태로만 사용한다.)

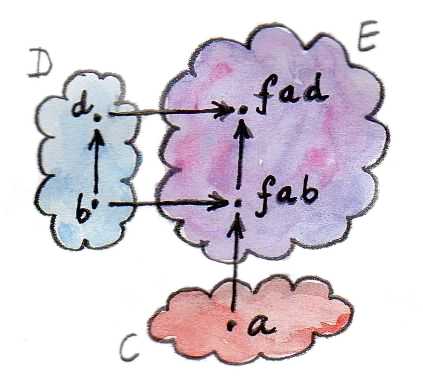
우리는 이미 펑터의 합성 또한 펑터라는 것을 알고 있으며, 이항 펑터 또한 이와 마찬가지로 동일한 원칙이 적용될 것이라는 점을 쉽게 예상해볼 수 있다. 한번 이항 펑터와 두 펑터의 합성이 사상에 어떤 식으로 작용하는지 알아보도록 하자. 먼저 두 개의 사상 중 하나를 한 펑터로 리프팅한 후, 다른 하나를 또 하나의 다른 펑터로 리프팅할 것이다. 그 다음 여기서 얻어진 두 사상의 쌍을 이항 펑터로 리프팅하는 순서로 진행하면 된다.

이 과정을 Haskell로 한번 표현해보자. 이 데이터 타입의 매개변수는 다음과 같다. 두 개의 타입을 인자로 받는 타입 생성자를 의미하는 이항 펑터 bf, 각각 하나의 타입 변수를 받는 타입 생성자인 두 개의 펑터 fu와 gu와 두 개의 일반적인 타입 a와 b이다. 이제 펑터 fu를 a에 적용하고, 펑터 gu는 b에 적용한 다음, 이 결과로 나온 타입 두 개에 이항 펑터 bf를 적용할 것이라는 것을 표현하면 된다.

newtype BiComp bf fu gu a b = BiComp (bf (fu a) (gu b))

이것은 객체 또는 타입에 대한 합성이다. Haskell에서는 타입 생성자를 타입에 적용하는 것이 마치 함수를 인수에 적용하는 것과 동일한 방식으로 이루어지며, 심지어 구문 또한 동일하다.

조금 헷갈린다면, BiComp의 매개변수로 Either, Const (), Identity, a, b가 들어온다고 생각해보자. 결과적으로 Maybe b를 얻을 수 있다.

💡 역주

왜 BiComp Either Const () Identity a b가 Maybe b인지는 의사코드로 작성해보면 단번에 알 수 있다.

type Maybe a = Either (Const () a) (Identity a)

newtype BiComp bf fu gu a b = BiComp (bf (fu a) (gu b))

BiComp Either Const () Identity a b
= BiComp (Either (Const () a) (Identity b))
= Either (Const () a) (Identity b)

새로운 타입인 Bicomp는 a와 b에 대한 이항 펑터라고 할 수 있지만, 이 정의는 매개변수인 bf가 이항 펑터이고 fu와 gu가 펑터일 경우에만 성립할 수 있다. 즉, 컴파일러가 이 매개변수들을 추론했을때, bf에 대한 bimap 정의와 fu 및 gu에 대한 fmap 정의가 있다는 사실이 보장되어야 한다는 것이다.

Haskell에서는 인스턴스 선언 시 클래스 제약 조건 집합 다음에 위치하는 이중 화살표(=>)로 이러한 전제조건을 표현해줄 수 있다.

instance (Bifunctor bf, Functor fu, Functor gu) =>
    Bifunctor (BiComp bf fu gu) where
        bimap f1 f2 (BiComp x) = BiComp ((bimap (fmap f1) (fmap f2)) x)

BiComp의 bimap 구현은 bf의 bimap과 fu, gu의 fmap을 사용하여 정의한다. 컴파일러는 BiComp가 사용될 때 이 타입들을 자동으로 추론하고 오버로드된 함수를 선택할 것이다.

위의 bimap 정의에서 x의 타입은 다음과 같다.

bf (fu a) (gu b)

이것은 꽤나 복잡한 정의처럼 보인다. 외부 bimap은 외부 bf 레이어를 통과하며, 두 개의 fmap들은 각각 fu와 gu 아래로 파고들게 된다.

만약 f1와 f2의 타입이 아래와 같은 상황이라고 가정해보자.

f1 :: a -> a'
f2 :: b -> b'

그러면 최종 결과는 bf (fu a') (gu b') 타입이 된다.

bimap (fu a -> fu a') -> (gu b -> gu b')
  	-> bf (fu a) (gu b) -> bf (fu a') (gu b')

만약 여러분이 직소 퍼즐을 좋아한다면, 이런 종류의 타입 조작에서 꽤나 큰 즐거움을 느낄 수 있을 것이다.

결론적으로 Maybe는 두 펑터적인 요소의 합으로 구성되었기 때문에, 굳이 Maybe가 펑터라는 것을 증명하지 않아도 당연히 펑터라는 사실이 성립하는 것이다.

만약 예리한 독자들은 대수적 데이터 타입에 대한 펑터 인스턴스의 유도가 이렇게 논리적으로 명확하게 정의될 수 있다면, 그냥 컴파일러에서 자동화해서 처리할 수는 없냐고 질문할 수도 있다.

물론 가능하다. 이는 Haskell의 확장기능(Extensions)를 사용하면 되는데, 특정 확장기능을 사용하려면 소스 파일의 맨 위에 아래와 같은 라인을 추가하면 된다.

{-# LANGUAGE DeriveFunctor #-}

그 이후 데이터 구조에 deriving Functor를 추가하자.

data Maybe a = Nothing | Just a deriving Functor

이처럼 DeriveFunctor 확장 기능을 사용하면 특정 데이터 구조에 대한 fmap이 자동으로 구현되도록 할 수 있다.

이런 기능이 제공될 수 있는 이유는 대수적 데이터 구조의 규칙성으로 인해 Functor뿐 아니라 앞서 언급했던 Eq와 같은 여러 다른 타입 클래스 인스턴스를 논리적으로 유도하는 것이 가능하기 때문이다.

이와 더불어 컴퍼일러에게 사용자 정의 타입 클래스의 인스턴스를 유도하는 것도 가능하지만 이것은 조금 더 고급 기능이다. 하지만 결국 사용자 정의 타입 클래스라고 해도 기본적인 구성 요소, 그리고 합과 곱의 동작을 제공하는 것 뿐이므로 근본적인 원리는 동일하다.

8.4 C++에서의 펑터(Functors in C++)

만약 여러분이 C++ 프로그래머라면 펑터를 처음부터 끝까지 오롯이 혼자서 구현해야할 것이다. 그러나 이를 위해서는 C++이 가진 대수적 데이터 구조의 몇 가지 타입을 이해할 수 있어야하며, 이런 데이터 구조를 일반적인 템플릿으로 구현하고 이 구조에 대한 fmap 또한 직접 구현할 수 있어야한다.

먼저 Haskell에서 재귀적인 합 타입으로 정의된 트리 데이터 구조를 한번 살펴보자.

data Tree a = Leaf a | Node (Tree a) (Tree a)
    deriving Functor

앞서 언급한 대로, C++에서 합 타입을 구현하는 방법 중 하나는 바로 클래스 계층 구조를 이용하는 것이다. 객체지향 언어에서는 기본 클래스 Functor의 가상 함수(Virtual functions)로 fmap을 구현한 뒤 모든 하위 클래스에서 이를 재정의하는 방향이 자연스러울 것이다.

하지만 아쉽게도 이런 방법을 사용하는 것은 불가능하다. 왜냐하면 결국 fmap은 템플릿이며, 이는 this 포인터로 전달되는 객체의 타입 뿐 아니라 적용된 함수의 반환 타입이 매개변수화되어야 한다는 것을 의미한다. 하지만 C++에서는 가상 함수를 템플릿화 할 수 없다. 대신 우리는 dynamic_cast를 사용하여 패턴 매칭을 대체하고 fmap을 일반적인 자유 함수로 구현할 것이다.

기본 클래스는 동적 캐스팅을 지원하기 위해 최소 하나의 가상 함수를 정의해야하며, 이 경우 우리는 소멸자(Destructor)를 가상 함수로 정의할 것이다.

template<class T>
struct Tree {
    virtual ~Tree() {};
};

숨겨진 Identity 펑터인 Leaf를 정의하자.

template<class T>
struct Leaf : public Tree<T> {
    T _label;
    Leaf(T l) : _label(l) {}
};

Node는 곱 타입으로 정의할 것이다.

template<class T>
struct Node : public Tree<T> {
    Tree<T> * _left;
    Tree<T> * _right;
    Node(Tree<T> * l, Tree<T> * r) : _left(l), _right(r) {}
};

fmap을 구현할 때는 Tree의 타입에 따른 동적 디스패치를 활용할 것이다. Leaf의 경우에는 Identify 버전의 fmap을 적용하고, Node의 경우에는 두 개의 Tree 펑터의 복사본과 결합된 이항 펑터처럼 처리할 것이다. 물론 C++ 프로그래머들은 이런 사고 방식과 용어로 코드를 분석하는 것에 익숙하지 않을 수 있지만, 이 모든 과정이 결국 카테고리론적 사고를 연습하는 것이다.

template<class A, class B>
Tree<B> * fmap(std::function<B(A)> f, Tree<A> * t) {
    Leaf<A> * pl = dynamic_cast <Leaf<A>*>(t);
    if (pl)
        return new Leaf<B>(f (pl->_label));
    Node<A> * pn = dynamic_cast<Node<A>*>(t);
    if (pn)
        return new Node<B>(fmap<A>(f, pn->_left), fmap<A>(f, pn->_right));
    return nullptr;
}

여기서는 간결함을 위해 메모리나 리소스 관리 문제를 무시하고 있지만, 실제 코드에서는 정책에 따라 unique나 shared 같은 스마트 포인트를 사용할 것이다.

이렇게 C++로 작성한 Tree의 fmap을 Haskell에서 작성한 버전으로 바꿔보자면 다음과 같다.

instance Functor Tree where
    fmap f (Leaf a) = Leaf (f a)
    fmap f (Node t t') = Node (fmap f t) (fmap f t')

그리고 이 역시 DeriveFunctor 확장 기능을 사용하면 컴파일러에 의해 자동으로 구현될 수 있다.

8.5 Writer 펑터

이전에 설명했던 크라이슬리 카테고리(Kleisli Category) 섹션에서 Writer 펑터에 대해서 다시 설명하겠다고 했던 것을 기억하는가? 해당 카테고리에서의 사상들은 꾸며진(embellished) 함수로 표현되어 Writer 데이터 구조를 반환했었다.

type Writer a = (a, String)

필자는 이렇게 꾸며진 기능이 어떤 방식으로든 엔도 펑터와 관련이 있다고 말했다. 그리고 실제로 Writer 타입 생성자는 a에 대해 펑터적이다. 심지어 이를 위해 fmap을 구현할 필요도 없다. 왜냐하면 반환된 타입은 단순한 곱 타입이기 떄문이다.

일반적으로 크라이슬리 카테고리와 펑터 간의 관계는 다음과 같다. 크라이슬리 카테고리는 카테고리이기 때문에 합성과 항등성을 정의해야한다. 그리고 합성은 fish(>=>) 연산자에 의해 제공된다.

(>=>) :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
m1 >=> m2 = \x ->
    let (y, s1) = m1 x
        (z, s2) = m2 y
    in (z, s1 ++ s2)

그리고 항등 사상은 return이라고 불리는 함수를 통해 제공했다.

return :: a -> Writer a return x = (x, "")

이제 이 두 함수들의 타입을 오랜 시간 들여다 보다보면, fmap으로 사용할 수 있는 올바른 타입의 함수를 생성하는 방법을 찾을 수 있다.

fmap f = id >=> (\x -> return (f x))

위 예시에서 fish 연산자는 우리에게 익숙한 id, 그리고 인수에 f를 적용한 결과에 다시 return을 적용한 람다, 두 함수를 합성한다.

아마 여기서 가장 이해하기 어려운 부분은 id의 사용법일 것이다. fish 연산자의 인수는 Int, Bool과 같은 일반 타입을 가져와서 꾸며진(embellished) 타입을 반환하는 함수여야 한다고 생각할 수 있겠지만 사실은 아니다. 아무도 a -> Writer b에서의 a가 일반 타입이어야 한다고 한 적은 없다. 이것은 그저 타입 변수일뿐이므로 어떤 것이든 될 수 있으며, 심지어 Writer b와 같이 이미 꾸며진 타입이 될 수도 있다.

그래서 id는 Writer a를 받아서 그대로 Writer a를 반환할 것이다. fish 연산자는 a의 값을 꺼내어 람다의 x 인자로 전달할 것이다. 이후 f는 그것을 b로 변환하고, return은 이 결과를 꾸며 최종적으로 Writer b로 만들 것이다. 이 모든 것을 조합한다면 우리는 Writer a를 가져와 Writer b를 반환하는 함수를 얻게된다. 즉, Writer의 fmap이 해야하는 것과 정확히 같은 일을 하는 것이다.

이 정의에서 Writer는 다른 임의의 타입 생성자로 변경될 수 있기 때문에 이 인자는 매우 일반적이라고 할 수 있다. 뭐가 되었던 fish 연산자와 return을 지원한다면 이를 활용하여 fmap을 정의할 수 있다는 것이다. 따라서 크라이슬리 카테고리에서의 장식(embellishment)은 항상 펑터라고 할 수 있다.

사실 우리가 방금 정의했던 fmap과 deriving Functor 확장 기능을 통해 컴파일러가 생성해주는 fmap은 동일하다. 이는 Haskell이 다형성 함수를 구현하는 방식 때문인데, 이를 매개변수 다형성(Parametric polymorphism)이라고 하며, 공짜 정리(Theorems for free)라고 불리는 정리의 원천이다.

💡 역주

매개변수 다형성(Parametric polymorphism)은 함수나 데이터 유형이 여러 타입에 대해 동작할 수 있도록 하는 기능이며, 타입스크립트의 Generic Type도 매개변수 다형성의 구현 중 하나이다.

공짜 정리(Theorems for free)는 어떤 하나의 정리를 통해 다른 정리가 추가적인 증명없이도 자동으로 성립하는 것을 의미하므로, 매개변수 다형성 또한 공짜 정리의 한 측면이라고 볼 수 있는 것이다. 타입스크립트로 예를 들자면 다음과 같다.
function nonEmptyArray<T>(arr: T[]) {
	return arr.length > 0;
}
nonEmptyArray 함수는 인자가 number[] 타입이든 string[] 타입이든 상관없이 일관된 동작을 제공한다. 즉, 다형적인 동작이 제대로 정의되었다면, number[] 타입에 대해 제대로 작동한다는 사실이 증명됨과 함께 string[] 타입에 대한 동작이 제대로 작동한다는 보장도 함께 공짜로 성립되는 것이다.

이러한 정리가 의미하는 것 중 하나는 특정 타입 생성자에 대한 fmap이 존재하고 이 함수가 항등성을 보존하고 있다면, 그 구현 방법은 유일해야 한다는 것이다.

8.6 공변적 펑터와 반공변적 펑터(Covariant and Contravariant Functors)

Writer 펑터에 대해서 살펴보았으니, Reader 펑터도 다시 한번 살펴보자. 다시 한번 이야기하지만 Reader 펑터는 부분적용된 함수 화살표 타입 생성자를 기반으로 한다.

(->) r

이 정의를 타입 동의어를 사용하여 다시 작성해보면 다음과 같다.

type Reader r a = r -> a

그리고 Reader의 Functor 인스턴스는 아래와 같이 정의된다.

instance Functor (Reader r) where
    fmap f g = f . g

쌍 타입 생성자나 Either 타입 생성자와 마찬가지로 함수 타입 생성자 또한 두 개의 타입 인자를 받는다. 기억을 되짚어보면 쌍과 Either는 자신들이 받는 각각의 인자에 대해 펑터적이었고, 이를 이항 펑터(bifunctor)라고 한다고 했다. 그렇다면 함수 생성자도 두 개의 타입 인자를 받고 있으니 이들과 동일하게 이항 펑터일까?

백문이불여일견이니 직접 확인해보자. 우선 첫 번째 인자에 대해 펑터적인지 확인해보겠다. 우선 타입 동의어에서부터 시작해볼 것이다. 아래 정의는 Reader에서 단지 인수의 순서만 뒤바뀐 형태이다.

type Op r a = a -> r

여기서 반환 타입인 r을 고정하고 인수 타입인 a에 변형을 가할 것이다. 그리고 a를 변형하는 fmap을 구현하기 위한 타입 시그니처는 다음과 같다.

fmap :: (a -> b) -> (a -> r) -> (b -> r)

인수로 a를 받고 각각 b와 r을 반환하는 두 개의 함수만 있는 경우, 이들을 사용하여 b를 받아 r을 반환하는 함수를 만들 수 있는 방법은 존재하지 않는다.

하지만 첫 번째 함수를 반대로 뒤집을 수 있다면 상황은 달라진다. 즉, 첫 번째 함수가 b를 받아 a를 반환하는 함수가 되도록 만들어주면 되는 것이다. 우리는 임의의 함수를 막 뒤집을 수는 없지만, 반대 카테고리로 이동해볼 수는 있다.

💡 역주

필자가 Reader에 대한 설명을 하다가 갑자기 반대 카테고리에 대한 이야기를 하고 있어서 설명의 흐름이 어색하다. 결과적으로 말하자면 Reader r a는 두 인자를 받아 r을 a로 변형하는 매핑을 의미하기 때문에 이항 펑터가 아니다.

앞서 보았던 쌍이나 Either의 경우 자신들이 받는 인수의 순서를 변경하더라도 연산의 결과는 동일하게 보장된다.
instance Bifunctor (,) where
    bimap f g (x, y) = (f x, g y)
-- 패턴 매칭을 통해 연산을 적용하기 때문에
-- 인자의 순서가 g f (x, y)가 되어도 f는 x에, g는 y에 적용된다.
그러나 Reader 펑터의 fmap은 함수의 합성이기 때문에 첫 번째 인자의 결과가 두 번째 인자에 의존하게 된다.
instance Functor (Reader r) where
	  fmap f g = f . g
-- 만약 합성의 순서가 g . f가 된다면 연산 결과가 달라지거나
-- 혹은 합성 자체가 불가능한 상황이 발생할 수도 있다.
필자는 이러한 Reader 펑터의 특성을 보이기 위해, 인수의 순서를 반대로 뒤집은 Op라는 타입을 예로 들어 설명하고 있는 것이다.

반대 카테고리가 기억나지 않을 수 있으니 간단하게 복습해보자. 모든 카테고리 $C$ 에 대한 반대 카테고리 $C^{op}$ 는 $C$ 와 같은 대상들을 가지고 있지만 모든 화살표(사상)의 방향이 반대로 뒤집어진 카테고리이다.

그럼 이제 $C^{op}$ 와 다른 임의의 카테고리 $D$ 사이를 이동하는 펑터를 떠올려보자.

F::C^{op} → D

이런 펑터는 $C^{op}$ 의 어떤 사상 $f^{op} :: a → b$ 를 $D$ 의 사상 $F f^{op} :: F a → F b$ 로 매핑한다. 그러나 사상 $f^{op}$ 는 원래 카테고리 $C$ 에서의 어떤 사상 $f :: b → a$ 에 해당한다. $a$ 와 $b$ 가 서로 반전되어있음에 주목하자.

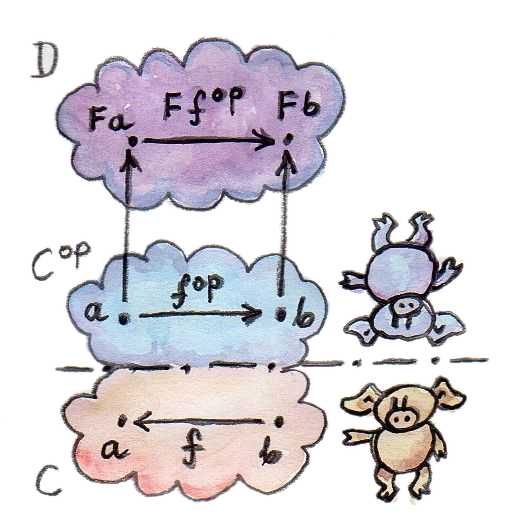
이렇게 반대 카테고리 $C^{op}$ 에서 카테고리 $D$ 로 나아가는 펑터 $F$ 를 정의했다. 그렇다면 이제 $F$ 를 사용하여 카테고리 $C$ 에서 카테고리 $D$ 로 바로 나아가는 $G$ 라는 매핑도 생각해볼 수 있다. 즉, $G$ 는 $C$ 에서 $D$ 로의 매핑이다. 하지만 사실 $G$ 는 펑터가 아니다. $F$ 와 마찬가지로 대상들을 동일하게 매핑하지만, 사상을 매핑할 때는 반대로 뒤집어서 매핑하기 때문이다.

$G$ 는 $C$ 의 사상 $f :: b → a$ 를 반대 사상인 $f^{op} :: a → b$ 로 매핑한 다음, 이를 펑터 $F$ 에 적용하여 $F f^{op} :: F a→F b$ 를 얻어야 한다.

주어진 조건에 따라 $Fa$ 는 $Ga$ 와 동일하고, $Fb$ 가 $Gb$ 와 동일하다고 가정할 때, 전체적인 흐름은 아래와 같이 나타내볼 수 있다.

G f :: (b → a) → (G a → G b)

이렇게 사상의 방향을 반전하는 카테고리 간의 매핑을 반공변적 펑터(Contravariant Functor)라고 한다. 반공변적 펑터는 반대 카테고리에서의 일반적인 펑터일 뿐이다. 그리고 우리가 지금까지 공부해왔던 일반적인 펑터는 공변적 펑터(Covariant Functor)라고 한다.

아래는 Haskell에서 반공변적인 (엔도)펑터를 정의하는 타입 클래스이다.

class Contravariant f where
  	contramap :: (b -> a) -> (f a -> f b)

즉, 아까 정의했던 타입 생성자 Op의 인스턴스는 아래와 같이 정의될 수 있다.

instance Contravariant (Op r) where
  	-- (b -> a) -> Op r a -> Op r b
  	contramap f g = g . f

함수 f가 Op의 내용인 함수 g의 앞에 자신을 삽입한다는 것에 주목하자. (함수 합성의 연산 순서는 오른쪽에서 왼쪽이다.)

여기서 Op의 contramap의 정의는 단지 인자를 뒤집은 함수 합성 연산자일 뿐이라는 것을 알 수 있으며, 이 사실을 알았다면 이제 더 간결하게 만들어 볼 수도 있다.

여기 인자를 뒤집는데 사용되는 특수한 함수인 flip이 있다.

flip :: (a -> b -> c) -> (b -> a -> c)
flip f y x = f x y

그러면 이제 contramap의 정의를 이렇게 간단하게 바꿔볼 수 있다.

contramap = flip (.)

8.7 프로펑터(Profunctors)

우리는 함수 화살표 연산자가 첫 번째 인자에서 반공변 변형이 되고, 두 번째 인자에서 공변 변형이 되는 상황을 보았다. 이런 개념에 대한 명칭도 있을까?

만약 대상 카테고리가 Set이라면 이 개념을 프로펑터(Profunctor)라고 부른다. 반공변적 펑터는 반대 카테고리에서의 공변적 펑터와 동일하기 때문에, 프로펑터는 아래와 같이 정의된다.

C^{op} × D → Set

일단 Haskell 타입을 집합이라고 가정해보면, 우리는 첫 번째 인자에 대해 반공변적 펑터적이고 두 번째 인자에 대해서는 펑터적인 두 개의 인자를 받는 타입 생성자 p에 Profuctor라는 이름을 부여할 수 있다. 아래는 Data.Profuctor 라이브러리에서 가져온 타입 클래스의 모습이다.

class Profunctor p where
  	dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
  	dimap f g = lmap f . rmap g
  	lmap :: (a -> b) -> p b c -> p a c
  	lmap f = dimap f id
  	rmap :: (b -> c) -> p a b -> p a c
    rmap = dimap id

세 함수 모두 기본 구현이 제공된다. Bifunctor와 마찬가지로 Profuctor의 인스턴스를 선언할 때는 dimap을 구현하고 lmap과 rmap에 대한 기본값을 사용하거나, 혹은 lmap과 rmap을 모두 구현하고 dimap에 대한 기본값을 사용할 수 있는 선택권이 있다.

여기까지 왔으면 이제 함수 화살표 연산자가 Profuctor의 인스턴스라는 것을 단언할 수 있다.

instance Profunctor (->) where
    dimap ab cd bc = cd . bc . ab
    lmap = flip (.)
    rmap = (.)

프로펑터는 Haskell 렌즈 라이브러리에서 응용되고 있으며, 추후 ends와 coends에 대해 이야기할 때 다시 한번 자세히 설명할 것이다.