2024-02-27프로그래밍

[번역] 프로그래머를 위한 카테고리 이론 - 5. 곱과 합

고대 그리스의 시인 에우리피데스가 “사귀는 친구를 보면 그 사람을 알 수 있다.”라고 말했듯이, 우리의 존재는 우리가 가진 관계를 통해 정의된다. 카테고리 이론에서는 이 개념이 더더욱 중요하다. 만약 우리가 어떤 카테고리 내에 존재하는 특정 대상에 대해 명확하게 설명하기 위해서는 그 대상과 다른 대상들과의 관계까지도 함께 보아야 하기 때문이다. 그리고 이러한 관계는 사상(Morphism)에 의해 정의된다. (물론 여기서 관계라 함은 항등 사상으로 표현되는 자기 자신과의 관계 또한 포함된다.)

카테고리 이론에는 “보편적 구성(Universal Construction)”이라고 불리는 방법이 존재한다. 이 구조는 각 대상들이 가지고 있는 관계를 통해 대상 자체를 정의하는 방법 중 하나이다. 이 방법은 먼저 특정 대상, 그리고 그 대상과 다른 대상 간의 관계를 나타내는 사상으로 구성된 특별한 패턴을 선택하고, 이 패턴이 카테고리 안에서 어떤 방식으로 나타나는지를 찾아내는 방식으로 진행된다. 만약 이 패턴이 일반적이고 카테고리의 크기가 충분히 크다면 이 패턴과 매칭되는 결과 또한 매우 많을 것이다. 결국 이 구성 방법의 핵심은 이렇게 찾아낸 무수한 결과들을 특정한 기준으로 평가하고 랭킹을 매겨 가장 적합한 결과를 찾아내는 것이다.

이 과정은 마치 웹에서 검색을 하는 방식과 유사하다. 검색 쿼리는 일종의 패턴이다. 만약 이 쿼리가 매우 일반적인 쿼리라면 무수히 많은 쿼리 결과가 노출될 것이다. 이 결과 중 일부는 우리가 질의한 쿼리와 관련이 있을 수도 있지만 어떤 것들은 관련이 없을 수도 있다. 결국 우리는 관련없는 결과들을 제외하기 위해 쿼리를 더 세밀하게 다듬어가며 검색의 정확도를 높혀나간다. 최종적으로 검색 엔진은 이렇게 질의된 검색 결과들에게 랭킹을 매겨 결과를 순위 별로 나열하고, 사용자가 가장 관심을 가질만한 결과를 검색 결과 리스트의 최상단에 위치시킬 것이다.

5.1 초기 대상(Initial Object)

카테고리 내에서 가장 단순한 형태는 단일 대상 그 자체이다. 아마 이렇게 단순한 형태의 패턴을 가진 무언가를 카테고리 내에서 찾아본다면, 당연히 패턴에 매칭되는 결과는 매우 많을 것이다.

이처럼 일반적인 패턴을 사용하면 너무 많은 매칭 결과가 나오기 때문에, 우리는 이 결과들에 랭킹을 매길 수 있는 기준을 정하고 이 랭킹에서 비롯된 계층구조 내에서 가장 최상위에 있는 대상을 찾아야 한다. 앞서 말했듯이 이러한 대상을 정의하기 위해 우리가 사용해볼 수 있는 유일한 수단은 바로 사상이다.

사상을 대상에서 다른 대상으로 향하는 일종의 화살표라고 생각해보자. 이 경우 카테고리의 한쪽 끝에서 다른쪽 끝으로 향하는 전반적인 화살표의 흐름이 존재할 수 있고, 만약 카테고리가 부분순서(Partial Order)와 같이 정렬되었다면 이 가정은 반드시 참이다. 그렇다면 어떠한 대상 a에서 다른 대상 b로 향하는 화살표(사상)가 존재하는 경우, “a가 b보다 더 초기적(Initial)이다”라고 정의하여 대상의 선행성이라는 개념을 일반화해볼 수 있다.

이제 우리는 초기 대상이라는 개념을 “다른 모든 대상들로 향하는 화살표를 가진 대상”이라고 정의할 것이다. 물론 카테고리 내에 이런 대상이 반드시 존재하리란 보장은 없겠지만, 사실 이 문제보다는 오히려 이런 성질을 가진 대상이 너무 많을 수 있다는 것이 문제가 될 것이다. 다시 말해 쿼리의 검출율(Recall)은 높지만 정밀도(Precision)가 부족하다는 뜻이다.

이 문제의 해결책에 대한 힌트는 정렬되어있는 카테고리(Ordered Categories)에서 얻을 수 있다. 대상 간의 순서가 명확하게 정의된 카테고리에서는 두 대상 간 최대 하나의 화살표만 허용되기 때문이다. 이러한 카테고리에서 어떤 대상이 다른 대상보다 작거나 같을 수 있는 방법은 하나 뿐이다. 이러한 사실을 토대로 우리는 초기 대상에 대해 다음과 같은 정의를 내려볼 수 있다.

👉 “초기 대상”은 해당 카테고리 내에서 다른 대상으로 향하는 단 하나의 사상을 가진 유일한 대상이다.

그러나 비록 이렇게 초기 대상에 대해 정의를 했고 실제로 초기 대상이 카테고리 안에 존재하는 것이 확인되었다고 해서 초기 대상이 카테고리 내에 유일하게 존재한다는 사실을 보장하는 것은 또 다른 이야기이다. 초기 대상의 유일성을 보장하기 위해 우리가 사용해볼 수 있는 유용한 아이디어는 바로 동형성(Isomorphism)이다. 동형성은 카테고리 이론에서 굉장히 중요한 부분을 차지하기 때문에 조만간 이에 대해서도 다룰테지만, 일단 지금은 동형성에 따라 초기 대상의 유일성을 보장할 수 있다는 점만 언급하고 넘어가도록 하겠다.

간단한 예시를 한 번 보자. Poset이라고도 부르는 부분순서집합(Paritally Ordered Set)에서의 초기 대상은 이 집합에서 가장 작은 요소이다. 물론 이 개념이 모든 Poset에 적용되는 것은 아니고, 모든 정수(양수, 0, 음수)의 집합에 “작거나 같음” 관계를 적용한 특정 Poset같은 경우는 초기 대상이 존재하지 않는다.

💡 역주

초기 대상은 카테고리 내의 다른 모든 대상으로 향하는 사상을 가져야 한다. 그러나 “작거나 같음”이라는 사상을 가진 정수 집합은 무한 집합이기 때문에 “모든 정수에 대해 작거나 같기만 하는 관계를 가진 대상”이 존재할 수 없으므로 초기 대상이 존재하지 않는 것이다.

반면 집합과 함수로 이루어진 카테고리에서 초기 대상은 공집합으로 정의할 수 있으며, 공집합은 Haskell에서의 Void 타입에 해당한다. 지난 챕터에서 우리가 Void 타입에서 임의의 다른 타입 a로 나아가는 absurd 함수를 정의했던 것을 기억하는가?

absurd :: Void -> a

바로 이러한 종류의 사상들이 타입으로 이루어진 카테고리에서 Void를 초기 대상으로 만들어주는 녀석들이다.

5.2 종결 대상(Terminal Object)

자, 단일 대상에 대한 패턴 이야기를 계속 해보자. 이번에는 대상에 대한 랭킹을 매기는 방식을 변경해볼 것이다. 우리는 어떠한 대상 b에서 대상 a로 향하는 사상이 있는 경우 ”a가 b보다 더 종결적(Terminal)이다”라고 이야기할 수 있다. 앞서 보았던 초기 대상과는 방향이 정반대라는 점에 주목하자. 우리는 카테고리 안에서 다른 대상들보다 더 많이 종결적인 대상을 찾아볼 것이다. 그리고 다시 한번 말하지만 이 검색 결과는 고유성을 가져야 한다.

👉 종결 대상은 카테고리 내의 모든 객체로부터 오는 유일한 화살표를 가진 유일한 대상이다.

초기 대상과 마찬가지로 종결 대상 또한 동형성에 따라 카테고리 내에서 유일하게 존재한다고 이야기할 수 있다. 이에 대해서는 조만간 다시 설명하겠다.

먼저 몇 가지 예제를 한번 살펴보도록 하겠다. 만약 Poset 내부에 종결 대상이 존재한다면 이는 아마 가장 큰 요소일 것이다. 집합의 카테고리에서의 종결 대상은 단일원소집합이다. 이미 우리는 단일원소집합에 대해서도 한번 이야기를 했었는데, 단일원소집합은 C++의 void 타입, Haskell에서는 ()로 표현되는 Unit 타입에 해당한다.

이것은 단 하나의 값만을 가진 타입으로, C++에서는 이러한 사실을 암묵적으로 표현하지만 Haskell에서는 () 라는 빈 괄호의 형태를 통해 명시적으로 표현하고 있다. 또한 이전 챕터에서 어떤 임의의 타입에서 Unit 타입으로 향하는 순수 함수는 단 하나만 존재할 수 있다는 사실 또한 언급했었다.

unit :: a -> ()
unit _ = ()

이렇게 종결 대상에 대한 모든 조건이 만족되었다.

종결 대상에 대한 예시에서 유일성에 대한 조건이 중요한 이유는 결국 공집합을 제외한 다른 모든 집합들도 각각의 집합으로부터 오는 사상을 가질 수 있기 때문이다. 예를 들면 모든 타입을 받을 수 있고 Boolean 타입의 값을 반환하는 사상인 Predicate 함수가 있다.

yes :: a -> Bool
yes _ = True

그러나 Bool 타입은 종결 대상이 아니다. 다른 타입에서 Bool 타입으로 향하는 함수는 yes _ = True 외에도 하나가 더 있기 때문에 유일한 사상이라고 말할 수 없기 때문이다.

no :: a -> Bool
no _ = False

즉, 우리는 종결 대상은 유일해야한다는 조건을 통해 종결 대상의 정의를 단 하나의 타입으로 좁힐 수 있는 정밀도를 만들어낼 수 있다.

5.3 쌍대성(Duality)

여기까지 오면 여러분은 아마 초기 대상과 종결 대상을 정의하는 방식 간에 대칭성이 존재한다는 사실을 눈치챘을 것이다. 이 두 정의 사이의 유일한 차이점은 그저 사상의 방향 뿐이었다. 여기서 한발짝 더 나아가보자면 이제 우리는 어떤 카테고리 $C$ 가 가진 모든 사상의 방향을 반대로 뒤집어서 반대 카테고리 $C^{op}$ 를 정의할 수도 있을 것이다.

반대 카테고리는 그저 특정 카테고리의 사상의 방향을 반대로 뒤집은 것 뿐이니 당연히 사상의 합성 규칙이나 다른 요구사항도 만족한다. 만약 원래 카테고리에서 사상 f::a->b와 g::b->c가 사상 h::a->c로 합성되었다면, 반대 카테고리의 뒤집힌 사상인 f^op::b->a와 g^op::c->b 또한 h^op::c->a로 합성된다는 것이다. 그리고 각 대상에 대한 항등사상을 반대로 뒤집는 것은 의미가 없으므로, 항등사상은 그대로 유지된다.

쌍대성(Duality)이라는 개념은 수학자들이 카테고리 이론을 사용할 때의 생산성을 두 배로 높혀주기 때문에 꽤 중요한 속성으로 취급된다. 우리가 구성한 모든 것들에는 그와 대응하는 것들이 존재하며, 증명하는 모든 정리들에 대응하는 정리들 또한 자동으로 따라오기 때문이다.

반대 카테고리의 구성 요소들은 곱(product)와 쌍대곱(coproduct), 모나드(monad)와 쌍대모나드(comonad), 콘(cone)과 쌍대콘(cocone), 극한(limit)과 쌍대극한(colimit)과 같이 “co 또는 쌍대”라는 접두사가 붙어있다. 그러나 cocomonad와 같은 개념은 존재하지 않는다. 왜냐하면 화살표를 두 번 뒤집으면 다시 원래 상태로 돌아오기 때문이다.

즉, 위의 정의에 따라 반대 카테고리에서의 초기 대상은 종결 대상이다.

5.4 동형성(Isomorphisms)

우리는 프로그래머로서 같다는 개념, 즉 동등성(Equality)을 정의한다는 것이 쉽지 않다는 것을 이미 잘 알고 있다. 두 개의 대상이 같다는 것은 무엇을 의미하는 걸까? 메모리에서 동일한 위치를 차지하는 것을 의미할까? 이 대상이 집합이라면 원소들이 전부 동일하면 같다고 봐야할까? 혹은 하나는 실수부와 허수부로 표현되고, 다른 하나는 크기와 각도로 표현되는 복소수라면 이 두 복소수는 같다고 봐야할까?

아마 여러분은 수학자들이 이미 동등성에 대한 의미를 찾아냈을 것이라고 생각하겠지만, 사실 수학자들도 아직 동등성이 무엇인가에 대한 명확한 정의를 내리지 못 했다. 동등성에 대한 정의에는 명제 동등성, 의미 동등성, 확장 동등성, 호모토피 유형 이론에서의 경로로 정의되는 동등성 등 여러가지 방법이 제시된다. 그리고 동등성보다 더 약한 개념인 동형성, 그리고 동형성보다도 더 약한 개념인 등가성이라는 개념도 있다.

우선 동형에 대해 직관적으로 이해해보자면 동형이라는 의미는 동일한 형태를 가지고 있다는 말이니 동형인 대상들은 서로 비슷하게 보일 것이다. 비슷하게 보인다는 것은 어떤 한 대상의 각 부분들이 다른 대상의 어떠한 부분과 일대일로 대응된다는 것을 의미한다. 즉, 상대적인 상황에 따라 조금씩 달라질 수는 있지만 대체로 동형인 두 대상은 서로 완벽한 복사본처럼 보일 수 있다는 것이다.

수학적으로 이야기해보자면 어떤 대상 a에서 대상 b로의 매핑이 존재하고 대상 b에서 대상 a로 향하는 매핑이 존재하며, 이 두 매핑이 서로의 역함수라는 것을 의미한다. 또한 우리는 이미 카테고리 이론에서 이러한 매핑을 사상이라고 한다는 것을 잘 알고 있다. 정리해보자면 두 대상이 동형이라는 의미는 두 대상이 서로에게 향하는 사상을 가지고 있고, 이 사상들이 서로의 반대 개념인 역사상(Inverse Morphism)이 되어야 한다는 것이다.

이러한 역사상에 대한 개념은 합성과 항등이라는 개념을 통해 이해하는 것이 쉽다. 사상 g가 사상 f의 역사상이라면, 이 두 사상의 합성사상은 항등사상이 되어야 한다. 이러한 관계를 나타낼 수 있는 식은 총 두 가지가 있다.

f . g = id
g . f = id

앞서 필자가 초기 대상이나 종결 대상이 동형성을 기준으로 했을때 카테고리 내에 유일하게 존재한다고 말한 것은 어떤 두 초기 대상 또는 종결 대상이 서로 동형(Isomorphic) 관계에 있다는 것을 의미한다는 설명이었다.

말이 조금 어렵게 느껴지지만 조금만 생각해보면 쉽게 이해할 수 있다. 한번 $i_1$ 과 $i_2$ 라는 두 초기 대상이 있다고 가정해보자. $i_1$ 은 초기 대상이니 $i_1$ 에서 $i_2$ 로 향하는 유일한 사상 $f$ 가 존재할 것이다. 마찬가지로 $i_2$ 또한 초기 대상이니 $i_2$ 에서 $i_1$ 로 향하는 유일한 사상 $g$ 가 존재한다. 그렇다면 이 두 사상의 합성은 무엇일까?

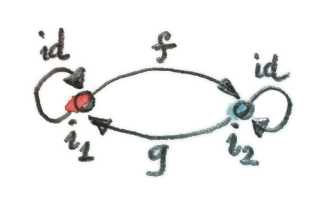이 다이어그램에 존재하는 모든 사상은 전부 유일하게 존재한다.

위 그림을 보면 $f$ 와 $g$ 를 합성한 $g\circ f$ 사상은 $i_1$ 에서 출발해 다시 $i_1$ 로 돌아가는 사상이 된다. 그러나 $i_1$ 은 초기 대상이니 $i_1$ 에서 $i_1$ 로 향하는 사상은 반드시 항등 사상 하나만 존재해야하는데, 모든 카테고리에는 항등 사상이 반드시 존재해야 하기 때문에 이 사상을 제거할 수는 없다. 결국 이러한 제약으로 인해 $g\circ f$ 는 항등 사상일 수 밖에 없는 것이다. 마찬가지로 $i_2$ 에서 $i_2$ 로 향하는 사상도 결국 하나만 존재할테니, $f\circ g$ 도 항등사상이라고 할 수 있다. 이렇게 $f$ 와 $g$ 가 서로의 역이 되어야 한다는 것이 입증됨으로써 어떤 두 초기 대상이든 모두 동형 관계에 놓인다는 사실 또한 증명되었다.

위 증명 과정에서는 초기 대상에서 다시 자기 자신에게 향하는 사상의 유일성을 사용했다. 만약 이 유일성이 보장되지 않는다면 “동형성을 기준으로 유일하다”라는 명제를 증명할 수 없다.

그런데 왜 $f$ 와 $g$ 의 유일성이 필요한걸까? 그 이유는 두 초기 대상이 동형이라는 가정에서 출발하여 초기 대상의 유일함을 증명하기 위해서는 이 동형성마저도 유일하다는 조건이 만족되어야 하기 때문이다. 원칙적으로는 두 대상 간의 여러 개의 동형성이 존재할 수 있겠지만, 이번에 살펴본 예시에서의 두 초기 대상은 서로에게 동형이 될 수 있는 케이스가 단 하나만 존재한다. 이처럼 “유일한 동형성을 기준으로 유일하다”는 것은 보편적 구성의 매우 중요한 특징이다.

5.5 곱(Products)

다음으로 살펴볼 보편적 구성은 바로 곱의 개념이다. 우리는 두 집합의 데카르트 곱(Cartesian Product)이 쌍으로 이루어진 집합이라는 것을 알고 있다. 그렇다면 곱 집합과 곱 집합 내부의 쌍을 이루는 구성 요소 집합들을 연결해주는 패턴은 무엇일까? 우리가 이 패턴을 이해할 수만 있다면 이제 다른 카테고리에도 일반화해서 적용해볼 수 있을 것이다.

💡 역주

만약 집합 $A = \{1, 2\}$ 이고, 집합 $B = \{a, b\}$ 라면 이 두 집합의 데카르트 곱은 $A\times B = \{(1,a),(1,b),(2,a),(2,b)\}$ 와 같이 각 집합의 원소로 구성된 튜플을 원소로 가진 집합으로 정의된다. 즉, 구성 요소 집합이라는 의미는 데카르트 곱 $A\times B$ 의 원소들인 각 튜플을 구성하고 있는 값들의 집합이라는 의미이며, 결국 곱 연산의 재료로 사용된 집합 $A$ 와 집합 $B$ 를 의미하는 것이다.

여기서 역자가 데카르트 곱의 원소가 쌍(Pair)이 아닌 튜플(Tuple)이라고 설명한 이유는, 데카르트 곱이 이항연산이 아니기 때문이다. 즉, 이 연산에는 두 개 이상의 집합이 사용될 수 있으며 데카르트 곱의 원소의 형태도 (x, y, z, …)처럼 계속 길어질 수 있다는 의미이다. 쌍이란 순서가 있는 2개의 구성요소를 가진 개념이고, 튜플은 n개의 구성요소를 가진 개념이므로 엄밀한 정의는 튜플이라고 하는 것이 맞다.

다만 작가는 여기서 “두 집합의 데카르트 곱”이라는 전제를 깔고 있기 때문에 데카르트 곱의 원소들이 $(1,a)$ 와 같은 쌍의 형태라고 말하고 있는 것이다.

일단 우리가 당장 확실하게 이야기할 수 있는 것은 곱 집합에서 각 구성 요소로 향하는 두 개의 함수, 즉 투영 사상(Projections)이 존재한다는 것이다. Haskell에서는 이 두 함수를 fst와 snd라고 부르며, 이 함수들은 각각 쌍의 첫 번째와 두 번째 구성요소를 선택한다.

fst :: (a, b) -> a
fst (x, y) = x

snd :: (a, b) -> b
snd (x, y) = y

이 함수들은 인자를 패턴 매칭하는 형태로 정의된다. 임의의 쌍에 매칭되는 패턴은 위 코드의 (x, y)이며, 최종적으로는 이렇게 매칭된 쌍에 접근하여 각 구성요소를 변수 x와 y로 추출한다.

이 정의는 와일드카드(_)를 사용하면 더 간단하게 표현해볼 수 있다.

fst (x, _) = x
snd (_, y) = y

C++에서 이와 같은 동작은 템플릿 함수를 사용하여 구현해볼 수 있다.

template<class A, class B> A
fst(pair<A, B> const & p) {
    return p.first;
}

이 내용을 토대로 집합의 카테고리에서 두 집합 a와 b의 곱집합을 구성할 수 있는 대상과 사상의 패턴을 정의해보겠다.

이 패턴은 대상 c와 그것을 각각 대상 a와 b에 연결해주는 두 개의 사상 p와 q로 구성된다.

p :: c -> a
q :: c -> b

이 패턴에 부합하는 모든 c는 a와 b의 곱집합의 후보라고 볼 수 있다. 하지만 문제는 이런 후보들이 한두개가 아니라는 것이다.

예를 들어 두 개의 Haskell 타입, Int와 Bool을 a와 b라고 생각하고 이 타입(집합)들에 대한 곱집합 후보를 한번 살펴보자.

자, Int 타입은 Int와 Bool 타입의 곱집합 후보가 맞을까? 맞다. 아래 투영 사상들을 한번 보도록 하자.

p :: Int -> Int
p x = x

q :: Int -> Bool
q _ = True

위 정의는 단순 그 자체이지만, 우리가 정의했던 기준에는 부합한다. 그러면 이번에는 세 개의 구성 요소로 이루어진 튜플인 (Int, Int, Bool)을 살펴보자. 이 튜플 또한 Int와 Bool의 곱집합이 될 수 있다.

p :: (Int, Int, Bool) -> Int
p (x, _, _) = x

q :: (Int, Int, Bool) -> Bool
q (_, _, b) = b

아마도 이미 눈치챘겠지만 우리가 찾아낸 Int와 Bool의 곱집합 후보 중 첫 번째 후보는 곱의 Int 차원만을 다루고 있어 너무 작다고 느껴지고, 두 번째 후보는 Int 차원을 중복시켜놓았으니 너무 크다고 느껴진다.

이제 보편적 구성(Universal Construction)의 랭킹 개념이 등장할 차례이다. 이제 우리는 패턴에 일치되어 뽑힌 두 결과 후보를 비교해볼 수 있을 것이다.

우선 c가 c'보다 “더 나은 경우”를 설명하고 싶은 상황이라고 가정하고, 하나의 후보 대상인 c와 이 대상의 투영 사상 p, q를 다른 후보 대상인 c'와 이 대상의 투영 사상 p', q'와 비교해보려고 한다.

만약 c'에서 c로 향하는 임의의 사상 m이 존재한다면 경우 c가 더 낫다고 말할 수 있겠지만, 그래도 이런 설명은 너무 빈약하다. 우리는 대상 뿐 아니라 이 대상이 가진 투영 사상들에 대해서도 어떤 것이 더 낫다고 설명할 수 있어야하기 때문이다. 즉, 투영 사상 p'와 q' 또한 p와 q, 그리고 사상 m의 합성을 통해 구성될 수 있어야 한다는 의미이다.

p' = p . m
q' = q . m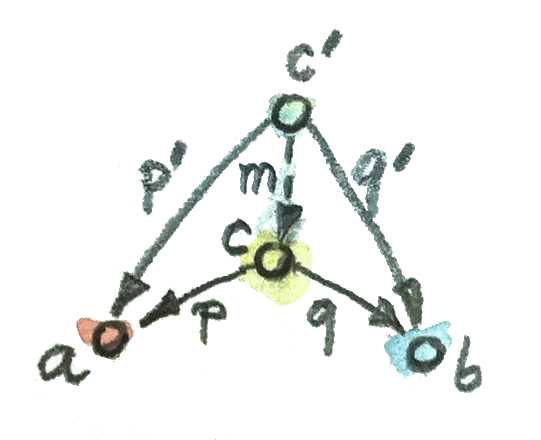

이 방정식을 바라보는 다른 방법은 사상 m이 투영 사상 p'와 q'를 인수분해한다고 보는 것이다. 이 방정식들의 변수들이 함수가 아니라 자연수, 그리고 함수의 합성을 의미하는 점(.)이 곱셉 연산 기호라고 가정해보자. 결국 m은 p'와 q'가 공유하는 공통 인수라는 사실을 알 수 있다.

좀 더 직관적인 이해를 위해, fst, snd 라는 두 표준 투영 사상을 가진 (Int, Bool) 쌍이 앞서 알아봤던 두 개의 후보보다 더 나은 후보가 맞는지를 직접 보여주겠다.

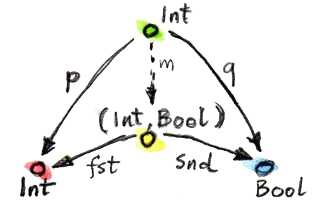
첫 번째 후보를 위한 사상 m은 다음과 같이 정의될 수 있다.

m :: Int -> (Int, Bool)
m x = (x, True)

이때 두 투영 사상 p와 q는 다음과 같이 재구성될 수 있다.

p x = fst (m x) = x
q x = snd (m x) = True

또한 두 번째 후보의 m 또한 아래와 같이 유일한 형태로 결정된다.

m (x, _, b) = (x, b)

이렇게 (Int, Bool)이 다른 두 곱집합 후보보다 더 낫다는 사실을 보였다. 그럼 이제 반대 경우가 성립하지 않는 이유를 살펴보도록 하자. p와 q에서 fst와 snd를 재구성할 수 있는 m’을 찾을 수 있을까?

fst = p . m'
snd = q . m'

첫 번째 곱집합 후보에서 q는 항상 True를 반환했지만, 우리는 이미 두 번째 요소가 False인 쌍 또한 존재할 수 있다는 사실을 알고 있다. 결국 이에 따라 q를 통해 snd를 재구성할 수는 없다는 것을 알 수 있다.

두 번째 예제는 조금 다르다. 두 번째 예제는 p 또는 q 중 하나를 실행한 이후에도 충분한 정보들을 유지하고 있지만, 이번에는 fst와 snd를 인수분해하는 방법이 너무 많다는 것이 문제가 된다.

두 번째 후보의 p와 q는 모두 3개의 구성요소 중 두 번째 요소를 무시하기 때문에 m' 에 어떤 값을 넣어도 전부 말이 된다. 즉 아래와 같은 예시들이 있을 수 있다.

m' (x, b) = (x, x, b)
-- 또는
m' (x, b) = (x, 42, b)
-- 기타 등등...

정리해보자면 어떤 두 투영 사상 p와 q를 가지는 타입 c가 주어졌을 때 이들을 인수분해할 수 있는 m은 유일하게 존재해야하는 후보가 가장 적합한 곱집합 후보라고 볼 수 있다. 사실 이 m은 단순히 p와 q를 하나의 쌍으로 결합하는 녀석이다.

m :: c -> (a, b)
m x = (p x, q x)

이러면 결국 데카르트 곱 (a, b)가 가장 최적의 선택이 되며, 결국 이는 어떠한 두 집합의 곱을 선택하는 것과 동일하므로 이러한 보편적 구성이 집합 카테고리 위에서 제대로 작동한다는 것을 의미한다.

자 이제 집합에 대한 것은 모두 잊어버리고, 동일한 보편적 구성을 이용하여 임의의 카테고리에서 두 대상에 대한 곱을 정의해보도록 하자. 이러한 곱이 항상 존재한다고 말하기는 어렵지만, 만약 존재한다면 독특하게 유일한 동형성(Isomorphism)을 가지게 된다.

👉 두 대상 a와 b의 곱은 “두 투영 사상을 갖춘 대상 c“이며, 다른 “두 투영 사상을 갖춘 대상 c'“에 대해 그 투영 사상들을 인수분해하는 유일한 사상 m이 존재하는 경우를 의미한다.

c와 c' 두 후보로부터 인수분해 사상 m을 생성하는 고차함수는 factorizer라고 불린다. 앞서 살펴본 예시의 경우에는 아래와 같은 함수가 될 것이다.

factorizer :: (c -> a) -> (c -> b) -> (c -> (a, b))
factorizer p q = \x -> (p x, q x)

5.6 합(Coproduct)

카테고리의 모든 구성 요소들과 마찬가지로 곱(Product)에도 대응되는 개념이 존재하는데, 이를 반대곱(Coproduct) 또는 합이라고 한다. 앞서 살펴보았던 곱의 패턴에서 화살표를 반대로 하면 a와 b에서부터 c로 향하는 두 개의 삽입 사상을 가진 대상 c를 만들어볼 수 있다.

i :: a -> c
j :: b -> c

이는 단지 곱의 패턴에서 화살표를 반대로 뒤집은 것 뿐이므로 랭킹 또한 역전된 형태를 띈다. 대상 c가 삽입 사상 i’와 j’를 갖춘 대상 c’보다 더 낫다고 이야기하려면, 삽입 사상을 인수분해하는 사상 m이 존재해야 한다.

i' = m . i
j' = m . j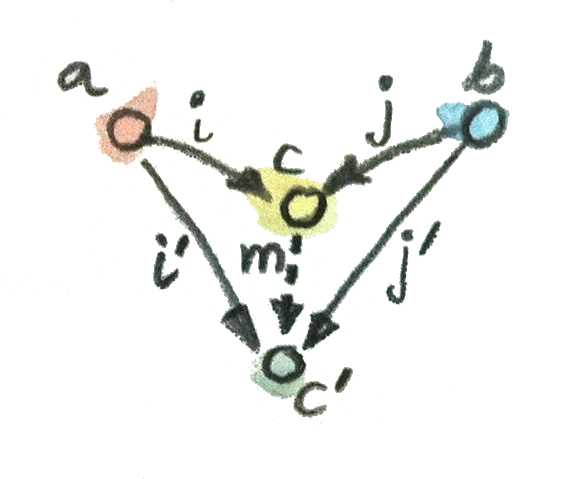

이렇게 찾아낸 가장 잘 들어맞는 대상, 다른 패턴으로 연결되는 유일한 사상을 가지고 있는 대상을 합이라고 하며, 만약 카테고리 내에 합이 존재한다면 이 합은 카테고리 내에서 특정한 두 대상의 결합을 나타내는 유일한 방법을 제공한다는 것을 의미한다.

👉 두 대상 a와 b의 합은 두 개의 삽입 사상을 가진 대상 c로 정의된다. 만약 다른 대상 c' 또한 두 삽입 사상을 갖추고 있다면, c에서 c'로 향하는 유일한 사상 m이 존재하며, 이는 c가 가진 삽입 사상 i와 j를 인수분해한다.

집합의 카테고리에서 합은 두 집합의 서로소 합집합(Disjoint Union)이다. 집합 a와 집합 b의 서로소 합집합의 원소는 모두 a의 원소이거나 b의 원소이다. 만약 두 집합이 겹치는 경우, 서로소 합집합에는 겹치는 부분의 두 복사본이 포함된다. 즉, 서로소 합집합의 원소는 원본을 나타내는 식별자로 일종의 태그가 지정된 것이라고 생각해볼 수 있다.

프로그래머에게는 타입 관점에서 합을 이해하는 것이 더 쉽게 다가올 수 있다. 이는 두 타입의 태그가 지정된 유니온(Tagged Union)이다. C++은 유니온을 지원하지만, 이들은 태그가 없다. 이는 프로그램에서 어떻게든 어떤 유니온 멤버가 유효한지, 어떻게 추적할지 관리해야 한다는 것을 의미한다.

태그가 지정된 유니온을 생성하려면 먼저 Enum(tag)을 정의하고 유니온과 결합해야한다. 예를 들어 int와 char const *의 태그가 지정된 유니온은 아래와 같이 구현해볼 수 있다.

struct Contact {
    enum { isPhone, isEmail } tag;
    union { int phoneNum; char const * emailAddr; };
};

이때 두 삽입 사상은 생성자 또는 함수로 구현할 수 있다. 예를 들어 첫 번째 삽입 사상을 함수 PhoneNum으로 구현해본다면 아래와 같을 것이다.

Contact PhoneNum(int n) {
		Contact c;
		c.tag = isPhone;
		c.phoneNum = n;
		return c;
}

이 함수는 정수를 Contact에 삽입하는 역할을 한다.

이렇게 태그가 지정된 유니온은 때로 변형(Variant)라고도 불리며, boost:variant 클래스 템플릿에서 이러한 변형에 대한 기능을 제공받을 수 있다.

Haskell에서는 수직바(|)로 데이터 생성자를 구분하여 어떤 데이터 형식이든 태그가 지정된 유니온으로 결합할 수 있다. 방금 C++로 만들어본 Contact는 Haskell에서 아래와 같은 선언으로 표현할 수 있다.

data Contact = PhoneNum Int | EmailAddr String

여기서 PhoneNum 과 EmailAddr은 생성자(삽입 사상)와 패턴 매칭에 대한 태그로 사용된다. 아직 잘 이해가 되지 않겠지만 이는 나중에 더 알아보도록 하겠다.

예를 들어 전화번호를 사용하여 연락처를 생성하는 방법은 아래와 같다.

helpdesk :: Contact;
helpdesk = PhoneNum 2222222

Haskell에 기본적으로 내장된 곱의 표준 구현과 다르게 합의 표준 구현은 Either라는 데이터 타입이며, 이는 표준 Prelude에 정의되어있다.

Either a b = Left a | Right b

Either는 a와 b 두 타입을 나타내는 매개변수와 두 생성자를 가진 데이터 타입이다. Left는 a 타입의 값을 나타내며 Right는 b 타입의 값을 나타낸다.

우리가 곱에 대해서 factorizer라는 함수로 정의한 것과 마찬가지로, 합에 대해서도 함수를 정의해볼 수 있다. 후보 대상인 c와 두 후보 삽입 사상 i, j가 주어진다면, Either를 사용하여 함수를 만들어볼 수 있다.

factorizer :: (a -> c) -> (b -> c) -> Either a b -> c
factorizer i j (Left a) = i a
factorizer i j (Right b) = j b

5.7 비대칭성(Asymmetry)

이렇게 쌍대성을 가진 두 개의 집합을 살펴보았다. 종결 대상의 정의는 초기 대상의 정의에서 화살표의 방향을 반대로 하여 얻을 수 있으며, 이와 유사하게 합의 정의는 곱의 정의를 뒤집음으로써 만들어볼 수 있다.

하지만 집합의 카테고리에서 초기 대상은 최종 대상과는 매우 다르며, 합 또한 곱과 다르다. 추후 우리는 곱셈처럼 작동하는 곱집합의 정의에서 종결 대상이 1의 역할을 하고, 덧셈처럼 작동하는 합집합의 정의에서는 초기 대상이 0의 역할을 하는 것을 살펴볼 것이다.

특히 유한 집합의 경우 곱집합의 크기는 개별 집합의 크기를 곱한 것과 같으며, 합집합의 크기는 개별 집합의 크기를 더한 것과 같다. 이는 집합의 카테고리가 화살표의 반전에 대해서 대칭적으로 작동하지 않는다는 사실을 보여준다.

여기서 주의해야 할 점은 공집합이 어떤 집합에 대해 고유한 사상(absured 함수)을 가질 수는 있지만, 이 사상에 대한 역사상은 존재하지 않는다는 것이다. 단일원소집합은 어떤 집합에서 자신에게로 향하는 고유한 사상을 가지고 있지만, 자신에게서 공집합을 제외한 다른 모든 집합으로 향하는 사상 또한 가지고 있다. 종결 대상에서부터 다른 곳으로 향하는 사상은 다른 집합의 원소를 선택하는 매우 중요한 역할을 하지만, 공집합에는 원소가 없기 때문에 선택할 수 있는 것이 없다.

바로 이러한 단일원소집합과 곱집합의 관계가 합집합과의 차별점이다. Unit 타입 () 으로 표현되는 단일원소집합을 곱 패턴의 후보로 생각해보자. 그럼 이제 단일원소집합은 자신으로부터 구성 요소 집합으로 향하는 투영 사상 p와 q를 가지게 된다.

결국 이 두 사상들이 표현하고 있는 행위는 곱집합의 원소를 구성하는 구성요소 중 하나를 선택하는 것이다. 또한 곱집합은 보편적 구성을 따르기 때문에 우리가 정한 후보인 단일원소집합으로부터 곱집합으로 향하는 유일한 사상 m도 존재할 것이다. 이 사상은 곱집합에서 특정 원소, 즉 구체적인 하나의 쌍을 선택할 것이며, 이 사상으로 두 투영 사상을 인수분해할 수도 있다.

p = fst . m
q = snd . m

이를 단일원소집합의 유일한 원소인 값 ()에 대입해보면 위의 식은 아래와 같이 변형될 것이다.

p () = fst (m ())
q () = snd (m ())

여기서 m ()은 사상 m에 의해 선택된 곱집합의 원소이므로 이 식들은 p가 첫번째 집합에서 선택한 요소, 즉 p ()가 m에 의해 선택된 쌍의 첫번째 구성요소와 동일하다는 것을 나타낸다. 마찬가지로 q ()는 두번째 구성요소와 동일할 것이다. 이는 곱집합의 원소가 각 구성 집합의 원소로 이루어진 쌍이라는 개념과 완전히 일치한다.

하지만 합에 대해서는 이렇게 간단한 해석이 불가능하다. 물론 단일원소집합을 합의 후보로 삼아 원소를 추출하려고 해볼 수는 있겠지만, 여기에는 단일원소집합에서 다른 구성요소집합으로 향하는 두 투영 사상이 아니라 다른 구성요소집합에서 단일원소집합으로 향하는 두 삽입 사상이 필요하다. 하지만 이 삽입 사상들은 원본의 정보에 대해 아무것도 알려주지 않을 것이다. 이는 앞서 살펴본 삽입 사상의 factorizer의 구현을 보면 이 함수가 입력된 매개변수 중 하나를 무시하고 있다는 사실에서 알 수 있다. 마찬가지로 합집합에서 단일원소집합으로 향하는 유일한 사상도 아무런 정보를 주지 못한다.

결국 집합의 카테고리는 초기 대상의 방향에서 바라볼 때와 종결 대상의 방향에서 바라볼 때 다르게 보일 수 있다는 것이다. 이것은 일반적으로 수학에서의 집합이 가지는 본질적인 특성이라기보다는 모든 집합이 대상으로 정의되는 카테고리 이론에서 사상으로 사용되는 함수의 특성이다.

함수는 일반적으로 비대칭적이다. 함수는 정의역 집합의 모든 원소에 대해서 정의되어야 한다만, 공역 집합의 모든 원소에 대해 대응될 필요는 없다. 방금 우리는 이러한 함수의 특성 중 극단적인 몇 가지를 살펴본 것이다. 결국 단일원소집합을 정의역으로 가지는 함수들은 공역 집합에서 딱 하나의 원소만 선택하는 함수들이다.

우리는 종종 정의역 집합의 크기가 공역 집합의 크기보다 훨씬 작을 때, 이러한 함수들이 정의역 집합을 공역 집합에 포함시키는 행위라고 생각한다. 예를 들어 우리는 단일원소집합을 정의역으로 가진 함수가 정의역 집합이 가진 단 하나의 원소를 공역 집합에 포함시키는 것이라고 생각할 수 있다. 필자는 이들을 포함 함수(Embedding Functions)라고 부르지만, 수학자들은 이와 반대 시각을 가진 개념을 통해 이름을 부여했다. 이렇게 정의역을 공역에 꽉 채워넣을 수 있는 함수들을 “전사 함수(Surjective Functions)” 또는 “위로의 함수(Onto Functions)”라고 한다.

다른 비대칭성의 원인은 함수가 정의역 집합 있는 여러 원소들을 공역 집합에 있는 하나의 원소로도 매핑할 수 있다는 점이다. 즉 함수는 이러한 원소들을 축소할 수 있다고 보는 것이다. 이에 대한 극단적인 예시는 정의역 집합에 있는 모든 원소를 공역 집합의 단 하나의 원소로 매핑하는 함수들이다. 이전에 보았던 unit :: a -> ()의 정의를 가진 다형적 유닛 함수(Polymorphic Unit Function)이 바로 이 역할을 한다. 이러한 축소 행위는 합성을 통해 더 강화될 수 있다. 두 개의 축소 함수를 합성하는 것은 각각의 개별 함수보다 더 많은 축소 행위를 만들어낼 수 있다. 수학자들은 이렇게 축소되지않는 함수에 대해서 특별한 이름을 붙혔는데, 이를 “단사 함수(Injective Functions)” 또는 “일대일 함수(One-to-one Functions)”라고 부른다.

물론 이렇게 포함도 축소도 아닌 일부 함수들도 존재한다. 이들은 “전단사 함수(Bijection Functions)”라고 불린다. 이 함수들은 전사, 단사 함수와는 다르게 대칭적이며, 이에 따라 역함수도 존재할 수 있다. 집합의 카테고리에서는 동형사상(Isomorphism)이 전단사 함수와 동일한 개념이다.