2024-04-18프로그래밍

[번역] 프로그래머를 위한 카테고리 이론 - 9. 함수 타입

지금까지는 함수 타입의 의미를 간단하게만 설명해왔다. 하지만 조금 더 자세히 들여다보면 함수 타입은 다른 타입과는 약간 다른 특성을 가지고 있다.

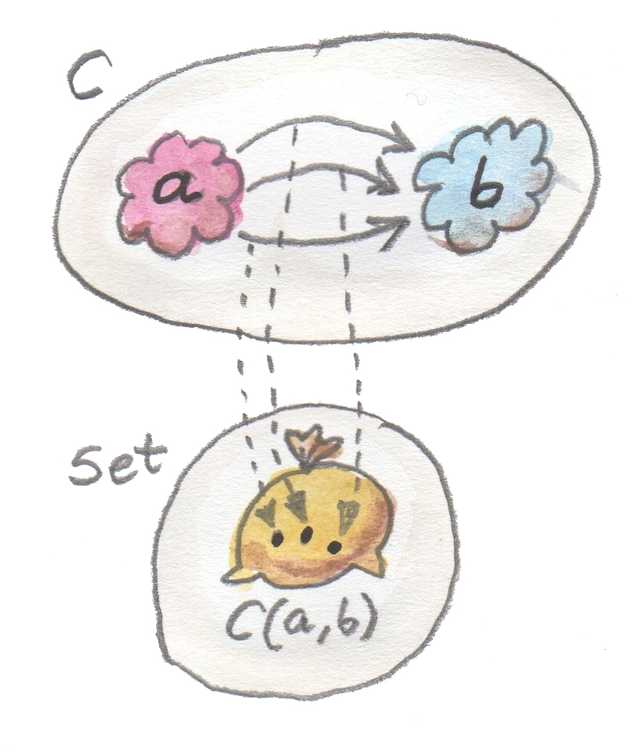
예를 들어 Integer 타입은 그냥 정수들의 집합, 그리고 Bool 타입은 두 개의 원소로 이루어진 집합일 뿐이다. 그러나 함수 타입 a -> b은 대상 a와 b 사이에 존재하는 모든 사상들의 집합이다. 어떤 카테고리에서 두 객체 사이의 존재하는 모든 사상들의 집합은 Hom 집합이라고 한다. 그리고 Hom 집합 또한 결국 집합이기 때문에 카테고리 Set(모든 집합의 카테고리)에서는 Hom 집합 또한 Set에 포함된 대상이다.

Hom 집합도 결국 집합이기 때문에 Set에 포함된 대상이다.

Set이 아닌 다른 카테고리에서는 Hom 집합이 카테고리 외부에 있는 경우도 있다. 이런 경우 외부(External) Hom 집합이라고 한다.

이것이 바로 함수 타입을 다른 타입보다 특별하게 만드는 카테고리 Set의 자기 참조적인 성격이다. 이런 카테고리에서는 Hom 집합을 나타내는 대상을 구성할 수 있는 방법이 존재하며, 이러한 대상을 내부(Internal) Hom 집합이라고 한다.

카테고리 C의 Hom 집합은 외부 Hom 집합이다.

9.1 보편적 구성(Universal Construction)

자, 이제 함수 타입이 집합이라는 사실은 잠시 잊고, 함수 타입을 일반화하여 내부 Hom 집합이라고 생각해서 처음부터 구성해보도록 하자. 일반적으로는 Set 카테고리가 이 구성에 대한 단서를 주겠지만, 여기서는 집합의 특성에 의존하지 않고 생각해볼 것이다. 이런 과정을 통해 하나의 구성이 다른 카테고리에 자동으로 적용될 수 있도록 일반화해볼 수 있다.

함수 타입은 인수 타입과 결과 타입과의 관계로 인해 복합적인 타입으로 간주된다. 이미 우리는 곱 타입과 합 타입이라는 대상 간의 관계를 포함하는 복합적인 타입들을 정의하기 위한 보편적 구성(Universal Construction)에 대해서 배웠던 적이 있다. 함수 타입을 정의하는 데도 동일한 방법을 사용해볼 수 있다.

함수 타입을 정의하기 위해서는 구성하려는 함수 타입, 인수 타입, 결과 타입을 모두 포함하는 패턴이 필요하다.

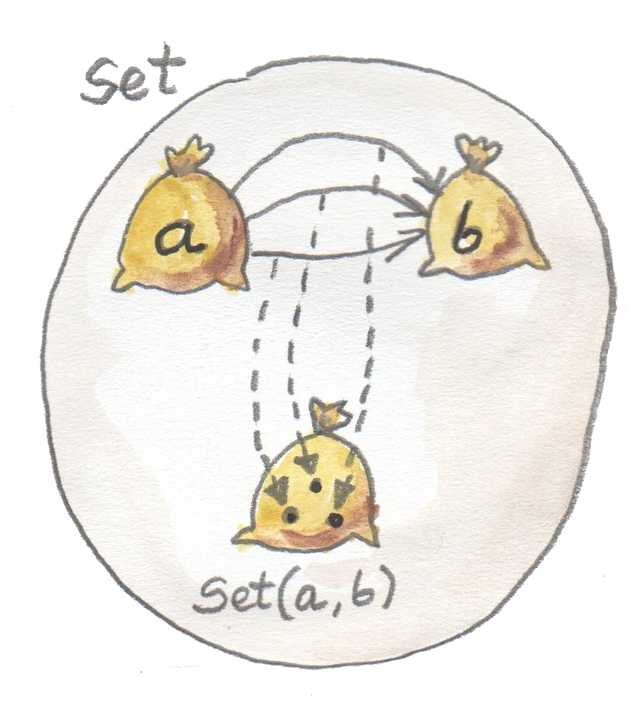
이 세 가지 타입을 연결하는 명확한 패턴은 함수 적용(Function application) 또는 평가(Evaluation)이라고 불린다. 만약 함수 타입의 후보인 대상을 z라고 하고 인수 타입인 대상을 a라고 할 때, 적용(Application)은 이 쌍을 결과 타입인 대상 b로 매핑하는 행위이다. 즉, 우리에게는 총 세 가지 대상이 있으며, 이 중 인수 타입과 결과 타입 두 가지는 고정되어있는 것이다.

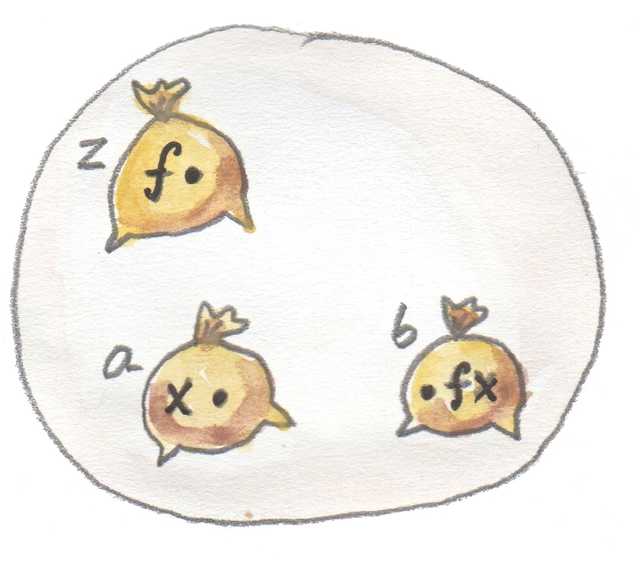
우리는 매핑인 적용도 가지고 있다. 어떻게 하면 이 매핑을 이 패턴에 통합할 수 있을까? 만약 우리가 대상 내부를 들여다볼 수 있다면, 집합 z의 원소인 함수 f와 집합 a의 원소인 인수 x를 짝지어 집합 b의 원소인 f x로 매핑할 수 있게 된다.

함수 집합 z에서 함수 f를 선택하고, 인수 타입 a의 집합에서 하나의 인수 x를 선택한다.
그러면 이제 집합 b에서 원소 f x를 얻을 수 있게된다.

그러나 이렇게 하나의 쌍인 (f, x)를 다루는 것보다는 함수 타입 z와 인수 타입 a의 전체적인 곱에 대해서 이야기하는 것이 더 일반화된 개념일 것이다. 곱 z×a 또한 하나의 대상이며, 이 대상에서 b로의 화살표인 우리의 적용 변형으로 g를 선택할 수 있다. Set에서는 g가 모든 쌍 (f, x)를 f x로 매핑하는 함수가 될 것이다.

두 대상 z와 a의 곱이 사상 g에 의해 다른 대상 b로 연결되는, 이것이 바로 패턴이다.

정말 이 패턴이 보편적 구성을 통해 함수 타입을 명확하게 정의할 수 있는 것일까? 사실 모든 카테고리에 대해서 생각해본다면 그렇지 않을 수도 있다. 하지만 우리가 지금 다루고자 하는 카테고리에 대해서는 충분하다.

그렇다면 또 다른 질문을 해보자. 과연 우리는 곱을 먼저 정의하지 않고도 함수 대상을 정의할 수 있을까? 모든 쌍의 대상에 대해 곱이 없는 카테고리나 모든 쌍의 곱이 존재하지 않는 카테고리도 있지 않은가? 정답은 “아니다”이다. 곱 타입이 없다면 함수 타입도 존재할 수 없다. 이에 대한 내용은 추후 지수(Exponentials)에 대해 설명하며 다시 다루도록 하겠다.

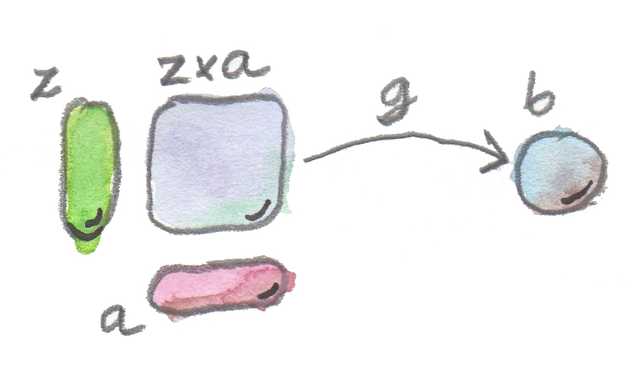이 그림이 바로 보편적 구성의 시작점인 대상과 사상의 패턴이다.

한번 보편적 구성에 대해 검토해보자. 우선 대상과 사상의 패턴에서부터 시작할 것이다. 물론 그저 대상과 사상의 패턴이라고만 하면 굉장히 많은 결과가 매칭될 것이기 때문에 이대로는 상당히 부정확한 쿼리라고 할 수 있다.

Set에서는 거의 모든 것이 서로 연결되어있다. 어떤 대상 z와 대상 a의 곱을 형성할 수도 있으며, 이 곱에서 b로의 함수도 존재할 수 있다. (단, b가 빈 집합일 경우는 제외한다.)

이제 이 패턴의 결과들에 대한 순위를 매긴다는 비밀무기를 꺼내볼 차례이다. 일반적으로 후보 대상들 사이에는 이 구성을 어떤 방식이로든 분해할 수 있는 고유한 매핑이 있어야 한다.

필자는 z와 z×a에서 b로 향하는 사상 g가 z'와 이에 적용되는 사상 g’보다 우수하다고 결정할 것이다. 그리고 만약 이 결정이 참이라면 z'에서 z로 향하는 유일한 사상 h이 존재해야 할 것이다. 그리고 이 사상은 g'를 적용한 결과와 g를 적용한 결과가 동일하다는 것 또한 보장해야한다. (잘 이해되지 않는다면 아래 그림을 보면서 이 문장을 읽어보자.)

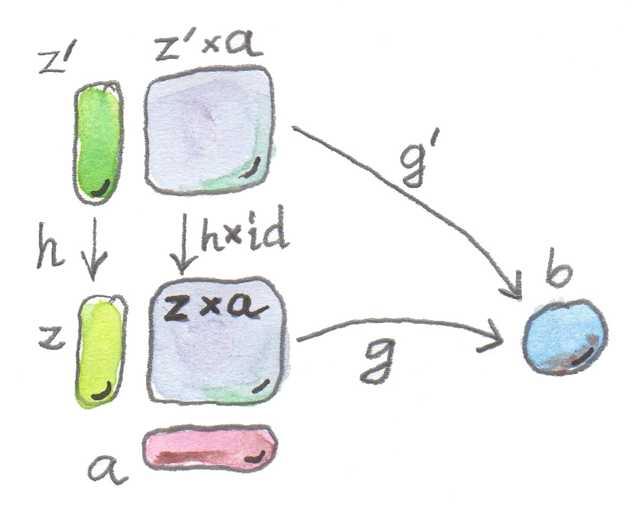함수 대상에 대한 후보들 간의 순위를 결정한다.

여기가 조금 어려운 부분인데, 이게 바로 필자가 이 보편적 구성에 대한 정의를 계속 질질 끌고 있던 이유이다. 사상 h :: z'-> z가 주어졌을 때 우리는 z’와 z가 모두 a와 연결되어있는 다이어그램을 닫기를 원한다.

💡 역주

다이어그램을 닫는다는 이야기가 이해하기 어렵다면, 자료구조 그래프를 떠올려보면 된다. 여기서 z’와 z가 모두 연결되어있는 다이어그램을 닫고 싶다는 의미는, z→a, z’→a, z’→z처럼 연결되어있고 다른 대상들과는 이어지지 않은 그래프를 만들고 싶다는 의미이다.

이를 위해 필요한 것은 z’에서 z로 향하는 매핑 h가 주어졌을 때, 이를 이용해서 z'×a에서 z×a로의 매핑을 얻어내는 것이다. 앞서 곱의 함수적인 특징에 대해 논의했었으니, 이제 이 과정에 대해 이해할 수 있을 것이다.

곱 자체는 펑터, 정확하게는 엔도 이항 펑터이기 때문에 쌍에 대한 사상을 리프팅할 수 있다. 다른 말로 하면 우리는 대상의 곱 뿐만 아니라 사상의 곱도 정의할 수 있다는 것이다.

이를 리프팅하기 위해 곱 z'×a의 두 번째 구성 요소인 a에는 아무런 영향을 끼치지 않아야 하므로, a에 대한 항등사상인 id를 사용하여 사상의 쌍 (h, id)를 리프팅할 것이다.

g’를 g가 포함된 식으로 인수 분해하는 방법은 다음과 같다.

g' = g ◦ (h × id)

여기서의 핵심은 곱이 사상에 대해서 어떻게 작용하고 있는지를 보는 것이다.

보편적 구성의 세 번째 파트는 보편적으로 가장 좋은 대상을 선택하는 것이었다. 필자는 이 대상을 a ⇒ b라고 부를 것이다. (참고로 이건 어떤 대상에 대한 상징적인 이름이며, Haskell 타입 클래스 제약과는 관련없는 네이밍이다. 추후에 조금 더 다양한 방법으로 이름을 지을 수 있는 방법에 대해 논의해보겠다.)

a ⇒ b라는 대상은 (a ⇒ b) × a 에서 b로 향하는 사상인 eval이라는 적용을 가지고 있다. 만약 다른 함수 대상 후보로부터 출발하는 사상 g가 eval을 포함한 식으로 분해되어 이 대상에 유일하게 매핑될 수 있다면, 대상 a ⇒ b가 가장 적합한 후보라고 할 수 있을 것이다.

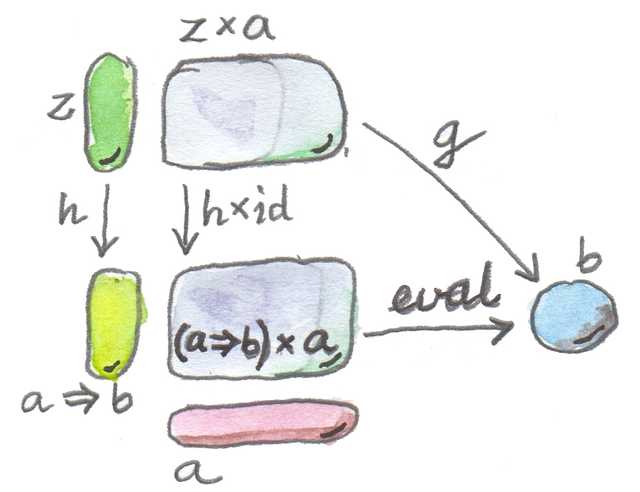이것이 보편적 구성을 통한 함수 대상의 정의이다. 위 그림과 동일한 다이어그램이지만 이제 대상 a ⇒ b가 가장 보편적이게 되었다.

한번 정리해보자.

a에서 b로 향하는 함수 대상은 대상 a ⇒ b와 사상 eval :: ((a ⇒ b) × a) -> b 으로 정의된다. 만약 임의의 다른 대상 z × a에서 b로 향하는 사상 g :: z × a -> b가 주어진다면, z에서 a ⇒ b로 향하는 유일한 사상 h :: z -> (a ⇒ b)이 존재해야하고, 최종적으로 g는 eval을 포함한 식으로 분해될 수 있어야 한다.

g = eval ◦ (h × id)

물론 모든 카테고리에서 반드시 임의의 대상의 쌍 a와 b에 대해 대상 a ⇒ b가 반드시 존재할 것이라는 보장은 없다. 하지만 최소한 Set에서만큼은 항상 존재한다. 게다가 이 대상은 Set의 Hom 집합인 $Set(a,b)$ 와도 동형이다.

9.2 커링(Currying)

함수 대상에 대한 후보를 다시 한번 살펴보자. 그러나 이번에는 사상 g를 두 변수 z와 a에 대한 함수로 생각해볼 것이다.

g :: z × a -> b

대상의 곱으로부터 출발한 사상은 두 개의 변수를 가진 함수와 유사한 형태를 가지고 있다. Set에서 g는 집합 z과 집합 a에서 값을 하나씩 가져와 구성한 쌍에서 출발하게 될 것이다.

그리고 함수 g가 가진 보편적인 속성에 따라 각각의 g에 대해 z를 함수 대상 a ⇒ b로 매핑하는 유일한 사상 h 또한 존재한다는 것을 떠올려볼 수 있다.

h :: z -> (a b)

Set에서는 단순히 h가 타입이 z인 변수를 하나 받아 a에서 b로 향하는 함수를 반환하는 함수임을 의미한다. 이러한 정의는 h를 고차함수(Higher ordered function)로 만든다.

따라서 보편적 구성은 이변수 함수와 함수를 반환하는 일변수 함수 간의 일대일 대응을 설정한다. 이 대응은 커링(Currying)이라고 불리며, h는 g의 커링된(Curried) 버전이라고 한다.

이처럼 어떤 g가 주어졌을때 유일한 h가 존재하고, 어떤 h가 주어질 때도 아래의 공식을 이용하여 이변수 함수인 g를 다시 생성할 수 있기 때문에 일대일 대응이라고 할 수 있다.

g = eval ◦ (h × id)

이때 함수 g는 h의 커링되지 않은(Uncurried) 버전이라고 할 수 있다. 사실 커링은 함수가 함수를 반환하는 Haskell의 구문만으로도 표현할 수 있다.

a -> (b -> c)

이런 문법은 보통 아래와 같이 괄호가 제거된 시그너치를 통해 이변수 함수로 해석된다.

a -> b -> c

이러한 해석은 다인수 함수를 정의할 때 명확하게 확인해볼 수 있다. 예를 들어 아래와 같은 함수처럼 말이다.

catstr :: String -> String -> String
catstr s s' = s ++ s'

이 함수는 하나의 인수를 받아 다시 함수를 반환하는 형태로도 작성할 수 있다. 만약 람다로 표현하면 다음과 같을 것이다.

catstr' s = \s' -> s ++ s'

이 두 정의는 동등하며, 두 정의 중 어떤 것을 사용하든 하나의 인수에 대해 부분 적용되어 아래와 같이 하나의 인수를 받은 함수를 생성할 수 있다.

greet :: String -> String
greet = catstr "Hello "

엄밀히 말하자면 이변수 함수는 곱 타입인 쌍을 받는 함수이다.

(a, b) -> c

이 두 개의 표현 간의 변환은 간단하다. 이미 예상했겠지만 이러한 변환을 수행하는 두 개의 고차함수는 curry와 uncurry로 불린다.

curry :: ((a, b) -> c) -> (a -> b -> c)
curry f a b = f (a, b)

uncurry :: (a -> b -> c) -> ((a, b) -> c)
uncurry f (a, b) = f a b

curry가 함수 대상의 보편적 구성을 위한 인수분해(factorization)라는 점에 주목하자. 이 점은 아래와 같은 형태로 다시 작성해보면 더 명확하게 알 수 있다.

factorizer :: ((a, b) -> c) -> (a -> (b -> c))
factorizer g = \a -> (\b -> g (a, b))

다시 한번 짚고 넘어가자면 factorizer라는 인수분해 행위는 후보로부터 분해 함수를 생성한다.

C++과 같이 함수형 언어가 아닌 언어에서도 커링이 가능하기는 하지만 일이 조금 복잡해진다. C++에서의 다인수 함수는 Haskell에서 튜플을 받는 함수에 해당한다고 볼 수 있다. (여기서 더 혼란스러운 점은 C++에서 명시적으로 std::tuple을 받는 함수, 가변 인수 함수, 초기화 리스트를 받는 함수를 정의할 수 있다는 점이다.)

C++ 함수를 부분 적용하려면 템플릿 std::bind를 사용하면 된다. 예를 들어 아래와 같이 두 개의 문자열을 받는 함수가 있다고 생각해보자.

std::string catstr(std::string s1, std::string s2) {
    return s1 + s2;
}

그럼 이 함수와 std::bind를 사용하여 하나의 문자열을 받는 함수를 정의해볼 수 있다.

using namespace std::placeholders;

auto greet = std::bind(catstr, "Hello ", _1);
std::cout << greet("Haskell Curry");

Scala는 C++이나 Java에 비하면 함수형 프로그래밍에 더 가깝긴 하지만, 사실은 애매한 어딘가에 위치하고 있다. 만약 함수가 부분 적용되도록 작성하려면 아래처럼 여러 인수의 목록으로 정의할 수 있다.

def catstr(s1: String)(s2: String) = s1 + s2

물론 이 코드는 이 함수가 확실히 부분 적용될 것이라는 것을 가정하기 때문에 프로그래머의 예지력에 의존하고 있지만 말이다.

9.3 지수(Exponentials)

수학 논문에서 함수 대상 또는 두 대상 a와 b 사이의 내부 Hom 대상은 종종 지수(Exponential)로 불리며 ba라고 표기된다. 처음에는 이 표기법이 조금 어색해보일 수 있지만, 함수와 곱의 관계를 생각해보면 그렇게 이상한 것도 아니다. 이미 내부 Hom 대상의 보편적 구성에서 곱이 필요하다는 것을 한 차례 확인했지만, 사실 이 둘 간의 연결은 더 심오하다.

이 연결은 Bool, Char, Int, Double과 같이 유한한 값을 가지는 집합 간의 함수를 고려해볼 때 제대로 확인해볼 수 있다. 이러한 함수들은 원론적으로 완전히 메모아이징(Memoizing)될 수 있거나 데이터 구조로 변환되어 조회될 수도 있다. 이것이 바로 사상으로써의 함수와 대상으로써의 함수 타입 간 동등성의 본질이다.

예를 들어 Bool에서의 순수 함수는 False에 해당하는 값과 True에 해당하는 값의 쌍에 의해 완전히 특정화된다. Bool에서 Int로 향하는 모든 함수의 집합은 모든 Int 쌍들의 집합이다. 이것은 곱 Int × Int, 조금 더 창의적으로 표기해보자면 Int2와 동일하다.

다른 예시로 C++의 타입인 char를 한번 살펴보자. 이 타입은 총 256개의 값을 포함하고 있다.

C++ 표준 라이브러리의 isupper, isspace와 같은 일부 함수들은 테이블 조회를 사용하여 구현되며, 이 테이블은 256개의 부울 값들의 튜플과 동등하다. 튜플은 곱 타입이므로 우리는 bool × bool × bool × ... × bool과 같은 256개의 부울의 곱을 떠올려볼 수 있다.

그리고 우리는 이렇게 반복적인 곱이 곧 지수(Exponential)을 정의한다는 사실을 알고 있다. 만약 bool을 char 타입이 가진 값의 개수인 256번만큼 곱한다면, bool을 char만큼 거듭제곱한 것, 즉, boolchar를 얻을 수 있다.

그렇다면 bool의 256 튜플로 정의된 타입에는 얼마나 많은 값이 존재하는 것일까? 정확하게 $2^{256}$ 개이다. 이는 char에서 bool로 향하는 서로 다른 함수들의 개수와도 동일하며, 각 함수는 고유한 256 튜플에 해당된다.

비슷한 방식으로 bool에서 char로 향하는 함수의 개수도 계산해보면 $256^2$ 개라는 사실을 알 수 있다. 함수 타입에 대한 지수 표기법은 이런 의미를 가지고 있는 것이다.

아마 우리는 int나 double에서 출발하는 함수를 모두 메모아이즈하고 싶어하지는 않을 것이다. 하지만 비록 실용적이지 않더라도 함수와 데이터 타입 사이의 동등성은 명확히 존재한다.

그리고 리스트, 트리, 문자열과 같은 무한한 타입도 있다. 이러한 타입에서 출발하는 함수를 메모아이즈하기 위해서는 무한한 저장 공간을 필요로 한다.

그러나 Haskell은 게으른 언어이므로, 게으르게 평가되는 무한한 데이터 구조와 함수 사이의 경계는 모호하게 다가온다. 이러한 함수와 데이터 간의 쌍대성은 함수 타입을 카테고리론적 지수 대상과 동일시 할 수 있다는 것을 설명한다. 이러한 특성은 우리가 가진 데이터에 대한 개념과도 일치하기 때문에 Haskell에서는 함수를 데이터처럼 취급할 수 있다.

9.4 데카르트 닫힌 카테고리(Cartesian Closed Categories)

물론 필자는 계속 집합의 카테고리를 타입과 함수의 모델로 사용할 것이지만, 이런 목적으로 사용할 수 있는 더 큰 카테고리 패밀리가 있다는 것을 언급하는 것은 충분히 가치가 있을 것 같다. 이런 카테고리는 데카르트 닫힌 카테고리(Cartesian closed categories)라고 하며, Set은 그저 이 카테고리 중 하나의 예일 뿐이다.

데카르트 닫힌 카테고리는 아래 세 가지를 반드시 포함하고 있어야 한다.

종결 대상
어떤 두 대상의 곱
어떤 두 대상의 지수

지수를 무한히 많은 횟수로 반복되는 곱이라고 간주한다면, 데카르트 닫힌 카테고리는 임의의 항수를 지원하는 것이라고 생각할 수 있다. 특히 종결 대상은 곱의 항등원(0)인 대상의 곱 또는 대상의 항등원(0) 승이라고 볼 수 있다.

컴퓨터 과학의 관점에서 데카르트 닫힌 카테고리들이 흥미로운 이유는 이 카테고리들이 간단하게 타이핑된 람다 미적분법의 모델을 제공하고 있기 때문이다. 이 모델은 타입을 사용하는 모든 프로그래밍 언어의 기초를 형성한다.

종결 대상과 곱 연산에는 각각 초기 대상과 합 연산이라는 쌍대(Dual)가 존재한다.

a × (b + c) = a × b + a × c
(b + c) × a = b × a + c × a

이 두 요소를 지원하고 곱이 합을 통해 분배될 수 있는 데카르트 닫힌 카테고리를 이중 데카르트 닫힌 카테고리(Bicartesian closed category)라고 한다. 다음 섹션에서 보겠지만 우리가 계속 다뤄온 Set이 대표적인 이중 데카르트 닫힌 카테고리이며, 이 카테고리는 몇 가지 흥미로운 특성을 가지고 있다.

9.5 지수와 대수적 자료형(Exponentials and Algebraic Data Types)

함수 타입을 지수로 해석하는 것은 대수적 자료형의 체계에 아주 잘 들어맞는다. 실제로 고등학교에서 배우는 대수학에서 나오는 숫자 0과 1, 합, 곱, 그리고 지수와 관련된 기본적인 항등식은 각각 초기 대상, 종결 대상, 합집합, 곱집합 그리고 지수에 대해 거의 그대로 적용된다는 것을 볼 수 있다.

우리는 아직 이 성질을 제대로 증명할만한 수반(Adjunction)이나 요네다 보조정리같은 도구를 가지고 있지는 않지만, 그럼에도 불구하고 독자 여러분께 직관을 제공하기 위해 일단 쭉 설명해보겠다.

9.5.1 0승

a^0 = 1

카테고리적 해석에서 우리는 0을 초기 대상으로, 1을 종결 대상으로, 그리고 등식을 동형사상으로 대체한다. 여기서 지수는 내부 Hom 대상을 의미하기 때문에 결국 $a^0$ 이라는 식은 초기 대상에서 임의의 대상 a로 향하는 사상의 집합을 나타낸다. 초기 대상의 정의에 따라 이런 사상은 정확히 하나만 존재할 수 있으므로 Hom 집합 $C(0,a)$ 는 단일 원소 집합이다.

단일 원소 집합은 Set에서의 종결 대상이므로, 이 항등식은 Set에서 쉽게 성립할 수 있다. 여기서 중요한 것은 이 항등식이 이중 데카르트 닫힌 카테고리의 모든 경우에 대해서 성립한다는 것이다.

Haskell에서는 0을 Void로, 1을 유닛 타입인 ()으로 대체한다. 결국 필자가 앞에서 했던 주장은 Void에서 임의의 타입 a로 향하는 함수의 집합이 유닛 타입과 동등하다는 것이다. 다시 말하자면 Void -> a 함수는 하나뿐이라는 것이다. 그리고 우리는 이미 이 함수를 예전에 본 적이 있다. 바로 absurd 함수이다.

그러나 이것을 현실에 구현하기는 약간 까다롭다. 이유는 크게 두 가지인데, 첫째로 Haskell에서는 실제로 어떤 값도 속하지 않는 타입이라는게 존재하지 않는다. 모든 타입은 “끝나지 않는 계산의 결과” 또는 Bottom(_|_)을 포함하기 때문이다.

두번째 이유는 absurd에는 어떤 값도 전달할 수 없기 때문에 누가 무슨 짓을 하던 결국 아무도 실행시킬 수 없다는 점이다. 결국 이 함수의 구현은 근본적으로 모두 동등하다는 것이다. 그렇다고 해서 만약 영원히 끝나지 않는 계산을 전달한다면 이 함수는 결코 반환이라는 행위까지 도달하지 못할 것이다.

9.5.2 1의 지수

1^a = 1

위 식은 Set에서 해석될 때 모든 대상에서 종결 대상으로 향하는 고유한 사상이 존재한다는 종결 대상에 대한 정의를 다시 한번 표현하고 있다. 일반적으로 a에서 종결 대상으로 향하는 내부 Hom 대상은 종결 대상과 동형이다.

Haskell에서 임의의 타입 a에서 유닛으로 향하는 함수는 a -> () 단 하나 뿐이다. 우리는 이 함수를 unit이라고 부른다는 것을 이미 알고 있다. 이 함수는 ()에 부분 적용된 const 함수로 생각할 수도 있다.

9.5.3 1승

a^1 = a

위 식은 종결 대상으로부터 출발하는 사상은 대상 a의 원소를 선택하는데 사용될 수 있다는 것을 다시 표현한 것이다. 이러한 사상들의 집합은 대상 자체와 동형이다. Set, 그리고 Haskell에서는 집합 a의 원소들과 해당 원소들을 선택하는 함수들인 () -> a가 동형이라는 것이다.

9.5.4 지수의 합

a^{b+c} = a^b ×a^c

카테고리론적으로 위 식은 대상의 두 지수의 합이 각 지수를 가진 대상들의 곱과 동형이라는 것을 의미한다.

이 대수적 동형성을 Haskell에서 다루게 되면 매우 실용적인 해석을 가져다준다. 이는 두 타입의 합으로부터 출발하는 함수가 각각의 타입으로부터 출발하는 함수의 쌍과 동등하다는 것을 의미하기 때문이다.

이 개념이 바로 우리가 합에 대한 함수를 정의할 때 사용하는 문법의 근원이다. 우리는 합을 의미하는 Either를 정의할 때 case 문을 사용하여 함수를 정의하지 않고, 각각의 타입 생성자를 따로 처리하는 두 개, 혹은 그 이상의 함수로 나눈다.

예를 들어 합 타입(Either Int Double)를 한번 살펴보자.

f :: Either Int Double -> String

이 경우 Either는 각각 Int와 Double에 대한 함수의 쌍으로 정의될 수 있다.

f (Left n) = if n < 0 then "Negative int" else "Positive int"
f (Right x) = if x < 0.0 then "Negative double" else "Positive double"

9.5.5 지수의 지수

(a^b)^c = a^{b×c}

위 식은 지수 대상들에 대한 커링(Currying)을 표현하고 있다. 함수가 함수를 반환하는 것은 곱에서 출발하는 함수, 즉 이변수 함수와 동등하다.

9.5.6 곱의 지수

(a×b)^c =a^c × b^c

Haskell에서 쌍을 반환하는 함수는 각 쌍의 요소 하나를 생성하는 두 함수의 쌍과 동등하다.

이처럼 고등학교에서 배우는 대수학의 간단한 항등식들이 카테고리 이론으로 확장되어 함수형 프로그래밍에서 실용적으로 적용될 수 있다는 것은 굉장히 놀라운 일이다.

9.6 커리-하워드 동형사상(Curry-Howard Isomorphism)

필자는 이미 논리와 대수적 자료형 간의 대응 관계에 대해 언급한 적이 있다. Void 타입과 유닛 타입(())은 각각 거짓과 참에 해당하며, 곱 타입과 합 타입은 논리곱(AND)과 논리합(OR)에 해당한다. 이 체계에서 함수 타입은 논리적 함의(⇒)에 해당한다. 다시 말해 타입 a -> b는 “만약 a라면 b이다”라고 읽을 수 있다.

커리-하워드 동형사상에 따르면 모든 타입은 참 또는 거짓일 수 있는 명제, 즉 진술이나 판단으로 해석될 수 있다. 해당 타입이 존재하면 그 명제는 참으로 간주되고, 존재하지 않으면 거짓으로 간주된다. 특히 논리적 함의가 참이라는 것은 그에 해당하는 함수 타입이 존재한다는 것을 의미하며, 그 타입의 함수가 실제로 존재한다는 것을 의미한다.

따라서 함수의 구현 자체가 정리의 증명이 되는 것이며, 우리가 프로그램을 작성하는 것은 정리를 증명하는 것과 동등하다. 한번 몇 가지 예시를 살펴보자.

함수 대상의 정의에서 소개했던 eval 함수를 살펴보도록 하겠다. eval의 시그니처는 다음과 같다.

eval :: ((a -> b), a) -> b

이 함수는 함수와 그 인자로 구성된 쌍을 받아 적절한 타입의 결과를 반환한다. 즉 위 코드는 사상에 대한 Haskell에서의 구현이다.

eval :: (a ⇒ b) × a -> b

위 표현은 함수 타입 a ⇒ b (또는 지수 대상 ba)를 정의한다. 이 서명을 커리-하워드 동형사상을 사용하여 논리적 술어로 번역해보자.

((a ⇒ b) ∧ a) ⇒ b

이 명제는 만약 b가 a로부터 도출되는 것이 참이고, a 또한 참이라면, b 또한 반드시 참이어야 한다고 읽을 수 있다. 이는 직관적으로 완벽한 의미를 가지고 있으며 고대부터 전건 긍정(modus ponens)라고 불려왔다. 이제 다음 함수를 구현함으로써 이 정리를 증명할 수 있다.

eval :: ((a -> b), a) -> b
eval (f, x) = f x

a를 받아서 b를 반환하는 함수 f와 타입 a의 구체적인 값 x로 구성된 쌍을 제공한다면, 함수 f를 x에 적용함으로써 타입 b의 구체적인 값을 생성할 수 있다.

즉, 필자는 이 함수를 구현함으로써 타입 ((a -> b), a) -> b가 실제로 존재한다는 것을 보였다. 따라서 우리의 논리에서 전건 긍정(modus ponens)는 참이다.

그렇다면 명백하게 거짓인 술어는 어떨까? 예를 들어 “만약 a 또는 b가 참이면, a는 반드시 참이어야 한다”와 같은 명제가 있다.

a ∨ b ⇒ a

이는 명백하게 잘못된 명제이다. 왜냐하면 이 명제대로라면 a가 거짓이고 b가 참인 상황도 존재할 수 있기 때문이다. 이 술어를 커리-하워드 동형사상을 사용하여 함수 시그니처로 매핑하면 다음과 같은 결과를 얻을 수 있다.

Either a b -> a

사실 아무리 시도를 하더라도 이 함수는 절대 구현할 수 없다. Right 값으로 호출되었을 때는 a 타입의 값을 생성할 수 없기 때문이다. (우리가 순수 함수에 대해서만 이야기하고 있다는 점을 기억하자)

이제 드디어 absurd 함수의 진짜 의미에 대해 이야기할 때가 되었다.

absurd :: Void -> a

만약 Void가 “거짓”이라고 번역된다고 생각해보면 우리는 아래와 같은 술어를 얻을 수 있다.

false ⇒ a

거짓에서는 어떤 것이든 따라올 수 있다(ex falso quodlibet). 여기 Haskell에서 이 명제(함수)를 증명(구현)할 수 있는 한 가지 예시가 있다.

absurd (Void a) = absurd a

Haskell에서 Void는 다음과 같이 정의된다.

newtype Void = Void Void

Void 타입은 까다로운 녀석이다. 이 정의는 Void 타입의 값을 생성하기 위해서는 Void 타입의 값이 필요하다는 의미를 가지고 있기 때문에 절대 값을 구성할 수 없게 만든다. 결국 Void 타입의 값이라는 것은 존재할 수가 없으므로 absurd 함수는 절대 호출될 수가 없는 것이다.

💡 역주

“거짓에서는 어떤 것이든 따라올 수 있다”라는 뜻의 ex falso quodlibet는 거짓 명제로부터는 어떤 명제라도 유도될 수 있다는 것을 의미하며, 이는 논리학에서 매우 중요한 원칙 중 하나이다.

쉽게 말하자면 거짓인 전제가 주어진다면, 그 전제로부터 나오는 어떠한 결론도 모두 정당화될 수 있다는 것이다.이와 마찬가지로 absurd 함수는 절대 생성될 수 없는 값의 타입인 Void를 인자로 받아 임의의 타입 a를 반환할 수 있다고 선언된다.

즉, 거짓으로부터 출발했으니 어떤 타입을 반환하더라도 논리가 깨지지는 않는 것이다.참고로 absurd 함수는 절대 호출될 수가 없기 때문에 실제로 사용될 수는 없고, 순수하게 프로그래밍 언어의 타입 시스템의 원리를 설명하기 위한 이론적인 목적으로만 사용된다.

물론 이 예시들이 모두 흥미롭기는 하지만, 도대체 커리-하워드 동형사상이 우리에게 어떤 실용적인 혜택을 가져다준다는 것일까? 아마도 일상적인 프로그래밍에서는 아니겠지만, Agda나 Coq와 같은 프로그래밍 언어들은 정리를 증명하기 위해 커리-하워드 동형사상을 활용한다.

컴퓨터는 수학자들이 그들의 일을 하는데 도움을 주는 것뿐만 아니라, 수학의 근본을 혁신하고 있다. 이러한 분야에서 가장 최근에 뜨거운 감자로 떠오르는 연구는 호모토피 타입 이론이라고 하며, 타입 이론의 발전에 큰 기여를 하고있다. 이 이론은 Boolean, Integer, 곱과 쌍대곱, 함수 타입 등으로 가득 차 있다. 그리고 이러한 이론은 Coq와 Agda에서 공식적으로 도입되고 있다.

이처럼 컴퓨터는 여러 방면에서 세상을 혁신하고 있다.