수학에서 기원한 프로그래밍 패러다임, 순수 함수

이전에 작성했던 기존의 사고 방식을 깨부수는 함수형 사고 포스팅에 이어, 이번 포스팅에서는 함수형 프로그래밍이 지향하는 관점을 실제 프로그램에 구현하기 위해 알고 있어야하는 필수적인 개념 중 하나인 순수 함수(Pure functions)에 대한 이야기를 해볼까 한다.

2017년 쯤, 함수형 프로그래밍이라는 패러다임이 떠오르면서 순수 함수라는 개념 또한 함께 주목받기 시작했고, 지금도 구글에 순수 함수라고 검색하면 많은 개발자 분들이 순수 함수의 특징에 대한 포스팅을 작성해놓은 것을 볼 수 있다.

일반적으로 우리가 순수 함수에 대해서 공부하려고 하면 다음과 같은 두 가지 특징을 가지는 함수라고 정의하는 경우를 많이 볼 수 있다.

1. 동일한 인풋(인자)에는 항상 동일한 결과를 내야한다.
2. 함수 외부의 상태를 변경하거나, 외부의 상태에 영향을 받아서는 안된다.

그러나 이렇게 공부하게 되면 “순수 함수는 이런저런 특징을 가지고 있는 함수”라고 외우게 되기 쉬운데, 사실 순수 함수는 이렇게 접근할 필요가 없는, 더 심플한 개념이다.

뭐 그냥 이렇게만 외워놔도 순수 함수가 어떤 것인지 이해하고 사용하는 데는 전혀 무리가 없지만, 필자는 순수 함수의 이러한 특징이 어디서 나온 것인지, 순수 함수라는 것이 정확하게 무엇을 의미하는지에 대해 조금 더 근본적인 이야기를 해보려고 한다.

순수 함수는 그냥 수학적 함수다

우리가 순수 함수라고 이름을 붙히고 순수 함수의 특징은 이러이러한 것들이 있다고 공부하기 때문에 뭔가 특별한 함수인 것 같지만, 사실 순수 함수는 그냥 수학에서 사용하는 함수를 프로그래밍의 세계에 똑같이 구현해놓은 것에 불과하다.

위키 백과의 함수형 프로그래밍의 정의를 보면 이 개념에 대해 조금 더 자세하게 작성된 설명을 볼 수 있다.

함수형 프로그래밍(functional programming)은 자료 처리를 수학적 함수의 계산으로 취급하고 상태와 가변 데이터를 멀리하는 프로그래밍 패러다임의 하나이다. 명령형 프로그래밍에서는 상태를 바꾸는 것을 강조하는 것과는 달리, 함수형 프로그래밍은 함수의 응용을 강조한다.

함수형 프로그래밍 - 위키 백과 원문 링크

이 설명에서 가장 중요한 키워드는 바로 수학적 함수라는 단어이다. 우리가 이런저런 특징을 외우며 공부하는 순수 함수라는 녀석은 말 그대로 순수한 함수, 즉 수학에서 사용하는 함수를 의미하는 것이다.

우리가 수학의 세계와 프로그래밍의 세계에서 동일하게 함수라는 개념을 사용하고 있기 때문에 간혹 잊어버리긴 하지만, 사실 프로그래밍에서의 함수는 수학의 그것과는 다른 점이 상당히 많다.

그럼 수학적인 함수와 프로그래밍의 함수 간 차이점을 알아보기 위해, 수학적인 함수의 정의부터 다시 한번 확실하게 짚고 넘어가도록 하자.

수학에서의 함수

우리가 중학생 때 배웠던 함수라는 녀석은 대략 다음과 같은 정의를 가지는 개념이다.

임의의 $x \in X$에 대하여 그에 대응하는 $y \in Y$가 유일하게 존재하는 대응 관계

수학이라는 학문 특유의 어려워 보이는 문법을 사용하긴 했지만 뜯어보면 별 거 없다. 이 정의에서 등장하는 $X$는 정의역, $Y$는 치역이라고 하며, 각각 정의역은 함수의 input, 치역은 함수의 output에 사용될 수 있는 값의 집합이라고 생각하면 된다.

즉, 정의역은 함수의 인자로 사용되는 값들, 치역은 함수의 결과물로 사용되는 값들이라는 뜻이라고 봐도 무방하다.

하지만 이 정의에서 가장 중요한 것은 정의역이니 치역이니 하는 개념이 아니라, 함수의 인자로 사용되는 값 하나에 대응하는 함수의 결과 값이 유일하게 존재한다라는 개념이다.

어떤 값을 함수에 던지면 반드시 하나의 값을 반환하는 것, 이것이 본래 함수의 정의다.

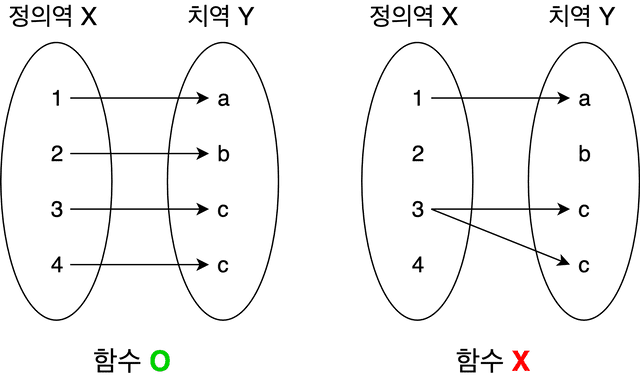오른쪽 그림처럼 정의역의 원소에 대응하는 치역의 원소가 없거나 2개 이상인 경우는
함수의 정의에서 벗어나게 된다

조금 더 편한 이해를 위해 인자로 받은 값에 2를 곱하는 간단한 함수를 생각해보자. 우리는 이런 함수를 정의할 때 $f(x) = 2x$와 같은 식으로 나타낸다.

이제 이 함수의 인자인 $x$를 1이라고 생각해보면 우리는 $f(1) = 2 \times 1 = 2$라는 결과를 얻을 수 있다. 만약 어느 날 갑자기 $f(1) = 3$이 되어버린다면, 이 함수는 특정한 정의역의 원소에 맞대응되는 치역의 원소가 유일하지 않으므로 더 이상 함수라고 부를 수 없는 것이다.

일반적으로 이야기하는 순수 함수의 특징들은 바로 이러한 수학적 함수의 성질에서 기원한다.

프로그래밍에서의 함수

그러나 프로그래밍에서의 함수에는 이러한 제약이 전혀 없다. 이런 저런 예시를 들 것도 없이, 어떤 값도 반환하지 않는 void형 함수가 있지 않은가?

function foo (x): void {
  const y = x * 2;
}

console.log(foo(1));

undefined

수학적인 함수의 정의로 비춰볼 때 이러한 void형 함수는 함수가 아니다. 정의역의 원소인 x와 맞대응하는 치역의 원소가 없기 때문이다. 그래서 프로그래밍에서의 함수라는 개념이 수학의 함수와 약간 다르다고 이야기하는 것이다.

사실 프로그래밍의 함수는 수학의 함수에서 “어떤 값을 던져주면 뭔가를 계산한다”라는 개념만 들고 온 것에 불과하며, 수학적인 관점에서 바라보면 프로그래밍의 함수는 사실 함수가 아닌 경우가 더 많다.

무엇보다 수학의 함수와 프로그래밍에서의 함수가 가장 큰 차이를 보이는 점은 바로 함수의 동작이 일관되지 않을 수 있다는 것이다.

아까 예시로 들었던 $f(x) = 2x$라는 수학의 함수는 내부 구현이 어떻게 되어있던 항상 $x$로 1을 받으면 2를 뱉어내는 것이 보장되어 있지만, 프로그래밍에서는 그렇지 않은 함수도 얼마든지 만들어 낼 수 있다.

예를 들면 Math.random이라던가, Date.prototype.getTime과 같은 메소드들을 사용한 함수 같은 것들 말이다. 이 메소드들은 함수의 동작과 전혀 상관없는 값을 만들어내기 때문에, 함수의 연산이 이러한 값들에 종속되어 버린다면 개발자는 이 함수가 어떤 값을 뱉어낼 지 절대 예측할 수가 없다.

function sum (x: number): number {
  return x + Math.random();
}

sum(1);
sum(1);
sum(1);

5 // ?
4 // ?
9 // ?

이런 개념은 특정한 의미를 가지는 값들을 저장, 할당, 호출할 수 있는 프로그래밍의 세계에서만 존재하는 것들이며, 수학의 세계에서는 이런 개념 자체가 없다.

이렇게 특정한 의미를 가지는 값들을 우리는 상태(State)라고 부른다. 상태는 프로그램의 현재 상황을 보여주는 좋은 역할도 하지만, 여기저기서 무분별하게 이 상태를 참조하거나 변경하는 경우, 개발자조차 현재 프로그램이 어떻게 돌아가는지 파악하기 힘든 슬픈 상황이 발생할 수도 있다.

그래서 개발자들은 상태를 변경하는 행위에 특정한 규칙과 제약을 정해서 무분별한 상태 변화를 최대한 피하고, 이런 변화를 추적할 수 있는 상황을 선호한다.

문제는 프로그래밍에서의 함수는 이런 상태들, 더 정확히 이야기하자면 함수 외부의 상태들과 뭔가 썸씽이 생기는 경우가 많다는 것이다. 여기 인자로 받은 수를 함수 외부에 선언된 변수와 더한 후 반환하는 addState라는 간단한 함수가 있다.

let state = 3;
function addState (x: number): number {
  return state + x;
}

addState(1);

4

addState 함수는 자신 외부에 있는 state라는 값을 참조하여 자신이 인자로 받은 수를 더해주는 간단한 일을 한다.

즉, 이 함수의 결과 값은 함수의 외부 상태인 state 변수에 종속되어 있다는 것이며, 이런 상황은 개발자가 함수의 동작을 예측할 수 없게 만드는 위험 요소로 작용할 수 있다.

만약 다른 곳에서 state 변수의 값을 변경이라도 하면 상황은 더욱 꼬이기 시작할 것이다.

state = 10;
addState(1);

11

이전과 같은 함수에 같은 인자를 사용했지만, 결과값은 전혀 다르게 나왔다. 이 함수는 외부 상태의 변화에 따라 자신의 결과 값도 변경되기 때문에, 개발자는 이 함수의 동작을 전혀 예측할 수 없는 것이다.

이렇게 함수가 함수 외부 상태에 영향을 받거나, 함수 외부 상태를 직접 변경하는 행위를 사이드 이펙트(Side Effect)라고 하며, 사이드 이펙트를 발생시키는 함수는 개발자가 예측하지 못한 버그를 발생시키는 위험 요소 중 하나이다.

그런 이유로 자바스크립트와 같은 언어에서는 전역 변수의 선언 및 할당을 최대한 지양하는 컨벤션을 내놓기도 하며, React Hooks에서는 사이드 이펙트를 발생시키는 동작을 따로 구분하기 위해 useEffect라는 훅을 제공하기도 한다.

function TestComponent () {
  useEffect(() => {
    localStorage.setItem('greeting', 'Hi');
    return () => {
      localStorage.removeItme('greeting');
    };
  });

  return <div>TestComponent</div>;
}

지금 이게 간단한 함수인데다가 의도적으로 연출한 상황이라 부자연스러워 보일 수도 있지만, 실제 어플리케이션에는 이거보다 훨씬 복잡하고 이상한 짓들을 하는 함수가 수두룩하다.

예를 들면 API 서버와 통신한 결과물을 뱉어내는 간단한 함수 또한 순수하지 않은 함수의 일종이다.

async function getUsers () {
  try {
    const response = await fetch('/api/users');
    return response.json();
  }
  catch (e) {
    throw e;
  }
}

딱 봐도 getUsers는 호출할 때마다 항상 같은 값을 반환하는 함수는 아니다. 현재 데이터베이스의 상태에 따라 유저 리스트는 매번 달라질 수 있기 때문이다.

이렇게 순수하지 않은 함수는 개발자가 함수의 결과를 예측하는 것이 불가능하기 때문에, 함수의 동작을 검사하는 테스트를 작성하는 것 또한 불가능하다. 애초에 아웃풋으로 뭘 내보낼 지도 감이 안오는 변덕스러운 녀석을 어떤 기준으로 검사한단 말인가?

이렇듯 프로그래밍의 세계에서 이야기하는 함수는 수학의 함수보다 더 변수가 많고, 결과를 예측하기가 힘든 개념이다.

순수한 수학적 함수로 회귀하자

자, 이제 수학의 세계에서 말하는 함수와 프로그래밍의 세계에서 말하는 함수의 차이를 살펴보았으니, 다시 순수 함수의 정의를 가져와보자.

1. 동일한 인풋(인자)에는 항상 동일한 결과를 내야한다.
2. 함수 외부의 상태를 변경하거나, 외부의 상태에 영향을 받아서는 안된다.

앞서 이야기 했듯이, 수학의 세계에서 함수는 단순히 인풋을 받으면 뭔가 계산을 해서 단 하나의 결과를 내는 개념이다.

그리고 수학의 세계에는 뭔가 값을 저장해놓고 할당도 하고 호출할 수도 있는 상태라는 개념이 없으니, 함수가 함수 외부 상태에 영향을 주고 받는 사이드 이펙트라는 것도 당연히 존재할 수가 없다.

즉, 수학에서의 함수를 프로그래밍에 그대로 적용하면 순수한 함수의 특성인 “함수의 결과는 함수의 인자에만 영향을 받는다”라는 조건과 “함수 외부의 상태를 변경하거나 영향을 받아선 안된다”라는 조건이 자연스럽게 충족되는 것이다.

그리고 함수형 프로그래밍에서 이야기하는 불변성(immutable) 또한 수학과 맞닿아 있는 지점인데, 애초에 상태라는 개념이 존재하지 않는 수학의 함수를 프로그래밍으로 구현한 순수 함수를 사용하고 있으니, 상태를 변경한다는 개념 또한 없어야 하는 것이다.

하지만 프로그래밍의 세계에는 엄연히 상태라는 개념이 존재하기 때문에, “함수의 인자를 직접 수정해서는 안된다”와 같은 제약들을 스스로 정의하고 지켜나갈 수 있도록 저런 개념을 명시적으로 이야기하는 것이다.

또한 순수 함수를 사용함으로써 따라오는 장점들인 “테스트가 쉬워진다”, “참조 투명성이 보장된다”와 같은 이야기들도 수학적인 개념에서의 함수를 생각하면 사실 당연하기 그지 없는 이야기들이다.

앞서 잠깐 이야기 했지만, 매번 다른 값이 나오는 함수에 대한 유닛 테스트를 짠다고 생각해보면 진짜 답이 없다. 애초에 개발자가 함수의 동작을 예측할 수 없으니 함수의 동작에 대한 모법 답안을 제시할 수도 없을 것이고, 당연히 테스트 작성도 불가능 하다.

또한 순수 함수를 사용하면 참조 투명성이 보장된다는 말도 결국 우리가 수학에서 사용하고 있는 = 기호의 의미를 생각해보면 그렇게 특별한 말이 아니다.

이렇듯 순수 함수는 어떤 인자를 사용했을 때 어떤 결과 값이 나올 지 동작을 예측할 수 있고, 상태라는 것을 아예 없애버린 개념이기 때문에, 개발자가 예측 가능한 어플리케이션을 개발하기 쉽게 만들어준다.

또한 함수 자체가 함수 외부의 상태와 관계 없이 순수하게 단일한 연산에만 집중하고 있으니, 한 어플리케이션에서 선언한 순수 함수는 다른 어플리케이션에다가 가져다 붙혀도 반드시 동일한 동작을 한다는 것이 보장된다. 즉, 좋은 모듈화의 조건 중 하나인 높은 응집도에도 부합한다.

이렇게 순수 함수를 사용하여 작성된 어플리케이션은 개발자가 구조와 동작을 쉽게 이해할 수 있기 때문에, 굳이 함수형 프로그래밍 패러다임이 아니더라도 전반적인 어플리케이션 설계에 꽤나 도움이 되는 개념이라고 할 수 있다.

마치며

필자는 처음 순수 함수라는 개념을 접했을 때 구글링과 다른 분들이 작성해주신 포스팅들을 통해 순수 함수의 특징, 장점, 단점 등을 먼저 접하게 되었는데, 당시에는 “또 새롭게 공부할게 나왔구만”이라는 생각이었다.

또 새로운 공부거리가 생겨버렸네...

사실 순수 함수와 같은 패러다임을 처음 접하게 되면 습관처럼 구글링을 통해 정보를 습득하고 공부를 하게 되는데, 이때 일반적으로 다른 사람들이 정리해놓은 포스팅을 보고 공부하게 되는 경우가 많았다.

그러나 이렇게 공부를 하는 경우, 해당 패러다임의 근본적인 발생 이유나 원리에 대해서 깊이 파악하기 보다는 몇 가지 특징이나 장단점을 먼저 학습하게 되는 경우가 많았던 것 같다.

그래서 순수 함수도 “새롭게 공부해야하는 것”이라는 느낌으로 받아들였었지만, 나중에 곰곰히 생각해보니 그냥 어릴 때 배웠던 수학적인 함수의 개념을 그대로 프로그래밍으로 구현한 것이라는 개념이라는 것을 깨닫고 꽤나 허무했던 기억이 있다.

그래서 필자는 이 포스팅에서 “순수 함수는 이런저런 특징을 가진 함수”라고 설명하지 않았던 것이다. 개인적인 생각이기는 하지만, 대부분의 사람들은 어릴 때 이미 학교에서 함수에 대한 정의와 개념을 학습했기 때문에, “수학적인 함수”라는 키워드로 접근하는 것이 오히려 이해가 빠를 것이라고 생각했다.

어쨌든 필자는 이 포스팅을 통해 순수 함수는 전혀 새로운 개념이 아니라는 이야기를 하고 싶었고, 대한민국 의무 교육을 받은 사람이라면 누구든지 다 익숙하게 받아들일 수 있는 개념이라는 것을 이야기하고 싶었다.

물론 순수 함수를 사용하여 어떤 식으로 프로그램을 설계하는 것이 훌륭한 설계인지와 같은 이야기는 의무 교육과정에 없기 때문에 별도로 공부를 해야겠지만, 적어도 함수형 프로그래밍에서 중요한 키워드로 이야기하고 있는 순수 함수와 불변성에 대한 이해 정도는 그렇게 어려운 것은 아닐 것이라고 생각한다.

다음 포스팅에서는 순수 함수와 함께 함수형 프로그래밍에서 중요한 개념 중 하나인 불변성에 대한 이야기를 해보려고 한다.

이상으로 수학에서 기원한 프로그래밍 패러다임, 순수 함수 포스팅을 마친다.

• 순수 함수는 그냥 수학적 함수다

  • 수학에서의 함수
  • 프로그래밍에서의 함수
• 순수한 수학적 함수로 회귀하자
• 마치며