수학과 함께 복잡한 문제를 단순하게 만들자
수학이 어렵다고? 패턴만 봐도 문제 해결이 쉬워진다
최근 많은 IT 기업들이 개발자를 채용할 때 코딩 테스트를 시행하고 있다. 회사마다 어떤 스타일의 문제를 출제하는지 차이는 있지만, 대부분 간단한 알고리즘 풀이 또는 Codility나 프로그래머스와 같은 사이트처럼 실무에서 겪을 만한 상황을 살짝 섞어놓는 느낌의 문제를 선호하는 것 같다.
이런 문제들의 특성 상 CS 기초와 문제 분석 능력, 직감 등을 다양하게 사용하여 해결해야 하기 때문에 단기간 연습한다고 실력이 확 느는 것은 아닌 것 같다.
이런 문제들은 우리에게 단순히 “너 이 알고리즘 알아?”라고 물어보는 것이 아니라 “어떤 방법을 사용해서 풀어볼래?”라고 물어본다.
사실 자료구조나 알고리즘 자체는 보면 공부하고 몇 번 구현해보면 어느 정도 숙달될 수 있지만, 이렇게 문제를 분석하고 단순화해서 적합한 방법을 선택할 수 있는 능력은 단순히 공부로 만들어 낼 수 있는 종류의 것은 아닌 것 같다.
필자는 최근 취업 준비를 하면서 이런 문제를 종종 풀어보고 있는데, 확실히 CS 기초도 부족하긴 하지만, 문제를 분석하고 좋은 방법을 선택할 수 있는 능력이 많이 부족함을 느꼈다.
그래서 자료구조나 알고리즘을 처음부터 다시 공부하면서, 동시에 문제 해결 능력을 기르기 위한 방법이 어떤 것이 있을지 고민해보기 시작했다.
수학적인 사고 방식으로 문제를 단순화하자
필자는 최근 면접에 거하게 털리고 나서 CS 기초나 자바스크립트 기초를 처음부터 다시 공부하기 시작했는데, 막상 이렇게 공부한 지식을 가지고 코딩 테스트 문제를 한번 풀어보려고 했더니, 생각처럼 잘 되지 않았다.
대부분 알고 있겠지만, 많은 코딩 테스트 문제은행 서비스에서는 문제를 해결하고 나면 다른 사람들은 이 문제를 어떤 방식으로 해결했는지도 함께 보여준다. 필자같은 경우는 사실 이게 궁금해서 문제를 푸는 것도 있는 것 같다.
그러던 와중에 대부분의 사람들이 완전탐색으로 풀었던 문제를 어떤 굇수 분이 단순한 산수 연산 몇 번으로 풀어내는 것을 본 적이 있었다.
 역시 세상은 넓고 굇수는 많다
역시 세상은 넓고 굇수는 많다
당연히 필자도 해당 문제를 완전탐색으로 풀었고 그 방법 밖에 없을 것이라고 생각했지만, 그 굇수분은 문제의 패턴을 찾아내어 문제를 단순화 시킨 것이다.
물론 조금 난해한 감이 있어서 실무에서 사용하기에는 조금 이견이 갈릴 수 있는 코드이긴 했지만, 대부분의 사람들이 완전탐색으로 풀었던 복잡한 문제를 단순한 식 몇개로 풀어냈다는 사실이 충격이었다.
이때 필자가 느낀 점은 바로 수학적인 사고에 대한 필요성이었다. 물론 알고리즘 역시 이런 수학적인 사고를 바탕으로 효율적인 해결 방식을 일반화한 것이긴 하지만, 필자가 원했던 것은 좀 더 근본적인 문제 해결 능력이었다.
물론 수학적인 사고라고 해서 문제를 읽고 막 복잡한 식을 세우는 것이 아니다. 자연어로 이루어진 문제를 분석하고, 해결 가능한 수준으로 나누고, 패턴을 찾아내는 과정 또한 수학적인 사고에서 비롯된다. 애초에 수학 자체가 복잡한 문제를 단순화하고 패턴을 찾아내어 일반화하는 학문이다.
그리고 개발자는 수학을 잘해야할까? 포스팅에서 한번 이야기한 적 있지만, 필자가 이야기하고싶은 수학은 어려운 이론이나 공식을 말하는 것이 아니다.
개인적인 생각이기는 하지만, 필자는 “수의 성질”을 이해하는 것이 제일 중요하다고 생각했다. 예를 들면 홀수에 1을 더하면 짝수가 된다던가, 1부터 100까지의 합을 구할 때 101 * 100 / 2를 하면 된다던가와 같은 것들이 그렇다.
그런 이유로 최근 프로그래머, 수학으로 생각하라라는 책을 읽게 되었는데, 이 책의 초입부부터 재미있는 문제 해결 방법이 몇개 나와서 그 문제들과 해결 방법에 대해서 공유를 해볼까 한다.
오늘로부터 100억일 후는 무슨 요일일까?
일 후의 요일을 구하는 문제는 수학적인 사고를 필요로 하는 대표적인 문제 중 하나이다.
게다가 굳이 코딩 테스트까지 가지 않고 일상 속에서 비즈니스 로직만 만지고 있더라도 꽤나 자주 접할 수 있는 문제이다. 그래서 워밍업으로 상대적으로 익숙한 요일 구하기 문제를 먼저 살펴보려고 한다.
필자가 이 글을 작성하고 있는 2019년 10월 29일은 “화요일”이다. 그럼 오늘로부터 100억일 후는 과연 무슨 요일일까?
음, 단순하게 생각해보면 오늘은 화요일이니까 1일 후는 수요일, 2일 후는 목요일과 같은 순차적인 방법으로 접근할 수도 있겠다.
console.time('calc');
const week = ['일', '월', '화', '수', '목', '금', '토'];
let today = 2;
let shift = 0;
for (let i = 0; i <= Math.pow(10, 10); i++) {
shift = i % week.length;
}
today += shift;
if (today > week.length - 1) {
today -= week.length;
}
console.log(week[today]);
console.timeEnd('calc');토
calc: 60948.138ms아무리 요즘 컴퓨터가 연산 능력도 좋고 무보수로 일해주는 SCV라고 하지만 100억회를 반복하는 루프를 계산하게 하는 것은 너무나도 가혹한 처사이다. 이 알고리즘은 시간 복잡도가 이기에, 루프만 돌았을 뿐인데도 수행 시간이 1분이 넘는다.
이렇게 무식하게 풀어낼 수는 없으니, 다른 방법을 찾아야한다. 다행히 우리는 요일이 7일 마다 반복된다는 것을 알고 있다. 오늘이 화요일이라면 7일 후도 당연히 화요일이고, 14일 후도 화요일이다.
즉, 요일이 반복된다는 “주기성”이 존재한다는 것이다. 오늘부터 7의 배수만큼 지난 날은 무조건 화요일이라는 패턴을 찾았다면 그 다음부터는 간단해진다.
어떤 수를 1씩 증가시켜가면서 계속 7로 나누면 0 - 6이 순차적으로 나타나는 주기성이 있으므로, 배수를 구할 때와 마찬가지로 100억을 7로 나누고 그 나머지를 확인하면 되기 때문이다.
console.time('calc');
const week = ['일', '월', '화', '수', '목', '금', '토'];
let today = 2;
const shift = Math.pow(10, 10) % week.length;
today += shift;
if (today > week.length - 1) {
today -= week.length;
}
console.log(week[today]);
console.timeEnd('calc');토
calc: 0.156ms수행 시간이 60000ms에서 0.156ms로 줄었다. 이렇게 문제에서 주기성을 찾아내고, 나머지의 주기성과 연관지을 수만 있다면, 완전탐색을 하지 않고도 나머지를 사용하여 문제를 가볍게 풀 수 있다.
일 후의 요일도 구해보자
자, 그럼 여기서 한번 더 나아가보자. 이런 방법으로 우리가 일 이후의 요일도 구할 수 있을까? 10의 1억승을 뭐라고 부르는지는 모르겠지만, 관측 가능한 우주의 모든 원자 개수가 약 개 정도라고 하니 이 어마무시하게 큰 수인 것은 분명하다.
당연히 은 자바스크립트의 Number.MAX_SAFE_INTEGER 값을 아득히 넘어서는 숫자이기 때문에 위와 같은 방식으로는 계산이 불가능 하다. 여기서부터는 컴퓨터한테 계산을 맡기는 것보다는 문제를 단순화하고 주기성을 찾아내는 일이 더 중요해진다.
오늘은 10월 29일 화요일이니 오늘부터 일 후의 요일을 쭉쭉 살펴보도록 하자. 방금 예제로 만들었던 로직을 활용하여 일 이후까지 살펴보니, 대략 다음과 같은 패턴이 있다는 것을 알 수 있었다. 모든 결과를 적으면 너무 표가 길어지니, 일 이후의 결과만 기재하도록 하겠다.
| 일자 | 요일 | 인덱스 |
|---|---|---|
| 일 후 | 수 | 3 |
| 일 후 | 금 | 5 |
| 일 후 | 목 | 4 |
| 일 후 | 월 | 1 |
| 일 후 | 토 | 6 |
| 일 후 | 일 | 0 |
| 일 후 | 수 | 3 |
| 일 후 | 금 | 5 |
| 일 후 | 목 | 4 |
| 일 후 | 월 | 1 |
| 일 후 | 토 | 6 |
| 일 후 | 일 | 0 |
| 일 후 | 수 | 3 |
필자는 이 과정에서 두 가지 정보를 얻을 수 있었다. 요일이 수, 금, 목, 월, 토, 일의 순서로 계속 반복되고 있다는 것과 오늘 요일인 화요일이 등장하지 않는다는 것이다.
즉, 10의 지수가 6 증가할 때마다 같은 요일이 돌아온다. 바꿔말하면 0의 개수가 6개씩 늘어날 때마다 같은 요일이 돌아온다는 말과 같다.
그렇다면 결국 10의 지수를 6으로 나눈 나머지 값을 사용하여 방금 전과 동일한 방법으로 요일을 구할 수 있다는 말이다.
const week = ['수', '금', '목', '월', '토', '일'];
const exp = Math.pow(10, 8);
console.log(week[exp % week.length]);토비록 이라는 어마무시한 수를 컴퓨터가 담아낼 수 없기 때문에 직접 계산할 수는 없지만, 지수의 증가로 인한 요일의 주기를 파악함으로써 상상도 안가는 먼 미래의 요일을 구할 수 있게 되었다. (사실 이걸 구하는 게 뭔 의미가 있겠냐만…)
만약 위에서 요일을 구했던 정직한 방법으로 이 문제를 풀려고 했다면 불가능했겠지만, 문제를 분석하고 주기성을 찾아냄으로써 어찌어찌 풀 수는 있었다.
욕실 바닥에 타일 깔기
사실 방금 풀어보았던 요일 맞추기 문제처럼 눈에 띄게 일정한 주기를 가지고 반복되는 숫자를 찾아내는 문제는 익숙해지는데 그렇게 오랜 시간이 걸리지는 않는다.
그러나 우리가 일상에서 겪는 대부분의 문제는 저렇게 패턴을 대놓고 보여주지 않는 경우가 많다.
이때 필요한 것이 문제를 분석하고 패턴을 찾아내는 일이다. 사실 주기성이라는 수의 성질을 이용할 수 있다는 것의 진짜 의의는 바로 패턴을 만들고 찾아낼 수 있다는 것에 있다. 이번에는 그 패턴을 이용하여 유효성을 검사하는 문제이다.
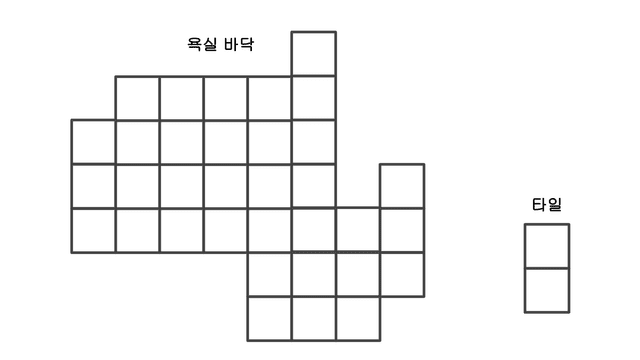
에반은 타일 시공 업체에 취직해서 첫 욕실 바닥 시공을 하게 되었다. 그러나 오늘이 첫 출근인 에반은 실수로 가로 1cm, 세로 2cm의 직사각형 타일들만 챙겨나와버린 상황.
다행히 모든 욕실 바닥은 표준화가 되어있어서 가로 1cm, 세로 1cm의 정사각형 칸으로 이루어져있지만, 욕실 바닥 모양과 칸의 수는 모두 제각각이다.
에반은 자신의 직사각형 타일로 욕실 바닥을 빠짐없이 메꿔야하지만, 욕실 바닥의 모양에 따라 작업이 불가능한 곳도 있다. 게다가 에반은 힘이 없어서 타일을 반으로 쪼개서 사용할 수도 없다.
에반은 어떻게 작업의 가능 여부를 알 수 있을까?
const floor = [
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 1, 1, 1, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 1, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 1, 1, 1, 1],
[0, 0, 0, 0, 1, 1, 1, 0],
];이 문제의 경우, 타일로 욕실 바닥을 채울 수 있는 경우의 수를 하나씩 검사해볼 수도 있겠지만, 그렇게 풀어내기에는 워낙 경우의 수가 많기도 하고 로직도 복잡해질 것이 뻔하다.
그렇다면 욕실 바닥에 있는 칸의 개수를 세어보면 어떨까? 타일은 두 칸이 한 세트이기 때문에 만약 바닥 칸의 개수가 홀수라면 에반이 가진 타일로는 절대 바닥을 채울 수가 없을 것이다.
하지만 이 문제에 나와있는 바닥의 총 칸 수는 슬프게도 짝수인 34칸이기도 하고, 어차피 바닥 칸의 홀짝 여부를 알아내는 것만으로 이 문제를 해결할 수는 없다. 조금 더 확실한 검증 방법이 없을까?
이 문제는 주기성과 전혀 관련이 없을 것 같지만, 사실 굉장히 간단한 패턴이 숨어있다. 바로 에반이 가지고 있는 타일이 두 개의 칸으로 이루어져 있다는 것이다.
조금 더 생각을 쉽게 하기 위해 타일과 바닥에 색을 칠해보도록 하자.
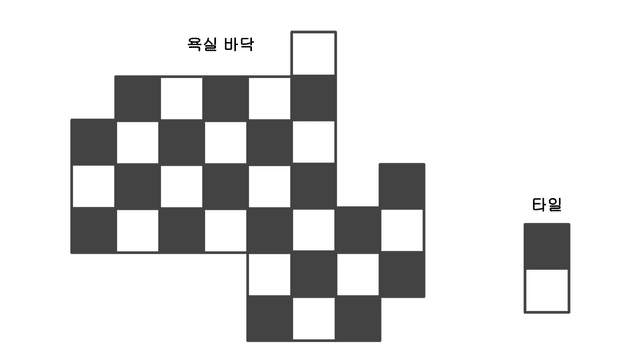
이렇게 색을 칠하고나니 에반이 가지고 있는 타일은 검은색 1칸과 흰색 1칸으로 이루어진 두 칸짜리 타일이 되었다. 즉, 만약 에반이 가지고 있는 타일로 욕실의 바닥을 빈틈없이 메꿀 수 있다면, 욕실 바닥의 검은색 칸의 수와 흰색 칸의 수가 같아야 한다는 것이다.
그러나 우리에게 주어진 욕실 바닥의 검은색 칸의 수는 16칸, 흰색 칸의 수는 18칸이다. 즉, 이 욕실 바닥은 에반이 가진 타일로는 채울 수 없는 바닥이라는 뜻이 된다.
이 문제는 단순히 두 칸으로 이루어진 에반의 타일에 “검은색과 흰색이라는 주기성”을 부여하여 풀어나가는 문제이다. 에반의 타일이 가지고 있는 색의 주기와 욕실 바닥의 주기가 동일하지 않다면 그 욕실 바닥은 채울 수 없는 바닥이 되는 것이다.
그럼 검은색 칸을 -1, 흰색 칸을 1으로 정의하고, 욕실 바닥의 해당 칸을 만날 때마다 -1과 1을 번갈아가며 더한 후 마지막에 값이 0이 되면 검은색 칸과 흰색 칸의 수가 동일하다고 생각할 수 있겠다.
const floor = [
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 1, 1, 1, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 1, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 1, 1, 1, 1],
[0, 0, 0, 0, 1, 1, 1, 0],
];
const tile = [-1, 1];
let count = 0;
let tileIndex = 0;
floor.forEach((row, index) => {
tileIndex = Number(index % 2 === 0);
row.forEach(col => {
if (col === 1) {
count += tile[tileIndex];
}
tileIndex = tileIndex === 0 ? 1 : 0;
});
});
console.log(`검은 타일과 흰 타일의 개수 차이는 ${Math.abs(count)} 입니다.`);검은 타일과 흰 타일의 개수 차이는 2 입니다.각 row를 순회할 때 tileIndex를 다시 교정해주는 이유는, 이 행렬의 컬럼의 개수가 짝수이기 때문이다. 타일의 주기 또한 짝수이기에 다음 줄에서는 이전 줄의 가장 마지막에 있던 타일의 색이 다시 한번 나오게 된다. (컬럼을 홀수로 만들면 이 과정이 필요없는데, 문제 잘못 만들었다…)
문제만 보면 전혀 주기성과 관련이 없어보이는 문제였지만, 이렇게 문제 내에서 반복되는 패턴을 찾아내고 주기성을 부여함으로써 조금 더 간단한 방법으로 문제를 해결할 수 있다.
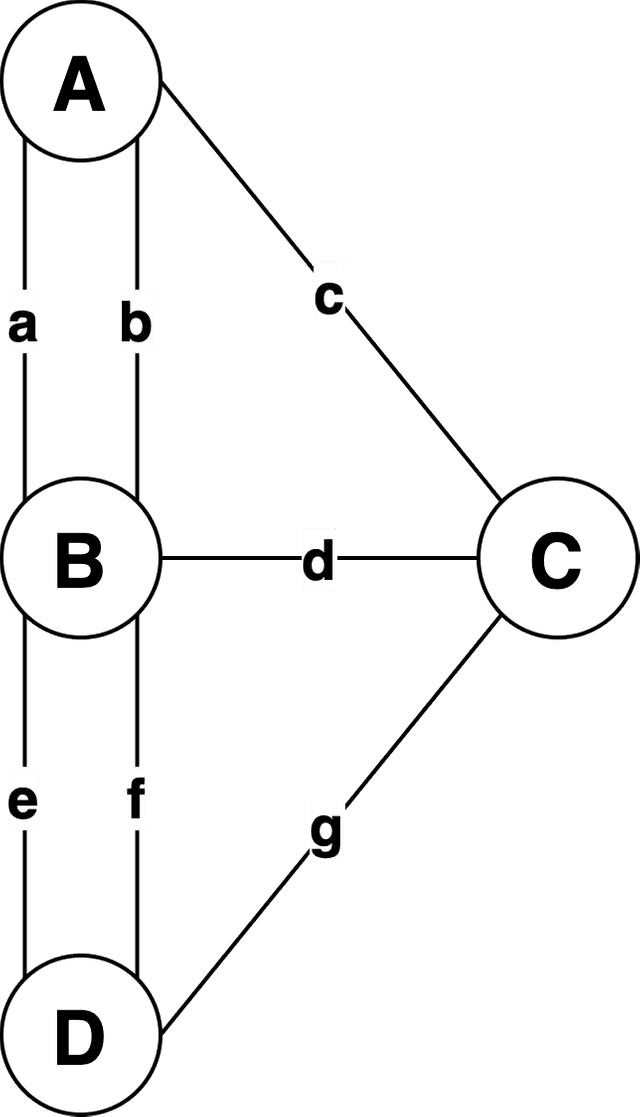
한 붓 그리기, 쾨니히스베르크의 다리 증명하기
쾨니히스베르크의 다리는 현대 위상 수학의 시작을 이끌었던 굉장히 유명한 문제로, 프로이센의 쾨니히스베르크(현재 러시아 칼리닌그라드)라는 도시에 있는 다리를 사용한 문제이다.
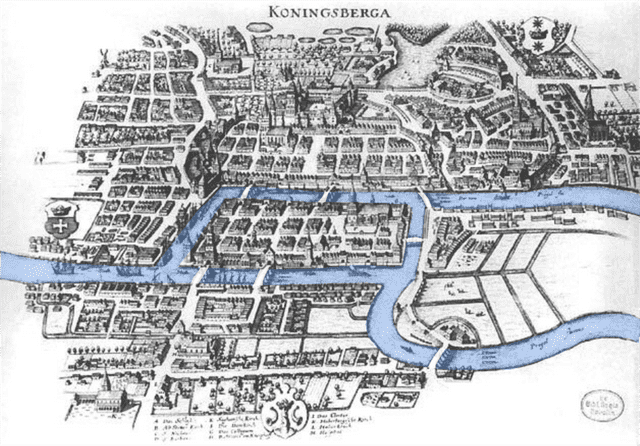
쾨니히스베르크의 한 가운데에는 프레골라 강이 흐르고 있고, 여기에는 가운데의 섬들과 연결되어있는 7개의 다리가 있다.
임의의 지점에서 출발하여 이 다리들을 한 번씩만 건너서 모든 다리를 건널 수 있을까?
즉, 한 붓 그리기 문제인 것이다. 이 문제를 그대로 보면 생각하기가 어려우니, 조금 더 그림을 단순하게 그리고 각 지역에 식별자를 부여한 후, 문제의 조건들을 정리해보도록 하자.
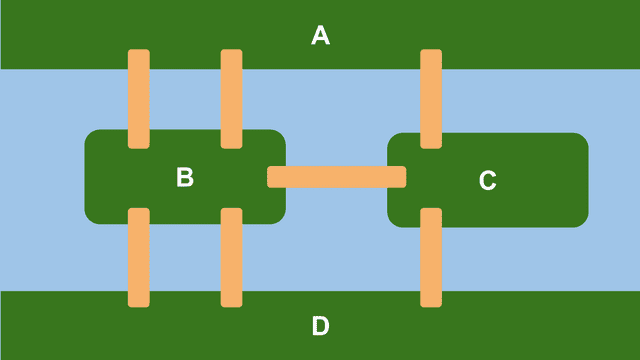
- 임의의 지점에서 출발할 수 있다.
- 모든 다리를 건너야 한다.
- 한번 건넌 다리는 다시 건널 수 없다.
- 각 구역은 몇 번을 들리든 상관없다.
- 출발한 구역으로 다시 돌아와도 되고 안 돌아와도 상관없다.
사실 몇 번 펜으로 쭉쭉 그어보면 대충 불가능하다는 감이 온다. 하지만 “절대로 건널 수 없다”라는 결론을 내리기 위해서는 왜 불가능하다는 것인지 증명하는 과정이 필요하다. 혹시 방법이 있는데 단순히 못 찾을 것일수도 있으니 말이다.
우선 이 문제를 조금 더 쉽게 생각해보기 위해 복잡한 지도 모양의 그림이 아닌, 단순화된 그래프로 다시 그려보도록 하겠다.
이때 그래프 내에서 A, B, C, D 구역의 역할을 하는 점을 정점(Vertex)이라고 하고, a - g 다리의 역할을 하는 선을 간선(edge)라고 하며, 각 정점에 붙어있는 간선의 개수를 차수(Degree)라고 한다.
쾨니히스베르크의 문제에서 다리를 건넌다는 것은 어떤 한 정점에서 다른 정점으로 넘어가는 것을 의미하며, 한번 건넌 다리는 다시 건널 수 없다는 것은 다른 정점으로 넘어갈 때 사용한 간선을 삭제해야한다는 것을 의미한다.
다리를 건너 이동할 수 있는 케이스를 한번 쭉 살펴보면 대략 처음 출발할 때, 마지막 도착할 때, 통과할 때의 3가지 케이스로 분류해볼 수 있는데, 이 3가지 케이스에서 간선이 삭제되는 개수에는 패턴이 숨어있다.
처음 출발할 때

어느 정점에서 출발하던 다른 정점으로 이동하는 경우는 출구 역할을 하는 간선만 삭제될 것이다. 즉, 출발 정점의 차수가 1 줄어든다.
마지막 도착할 때

출발할 때와는 반대로, 도착하는 정점은 입구의 역할을 했던 간선만 삭제하면 되므로, 해당 정점의 차수는 1 줄어든다.
통과할 때
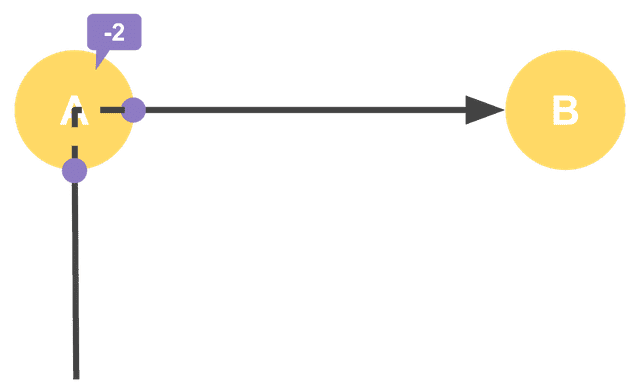
통과할 때는 입구의 역할을 하는 간선과 출구의 역할을 하는 간선을 삭제해야하므로, 해당 정점의 차수가 2씩 줄어든다.
즉, 어떤 그래프에서 한 붓 그리기가 성공했다는 것은 정점을 순회하다가 더 이상 건널 수 있는 간선이 없어졌을 때, 반드시 “모든 정점의 차수가 0이어야 한다는 것”이다. 만약 차수가 0이 아닌 정점이 존재한다면 그 정점에는 아직 건너지 않았던 간선이 연결되어 있다는 말이 되므로 한 붓 그리기는 실패한 것이 된다.
이때 우리는 각 정점의 차수가 1이나 2 씩 줄어들고 있다는 점에서 이 문제를 풀 수 있는 힌트를 얻을 수 있다.
차수의 홀짝 여부에 집중하자
차수가 1씩 줄어드는 경우는 한번 수행될 때마다 차수의 홀짝 여부가 변경되고, 2씩 줄어드는 경우는 차수의 홀짝 여부가 절대 변하지 않는다.
정점 차수의 홀짝 여부를 이야기하고 있는 이유는 바로 “0이 짝수이기 때문”이다.
즉, 정점에서 출발, 도착, 통과 시 변하는 차수의 홀짝 패턴을 파악하면 모든 경우의 수를 그려보지 않더라도 간단하게 이 그래프가 한 붓 그리기가 가능한 그래프인지 아닌지 알 수 있다.
출발지와 도착지가 같은 경우
우선 위에서 살펴본 바와 같이 중간에 통과하는 정점의 차수는 무조건 2씩 줄어들기 때문에 몇 번을 통과하든 차수의 홀짝 여부가 절대 변하지 않는다.
즉, 어떤 방식으로 건너든 통과 정점의 차수가 0이 되려면, 해당 정점의 차수는 처음부터 짝수여야한다는 것이다.
만약 통과 정점의 차수가 홀수라면 반드시 마지막에는 차수가 1이 되고, 이 간선을 타고 해당 정점에 도착하게되면 더 이상 남아있는 간선이 없기 때문에 다른 정점으로 건너갈 수 없게 된다.
 차수가 홀수인 통과 정점에 들어서면 맘대로 나갈 수 없다
차수가 홀수인 통과 정점에 들어서면 맘대로 나갈 수 없다
또한 출발지와 목적지가 같은 경우에는 맨 처음 출발할 때 출발 정점의 차수를 1 줄이고 도착할 때 다시 1을 줄여야하기 때문에, 최종적으로는 해당 정점의 차수가 총 2만큼 줄어들게 된다.
이 경우에도 출발 정점의 차수는 홀짝 여부가 변경될 수 없기 때문에 반드시 처음부터 짝수인 차수를 가지고 있어야 한다는 말이 된다. 즉, 출발지와 도착지가 같은 경우 한 붓 그리기가 성공하려면 “모든 정점의 차수가 짝수여야 한다는 결론”이 나온다.
출발지와 도착지가 다른 경우
출발지와 도착지가 다른 경우에도 통과 정점의 차수는 처음부터 짝수여야 한다는 점은 달라지지 않지만, 이번에는 출발지와 도착지가 다르기 때문에 출발 정점과 도착 정점의 차수는 반드시 홀수여야 한다는 점이 다르다.
중간에 통과하는 정점은 반드시 차수가 2씩 줄어들기 때문에 홀짝이 변하지 않지만, 출발과 도착 시에는 차수가 1만 줄어들기 때문에 홀짝 여부가 변하기 때문이다.
즉, 출발지와 도착지가 다른 경우는 “출발지와 도착지는 홀수 차수, 그 외 정점은 짝수여야한다”라는 결론이 나온다.
쾨니히스베르크의 다리는 왜 한 붓 그리기가 불가능할까?
이 두 가지 조건을 정리해보자면 그래프의 정점을 순회하며 한 붓 그리기가 가능한 경우는 “모든 정점이 짝수 차수를 가지고 있거나 홀수 차수가 2개인 경우”라고 정리해볼 수 있다. 다시 쾨니히스베르크의 다리를 도식화한 그래프를 살펴보고 이 조건에 맞아떨어지는지 확인해보자.
이 그래프의 정점들의 차수를 정리해보면 A=3, B=5, C=3, D=3으로 모든 정점의 차수가 홀수이므로, 위에서 찾아낸 어떤 조건과도 맞지 않는다.
즉, 쾨니히스베르크의 다리는 한 붓 그리기가 불가능한 구조라는 것이 증명된 것이다.
그래프 이론에서 이렇게 한 붓 그리기, 즉, 그래프의 모든 경로를 단 한 번씩만 통과하는 경로를 오일러 경로(Eulerian Trail)라고 부르는데, 그 이유는 갓 레온하르트 오일러 형님이 이미 1735년에 이 문제를 증명하고 자기 논문에 써먹었기 때문이다.
해당 논문은 Solutio Problematis ad Geometriam Situs Pertinentis에서 확인할 수 있지만, 제목에서도 느껴지듯이 이게 영어가 아니다. 이 시대의 가방끈 기신 분들이 작성한 논문이 다들 그러하듯 라틴어로 작성되어있기 때문에 읽어보는 건 사실 힘들다. 그래도 혹시 필자의 상상을 뛰어넘어 라틴어가 가능하신 굇수분들이 있을 수 있으니 일단 첨부하겠다.
어쨌든 오일러 형님의 문제 풀이에서 주목해야하는 아이디어는 각 정점의 차수를 조사할 때 차수 자체가 아닌 홀수와 짝수라는 성질에 주목했다는 점이다. 정점에서 출발할 때, 도착할 때, 통과할 때 정점이 가진 차수의 상태가 홀짝으로 변화하는 그 패턴을 파악하지 못했다면 이 문제를 해결하기는 힘들었을 것이다.
마치며
이번 포스팅에서 살펴본 3개의 문제는 어려운 수학 공식을 사용하는 문제가 아니다.
7일마다 반복되는 패턴에서 착안하여 일 후의 요일도 뭔가 패턴이 있을 것이라는 추론, 두 칸짜리 타일을 보고 검은색과 흰색이 반복되는 패턴을 떠올릴 수 있는 것, 그래프 순회의 모든 경우의 수를 따져보지 않고 각 정점의 차수가 홀짝으로 변화하는 패턴을 생각해낼 수 있는 것 등은 복잡한 수학 공식을 모르더라도 수의 성질만 알고 있다면 누구든지 접근할 수 있는 문제 해결 방식이다.
이렇게 수의 근본적인 성질을 파악하고 이용하면 복잡한 문제를 단순하게 풀 수 있다. 슬픈 점은 이게 단순히 공부로 얻어질 수 있는 능력이 아니라는 것이다. 이런 능력을 키우기 위해서는, 그냥 이렇게 생각하는 연습을 많이 해야하는 것 같다.
코딩 테스트를 많이 풀어보는 것도 물론 좋지만, 일상 속에서 겪는 다양한 문제들 속에서 이렇게 패턴을 찾아내고 분석해보는 것도 나름 도움이 되지 않을까? 예를 들면 친구가 11월 10일에 약속을 잡자고 했는데, 그때가 무슨 요일인지 핸드폰으로 확인하는 것이 아니라 한번 직접 계산해본다던가 하는 식으로 말이다.
이상으로 수학과 함께 복잡한 문제를 단순하게 만들자! 포스팅을 마친다.