Building a Simple Artificial Neural Network with TypeScript

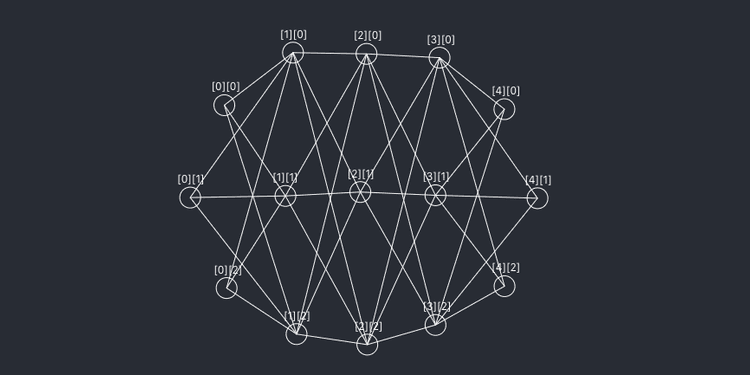
In this post, following the previous post, I want to briefly organize what I built - a simple artificial neural network using TypeScript.

I wrote this application for a Tech seminar presentation at my current workplace, so development time was quite tight. Therefore, I couldn’t implement all the features I had in mind and plan to add more features later.

Since I had experience writing a completely hardcoded ANN using JavaScript before, I thought about recycling that code.

But when I actually tore it apart, there weren’t really any parts I could recycle, so I just decided to write it from scratch again. Before entering development, the design and features I abstractly envisioned were as follows:

1. No more hardcoding! Let’s do structural design.
2. The number of layers and nodes per layer should be freely changeable.
3. It would be nice to visualize the process of loss decreasing and changes in weights!
4. Let’s enable changing application inputs and initial weight values directly within the application!

Among these, I couldn’t do #4 due to time shortage since I had to make seminar PPT too, but I somehow succeeded in implementing #1-3 within time.

Loss Varies Depending on Neuron Connections

First, I had to think about how to implement the feature of updating weights, which is ANN’s core function. Actually, when proceeding with forward propagation, most values needed during backpropagation can be pre-calculated. First, I’m going to proceed with explanation by bringing the example I used in the previous post.

First, the formula for updating weights in backpropagation is as follows:

1. $\frac{\partial E}{\partial a}$: Contribution of neuron’s output ($a$) affecting error ($E$)

2. $\frac{\partial a}{\partial z}$: Contribution of input ($x$) and weight ($w$) product ($z$) affecting neuron’s output ($a$)

3. $\frac{\partial z}{\partial w}$: Contribution of weight ($w$) affecting input x weight ($z$)

Actually, when updating a neuron’s weight, formulas #2 and #3 don’t change. What changes is only #1, the contribution of the neuron’s output affecting error. More precisely, only the method of calculating contribution changes depending on situation. Let’s look at the following 2 cases.

When Neuron’s Output Affects Only a Specific Error

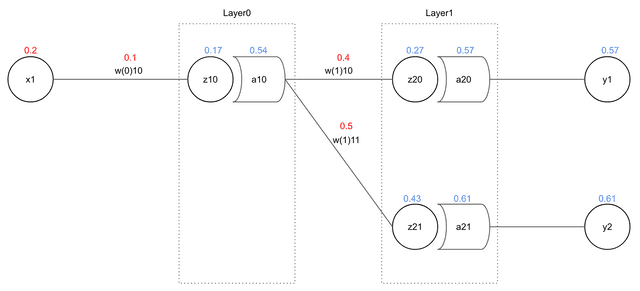
Assuming we calculate final error as MSE (Mean Squared Error) in this network, error can be represented as follows:

As you can see in the above formula, while $a_{20}$ can affect $E_1$, it absolutely cannot affect $E_2$. That variable itself isn’t in the formula at all. Therefore, when calculating $\frac{\partial E}{\partial a_{20}}$, we can completely consider all errors except $E_1$ as 0 and calculate.

When Neuron’s Output Affects Multiple Errors

Let’s look at layers once more. This time we need to find out how much $a_{10}$, which is more inside, affected total error $E$.

Just looking at the connected lines, you can see this guy is spreading legs everywhere. Not only neurons that used $a_{10}$ as input, but neurons that used output sent by these neurons and many things must have been affected. So this time we can’t do things like ignoring other variables like before. We need to calculate everything.

Here, $\frac{\partial E}{\partial a_{10}}$ means error propagated from the last layer to just behind the layer where the neuron that sent out a_10 as output belongs.

And $\frac{\partial E_1}{\partial a_{10}}$ and $\frac{\partial E_2}{\partial a_{10}}$ that compose this error are obtained like this:

Since $\frac{\partial E_1}{\partial a_{20}}$ and $\frac{\partial E_2}{\partial a_{21}}$ that appeared in this formula are the same case as #1 seen above, calculating like #1 should work. There was one part I was confused about when implementing this formula in code.

Let’s look at the formula obtaining $\frac{\partial E_1}{\partial a_{10}}$. There are 2 variables the neuron doesn’t have.

1. $E_1$: Loss propagated from rear layer
2. $a_{10}$: Output of front layer neuron

So at first I thought

What, do I need to access both front and back layers when iterating to get them? Need to do exception handling twice too, annoying…

But…

Yeah, thinking about it, this value was just the input this neuron receives.

It was an awesome fact I was missing because I kept focusing only on variables. After 3 seconds of silence for my lacking brain, I moved to the next step.

Writing Pseudocode

After thinking up to here, I first wrote brief pseudocode. Originally I wrote it scribbling in a notebook, but here I’ll write it in TypeScript syntax for Syntax Highlighting.

I envisioned 3 basic classes total: Network, Layer, Neuron. I thought a lot about how to implement just forward propagation and backpropagation, so I only wrote pseudocode related to backpropagation.

Neuron

In the Neuron class, when backpropagation proceeds, it should update weights the Neuron object has, and at this time use $\frac{\partial a}{\partial z}$ pre-calculated during forward propagation to also calculate $\frac{\partial E}{\partial a}$, the contribution of the neuron’s output affecting propagated error.

class Neuron {
  private activationFunction미분값: number;
  private weights: number[]; // Neuron's weights
  private weight미분값들: number[]; // Contributions of neuron's inputs affecting total error

  public weight들업데이트 (에러미분꼴: number, 학습속도: number) {
    const 새로운weight들 = this.weights.map((weight, index) => {

      // Obtain contribution of wx value affecting error
      const loss = 에러미분꼴 * this.activationFunction미분꼴;

      // weight is the same as contribution of x affecting wx value.
      // Multiplying with loss gives contribution of x affecting error.
      this.weight미분값들[index] = loss * weight;

      // x is the same as contribution of weight affecting wx value.
      // Multiplying with loss gives contribution of w affecting error.
      return weight - (학습속도 * (loss * this.inputs[index]));
    });

    this.weights = 새로운weight들;
  }
}

Layer

The Layer class runs iterations during backpropagation and calls methods of neurons it has.

At this time, if it’s the last layer, it uses MSE’s derivative $-(target_i - output_i)$. If not the last layer, when updating the weights array of neurons in the next layer, it takes necessary elements from the pre-calculated weights미분값들 array, adds them all, then passes them to neurons in the current layer.

class Layer {
  public 다음레이어: Layer;
  private 뉴런들: Neuron[];

  public 뉴런들업데이트 (전파된에러들: any[], 학습속도: number) {
    if (다음레이어) {
      // Since it's not the last layer, among passed errors
      // must specify index of weight calculated together with this neuron's output.
      this.뉴런들.forEach((뉴런, index: number ) => {
        const loss = 전파된에러들.reduce((a: number, b: number[]) => a +_b[index], 0);
        neuron.updateWeights(loss, 학습속도);
      });
    }
    else {
      // If last layer, only need to pass contribution to error each neuron affected.
      this.뉴런들.forEach((뉴런, index: number) => {
        neuron.updateWeights(loss[index], 학습속도);
      });
    }
  }
}

Looking at the method, if the layer to currently update isn’t the last layer, error’s data type changes from number[] to number[][]. The reason is because having the index value weights have inside neurons makes calculation convenient.

[[wp_0_0, wp_0_1, wp_0_2], [wp_1_0, wp_1_1, wp_1_2]]

The next layer’s error is returned in this 2D array form. At this time, if trying to update weights of the neuron at index 0 of the layer, we must extract only errors connected with this neuron from the next layer’s errors.

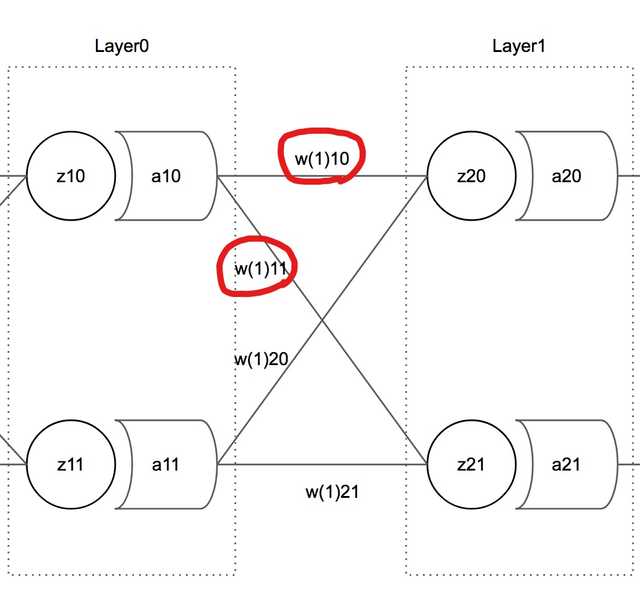
As shown in this picture, weight variables calculated together with $a_{10}$ are stored as the 0th element of the weights array of neurons in the next layer.

In other words, if the index of the neuron to update is 0, we can say it only affected all Neuron.weights[0] in the next layer, and therefore the error to reference is also Neuron.weightPrimes[0].

Network

The Network class has responsibilities like creating layers and neurons, controlling network operations like forward propagation or backpropagation, and managing integrated results or errors.

class Network {
  학습속도: number;
  레이어들: Layer[];
  인풋레이어: Layer;
  아웃풋레이어: Layer;
  전체에러미분값들: number[]; // -(target_i - output_i)s

  public backPropagation () {
    const 뒤집힌레이어들 = [...this.레이어들]reverse();
    const 학습속도 = this.학습속도;
    뒤집힌레이어들.forEach(레이어 => {
      let 에러들: any = [];

      if (레이어.id === this.아웃풋레이어.id) {
        에러들 = this.전체에러미분값들;
      }
      else {
        // Backpropagation is proceeding so next layer's calculation finished first.
        // Accessing private member variables causes errors but it's pseudocode so let's pass
        에러들 = 레이어.다음레이어.뉴런들.map(뉴런 => 뉴런.weightPrimes);
      }
      레이어.뉴런들업데이트(에러들, 학습속도);
    });
  }
}

Wrapping Up

If written roughly like this, now just run iterations in the main function.

const network = new Network();

for (let i = 0; i < 학습횟수; i++) {
  network.forwardPropagation();
  network.backPropagation();
  console.log(network.getResults());
}

Well, doing it roughly like this should work. Forward propagation wasn’t difficult since you just calculate iteratively, but backpropagation was a bit hard at first because it didn’t come intuitively.

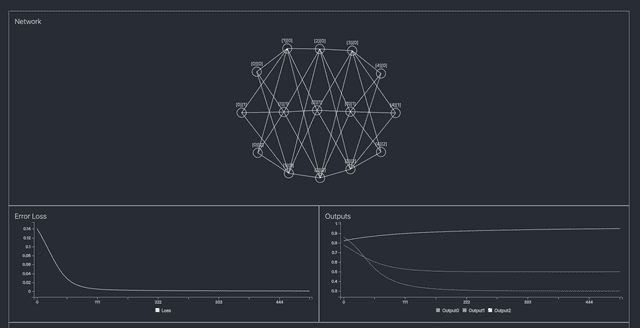Modestly completed appearance

Still, I somehow implemented the network in time for the seminar, and after doing modest visualization using D3, I felt proud. Next time when I have time, I want to improve it so activation functions can be changed per layer or loss functions can also be changed.

That’s all for this post on grunt work developing a simple artificial neural network using TypeScript. Full source can be checked in the GitHub repository and a live demo is available here.