[Deep Learning 시리즈] Backpropagation, 역전파 알아보기

이번 포스팅에서는 저번 포스팅에 이어 Backpropagation에 대해서 알아보려고 한다. 앞서 설명했듯, 이 알고리즘으로 인해 Multi Layer Network에서의 학습이 가능하다는 것이 알려져, 암흑기에 있던 Neural Network 학계가 다시 관심을 받게 되었다.

Backpropagation이란?

Backpropagation은 오늘 날 Artificial Neural Network를 학습시키기 위한 일반적인 알고리즘 중 하나이다. 한국말로 직역하면 역전파라는 뜻인데, 내가 뽑고자 하는 target값과 실제 모델이 계산한 output이 얼마나 차이가 나는지 구한 후 그 오차값을 다시 뒤로 전파해가면서 각 노드가 가지고 있는 변수들을 갱신하는 알고리즘인 것이다.

다행히 여기까지는 직관적으로 이해가 되지만 필자는 다음 2가지의 원리가 궁금했다.

1. 각 노드가 가지고 있는 weight이나 bias같은 변수들을 어떻게 업데이트할 것인가?
2. Multi Layer Network에서 각 노드나 레이어가 가지고 있는 변수들은 다 제 각각인데 그 값들을 얼만큼 변경하는 지 어떻게 알 수 있는가?

다행히 이 문제들은 Chain Rule이라는 법칙을 사용해 해결할 수 있다고 한다. 한번 차근차근 살펴보자.

Chain Rule이란?

Chain Rule, 미분의 연쇄법칙이라고도 불리는 법칙이다. 이건 고딩때는 안배우고 대학수학에서 배우기 때문에, 대학 때 이산수학만 배웠던 필자는 이해가 잘되지않아서 고생했다. 먼저 정의부터 보자.

함수 $f, g$가 있을 때

$f$와 $g$가 모두 미분 가능하고

$F = f(g(x)) = f \circ g$로 정의된 합성 함수이면 $F$는 미분 가능하다.

이때 $F'(x) = f'(g(x)) \centerdot g'(x)$이다.

$t = g(x)$라고 한다면,

$\frac{dy}{dx} = \frac{dt}{dx} \frac{dy}{dt}$가 성립한다.

정의를 보면 뭔 말인가 싶을 수 있는데, 먼저 합성함수는 그냥 어떤 함수의 인자로 다른 함수가 주어진 함수이다. 대충 이런 식이랄까?

function f(g) {
  return g * 3;
}
function g(x) {
  return x + 1;
}

const x = 3;
let F = f(g(x));
// F = 12

그럼 미분 가능하다라는 말이 의미하는 것은 뭘까? 보통 미분 = x와 x'간의 기울기를 구한다 정도로 이해하고 있다면 합성함수 어쩌고에서 기울기를 왜 구하지? 라고 생각할 수 있다.

하지만 기울기를 구한다라는 말은 변화량을 구한다라고도 할 수 있다. 위의 코드를 보면 변수 F를 선언할 때 g에 주는 값을 변경한다면 최종적으로 F값이 바뀐다는 것을 알 수 있을 것이다.

F = f(g(4));
// F = 15
F = f(g(2));
// F = 9

즉 Chain Rule이란 쉽게 얘기하자면 1. x가 변화했을 때 함수 g가 얼마나 변하는 지와 그로인해 2. 함수 g의 변화로 인해 함수 f가 얼마나 변하는 지를 알 수 있고 3. 함수 f의 인자가 함수 g이면 최종 값 F의 변화량에 기여하는 각 함수 f와 g의 기여도를 알 수 있다는 것이다.

방금 전 위에서 예시로 든 합성함수 F의 식에 들어가는 변수는 x 하나였다. 그럼 변수가 여러 개면 어떻게 되는 걸까?

이변수함수 $z = f(x, y)$에서 $x = h(s,t), y = g(s,t)$일 때

$f(x,y), g(s,t), h(s,t)$가 모두 미분 가능하면

로 나타내어질 수 있다.

이 말인 즉슨 $s$나 $t$가 얼만큼인지는 모르지만 어쨌든 변했을 때, 함수 $z$의 변화량을 저런 식으로 구할 수 있다는 것이다.

그리고 $\partial$는 편미분을 뜻하는 기호인데, 메인이 되는 변수 하나를 남겨두고 나머지 변수는 그냥 개무시하는 미분법이다. 그래서 $s$와 $z$의 관계를 구하는 식에서는 아예 $t$가 없는 것을 알 수 있다.

여기까지 이해가 되었다면 이제 본격적으로 Backpropagation이 어떻게 진행되는 지 살펴보도록 하자.

Forward-propagation

이제 직접 Backpropagation이 어떻게 이루어지는 지 한번 계산해보자.

그 전에 먼저 Forward Propagation을 진행해야한다. 초기화한 $w$값과 input인 $x$을 가지고 계산을 진행한 뒤 우리가 원하는 값이 나오는 지, 나오지 않았다면 얼마나 차이가 나는지를 먼저 구해야한다.

필자가 이번 계산에 사용할 모델은 아래와 같다.

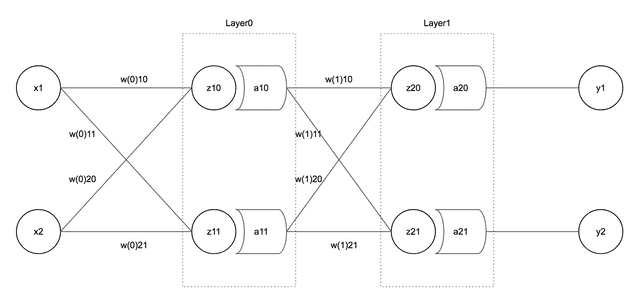
이 모델은 2개의 input, 2개의 output을 가지고 2개의 Hidden Layer를 가진 2-Layer NN 모델이다. 이제 각 변수에 값을 할당해보자.

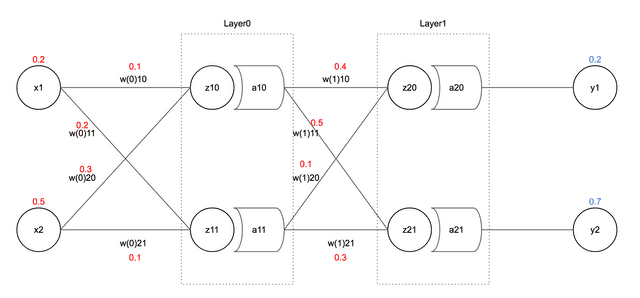
먼저 필자가 output으로 원하는 $y_1$의 값은 0.2, $y_2$의 값은 0.7이다. 그리고 input으로는 $x_1$에 0.2, $x_2$에 0.5를 넣어주었고, 각각의 $w$값은 그냥 느낌 가는대로 넣어놓았다.

필자는 이 계산에서 Activation Function으로 Sigmoid함수를 사용하고, Error Function은 Mean Squared Error함수를 사용하려고 한다.

먼저 Layer0에서 받을 값부터 계산해보자. 보통 행렬로 계산한다.

저 행렬 곱을 풀어보면 다음과 같이 되고 결국 $wx$들의 합의 형태로 나타난다.

$z_{10}$와 $z_{11}$의 값을 구했으면 이제 Activation Function을 사용하여 $a_{10}$와 $a_{11}$값을 구해보자. 필자가 사용할 Activation Function인 Sigmoid의 수식은 다음과 같다.

이걸 매번 손으로 계산하면 너무 번거롭기 때문에 JavaScript를 사용해 다음과 같이 함수를 하나 만들어 놓고 사용했다.

function sigmoid(x) {
  return 1 / (1 + Math.exp(-x));
}

다음 레이어도 같은 방식으로 값을 계속 구해보면 다음과 같은 값들을 구할 수 있다.

결국 $y_1$와 $y_2$는 각각 $a_{20}$과 $a_{21}$과 같으므로, 우리는 최종 output값을 구하게 되었다. 근데 우리가 처음에 원했던 $y_1$과 $y_2$는 0.2와 0.7이었는데, 우리가 구한 output은 0.57과 0.61으로 거리가 있다.

이제 Mean Squared Error함수를 사용하여 에러 $E$를 구할 차례이다. 결과값으로 얻기를 바라는 값을 $t$로, 실제 나온 값을 $y$라고 할 때 에러 $E$는 다음과 같다.

필자같은 수포자를 위해 쉽게 설명하자면, 그냥 마지막 Output Layer에서 뱉어낸 $y$들과 하나하나 레이블링했던 $\hat{y}$가 얼마나 차이나는 지 구한 다음에 그 값들의 평균을 내는 것이다.

결국 ANN을 학습시킨다는 것은 이렇게 구한 에러 $E$의 값을 0에 근사시킨다고 볼 수 있다. 여기서 나온 $E$값을 이제 Backpropagation하면 되는 것이다.

이것도 매번 손으로 계산하기 귀찮으니까 그냥 함수를 하나 만들자.

function MSE(targets, values) {
  if (values instanceof Array === false) {
    return false;
  }

  let result = 0;
  targets.forEach((target, i) => {
    result += 0.5 * (target - values[i]) ** 2;
  });

  return result;
}

MSE([0.2, 0.7], [0.57, 0.61]); // 0.072

이제 여기서 구한 에러 $E$값을 사용하여 Backpropagation을 진행해보자.

Backpropagation

Frontend Propagation을 통해서 구해진 값을 다시 그림으로 살펴보면 다음과 같다.

필자는 이 중 현재 0.4로 할당되어 있는 $w^1_{10}$값을 업데이트 하려고 한다. 그러려면 $w^1_{10}$이 전체 에러인 $E$에 얼마나 영향을 미쳤는지, 즉 기여도를 구해야한다. 이때 위에서 설명한 Chain Rule이 사용된다.

$E$에 대한 $w^1_{10}$의 기여도를 식으로 풀어보면 다음과 같다.

먼저 $\frac{\partial E}{\partial a_{20}}$부터 차례대로 풀어보자. 원래 우리가 구한 $E$는 아래와 같은 식이였다.

여기서 $a_{20} = y_1, a_{21} = y_2$이기 때문에 치환해주었다. 하지만 $\frac{\partial E}{\partial a_{20}}$는 편미분식이기 때문에 지금 구하려는 값과 상관없는 $a_{21}$는 그냥 0으로 생각하고 풀면된다.

이 계산 결과가 의미하는 것은 전체 에러 $E$에 대하여 $a_{20}$, 즉 $y_1$가 0.37만큼 기여했다는 것을 의미한다. 이런 식으로 계속 계산해보자.

최종적으로 $E$에 $w^1_{10}$가 기여한 값은 0.049이라는 값을 계산했다. 이제 이 값을 학습식에 넣으면 $w^1_{10}$값을 업데이트 할 수 있다.

이때 값을 얼마나 건너뛸 것이냐 또는 얼마나 빨리 학습시킬 것이냐 등을 정하는 Learning Rate라는 값이 필요한데, 이건 그냥 사람이 정하는 상수이고 보통 0.1보다 낮은 값으로 설정하나 필자는 0.3으로 잡았다.

이렇게 해서 필자는 새로운 $w^1_{10}$값인 0.3853을 얻었다. 이런 식으로 다른 $w$값을 계속 업데이트 해보자. 이번에는 Layer1보다 한 층 더 깊숙히 있는 Layer0의 $w^0{10}$값을 업데이트 할 것이다.

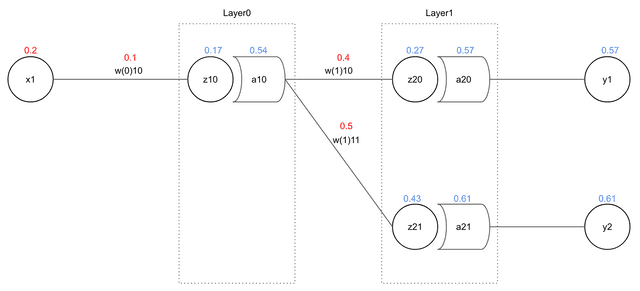
보다시피 $w^0_{10}$은 $w^1_{10}$보다 많은 값에 영향을 미치고 있다. 전체 에러 $E_t$에 $w^0_{10}$가 기여한 정도는 다음과 같이 나타낼 수 있다.

그럼 먼저 $\frac{\partial E_1}{\partial a_{10}}$부터 구해보자.

마찬가지로 $\frac{\partial E_2}{\partial a_{10}}$도 구해본다.

이제 $\frac{\partial E_1}{\partial a_{10}}$와 $\frac{\partial E_2}{\partial a_{10}}$를 전부 구했으니 $\frac{\partial E_t}{\partial w^0_{10}}$를 구할 차례이다.

이로써 $w^0_{10}$이 전체 에러 $E_t$에 0.0034만큼 기여한다는 걸 알아냈다. 이제 이 값을 사용하여 $w^0_{10}$값을 업데이트하자. Learning Rate는 아까와 동일한 0.3이다.

코딩하기

필자는 도저히 이걸 8번이나 손으로 풀 수 있는 사람이 아니기 때문에 JavaScript를 사용하여 위에 설명했던 공식을 간단하게 코드로 작성해보았다.

function sigmoid(x) {
  return 1 / (1 + Math.exp(-x));
}

function MSE(targets, values) {
  if (values instanceof Array === false) {
    return false;
  }

  let result = 0;
  targets.forEach((target, i) => {
    result += 0.5 * (target - values[i]) ** 2;
  });

  return result;
}

// 인풋 초기화
const x1 = 0.2;
const x2 = 0.5;

// 타겟 값 초기화
const t1 = 0.2;
const t2 = 0.7;

// Weights 초기화
const w0 = [
  [0.1, 0.2],
  [0.3, 0.1],
];
const w1 = [
  [0.4, 0.5],
  [0.1, 0.3],
];
const learningRate = 0.3;
const limit = 1000; // 학습 횟수

// 두번째 Layer의 Weight들을 업데이트
function updateSecondLayerWeight(targetY, y, prevY, updatedWeight) {
  const v1 = -(targetY - y) + 0;
  const v2 = y * (1 - y);
  const def = v1 * v2 * prevY;
  return updatedWeight - learningRate * def;
}

// 첫번째 Layer의 Weight들을 업데이트
function updateFirstLayerWeight(t1, t2, y1, y2, w1, w2, a, updatedWeight) {
  const e1 = -(t1 - y1) * y1 * (1 - y1) * w1;
  const e2 = -(t2 - y2) * y2 * (1 - y2) * w2;
  const v1 = a * (1 - a);
  const v2 = a;
  const def = (e1 + e2) * v1 * v2;

  return updatedWeight - learningRate * def;
}

// 학습 시작
let i = 0;
for (i; i < limit; i++) {
  let z10 = x1 * w0[0][0] + x2 * w0[1][0];
  let a10 = sigmoid(z10);
  let z11 = x1 * w0[0][1] + x2 * w0[1][1];
  let a11 = sigmoid(z11);

  let z20 = a10 * w1[0][0] + a11 * w1[1][0];
  let a20 = sigmoid(z20);
  let z21 = a10 * w1[0][1] + a11 * w1[1][1];
  let a21 = sigmoid(z21);

  let e_t = MSE([t1, t2], [a20, a21]);

  console.log(`[${i}] y1 = ${a20}, y2 = ${a21}, E = ${e_t}`);

  // 계산된 기여도들을 사용하여 새로운 Weight로 업데이트
  const newW0 = [
    [
      updateFirstLayerWeight(t1, t2, a20, a21, w1[0][0], w1[0][1], a10, w0[0][0]),
      updateFirstLayerWeight(t1, t2, a20, a21, w1[1][0], w1[1][1], a11, w0[0][1]),
    ],
    [
      updateFirstLayerWeight(t1, t2, a20, a21, w1[0][0], w1[0][1], a10, w0[1][0]),
      updateFirstLayerWeight(t1, t2, a20, a21, w1[1][0], w1[1][1], a11, w0[1][1]),
    ],
  ];
  const newW1 = [
    [updateSecondLayerWeight(t1, a20, a10, w1[0][0]), updateSecondLayerWeight(t2, a21, a10, w1[0][1])],
    [updateSecondLayerWeight(t1, a20, a11, w1[1][0]), updateSecondLayerWeight(t2, a21, a11, w1[1][1])],
  ];

  // 업데이트된 Weight들을 반영한다
  newW0.forEach((v, i) => {
    v.forEach((vv, ii) => (w0[i][ii] = vv));
  });
  newW1.forEach((v, i) => {
    v.forEach((vv, ii) => (w1[i][ii] = vv));
  });
}

console.log(`t1 = ${t1}, t2 = ${t2}`);

계산된 결과들을 보면 처음에 Multi Layer Network에 넣었던 x1과 x2가 점점 t1과 t2로 수렴하는 것을 볼 수 있다. 1000번 돌린 결과를 전부 볼 수는 없으니까 처음과 중간, 마지막 진행 상황을 첨부한다.

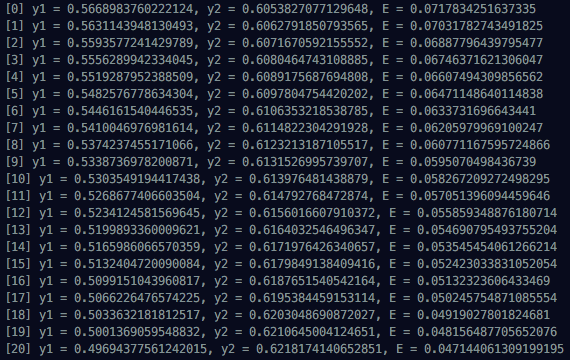
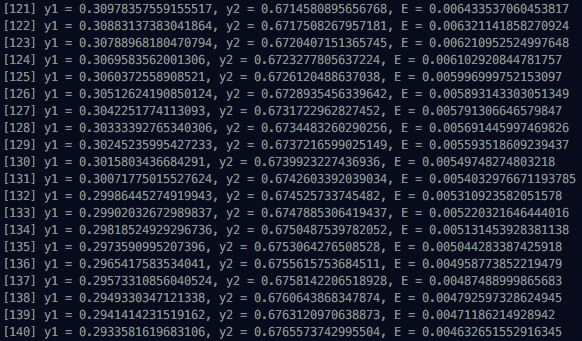
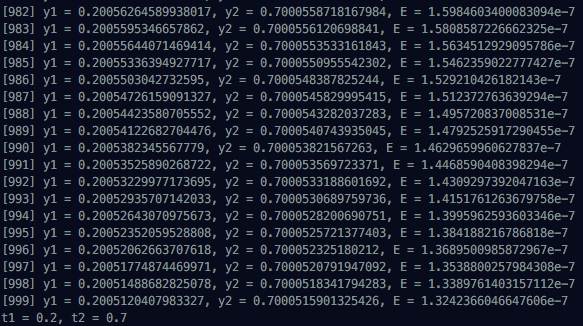
다음 포스팅에서는 좀 더 구조화한 네트워크를 만들어보려고 한다. 이상으로 Backpropagation 포스팅을 마친다.

• Backpropagation이란?
• Chain Rule이란?
• Forward-propagation
• Backpropagation
• 코딩하기