TypeScript와 함께 간단한 인공 신경망 만들기

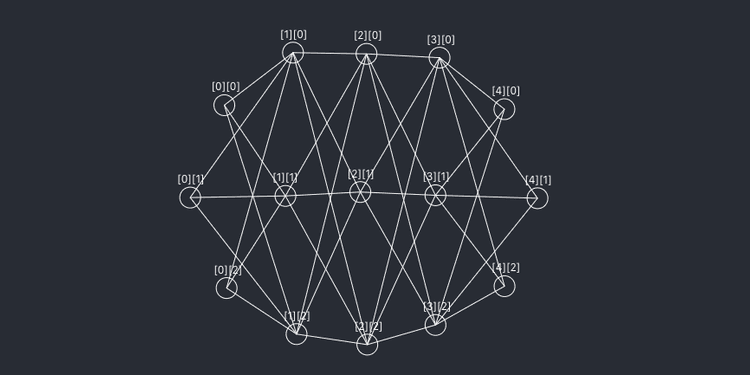
이번 포스팅에서는 저번 포스팅에 이어 TypeScript를 사용하여 간단한 인공신경망을 만들어본 것을 간단하게 정리하려고 한다.

이 어플리케이션은 현 직장에서 진행하는 Tech 세미나의 발표용으로 작성한 것이기 때문에 상당히 개발 시간이 촉박했다. 그래서 머릿속으로 생각해놓았던 기능을 전부 구현하지는 못했고 추후 기능을 더 추가해볼 예정이다.

예전에 JavaScript를 사용하여 완전 하드코딩한 ANN을 작성해본 경험이 있었기 때문에 그 코드를 재활용해볼까 생각했었다.

근데 막상 뜯어보니까 재활용할 수 있는 부분이 딱히 없어서 그냥 처음부터 다시 짜기로 했다. 개발에 들어가기에 앞서서 그냥 추상적으로 생각했던 설계와 기능은 이러했다.

1. 하드코딩은 그만! 구조적인 설계를 하자.
2. 레이어 개수, 한 레이어당 노드 개수는 자유자재로 변할 수 있어야 한다.
3. Loss가 줄어드는 과정이나 Weight들의 변화를 시각화해서 보면 좋을 것 같다!
4. 어플리케이션 인풋이나 초기 Weight 값을 어플리케이션 내에서 직접 변경할 수 있도록 하자!

이중 4번은 세미나 PPT도 만들어야 하므로 결국 시간 부족으로 하지 못했고, 1-3번까지는 어떻게든 시간 내에 구현에 성공했다.

뉴런의 연결에 따라 달라지는 Loss

일단 처음에는 ANN의 핵심 기능인 Weight를 업데이트하는 기능을 어떻게 구현할 것인가를 고민해야했다. 사실 Forward propagation을 진행할 때에 Backpropagation 때 필요한 대부분의 값을 미리 계산해놓을 수 있다. 우선 저번 포스팅에서 사용했던 예시를 가져와서 설명을 진행하려고 한다.

먼저 Backpropagation에서 Weight를 업데이트하는 공식은 다음과 같다.

1. $\frac{\partial E}{\partial a}$: 뉴런의 아웃풋($a$)이 에러($E$)에 영향을 끼친 기여도

2. $\frac{\partial a}{\partial z}$: 인풋($x$)과 Weight($w$)의 곱($z$)이 뉴런의 아웃풋($a$)에 영향을 끼친 기여도

3. $\frac{\partial z}{\partial w}$: Weight($w$)가 인풋 x Weight($z$)에 영향을 끼친 기여도

사실 뉴런의 Weight를 업데이트할 때 2번과 3번의 식은 변하지 않는다. 변하는 것은 오직 1번, 뉴런의 아웃풋이 에러에 영향을 끼친 기여도 뿐이다. 더 정확히 말하면 상황에 따라 기여도를 계산하는 방법만 바뀐다. 다음 2가지 케이스를 살펴보자.

뉴런의 아웃풋이 특정 에러에만 영향을 끼친 경우

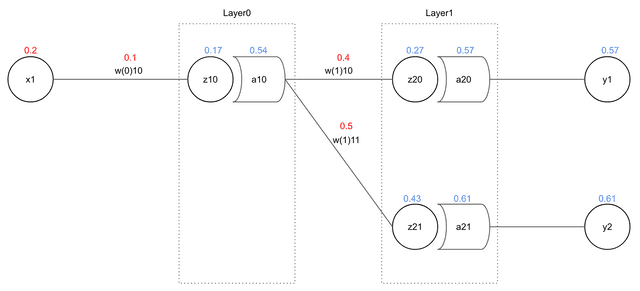
이 네트워크에서 최종 에러를 MSE(Mean Sqaured Error)로 구한다고 가정했을 때 에러는 다음과 같이 나타낼 수 있다.

위 식에서도 볼 수 있듯이 $a_{20}$의 경우 $E_1$에는 영향을 끼칠 수 있지만 절대 $E_2$에는 영향을 끼칠 수 없다. 아예 식에 그 변수 자체가 없다. 그렇기 때문에 우리는 $\frac{\partial E}{\partial a_{20}}$을 계산할 때 아예 $E_1$을 제외한 나머지 에러를 모두 0으로 간주하고 계산할 수 있다.

뉴런의 아웃풋이 여러 에러에 영향을 끼친 경우

다시 한번 레이어를 보자. 이번에는 좀 더 안쪽에 있는 $a_{10}$이 전체 에러 $E$에 얼마나 영향을 끼쳤는지 알아내야한다.

그냥 이어져 있는 선만 봐도 이 놈은 여기저기 다리를 뻗고 있다는 것을 알 수 있다. $a_{10}$를 인풋으로 사용한 뉴런은 물론이고 이 뉴런이 내보낸 아웃풋을 사용한 뉴런 등 많은 것들이 영향을 받았을 것이다. 그래서 이번에는 아까처럼 다른 변수를 무시하거나 하는 짓은 못한다. 다 계산해줘야한다.

여기서 $\frac{\partial E}{\partial a_{10}}$이 의미하는 것은 마지막 레이어부터 a_10을 아웃풋으로 내보낸 뉴런이 속한 레이어의 바로 뒤 레이어까지 전파된 에러를 의미한다.

그리고 이 에러를 구성하는 $\frac{\partial E_1}{\partial a_{10}}$와 $\frac{\partial E_2}{\partial a_{10}}$ 등은 이렇게 구한다.

이 식에서 나타난 $\frac{\partial E_1}{\partial a_{20}}$과 $\frac{\partial E_2}{\partial a_{21}}$의 경우는 위에서 본 1번과 같은 케이스이므로 1번처럼 계산하면 될 것이다. 필자는 이 식을 코드로 구현할 때 헷갈렸던 부분이 하나 있었다.

한번 $\frac{\partial E_1}{\partial a_{10}}$을 구하는 공식을 보자. 뉴런이 가지고 있지 않은 변수가 2개 존재한다.

1. $E_1$: 뒤쪽 레이어에서 전파된 로스
2. $a_{10}$: 앞쪽 레이어 뉴런의 아웃풋

그래서 처음에는

뭐야, 이거 이터레이션할 때 앞뒤 레이어에 다 접근해서 가져와야하나? 예외처리도 두 번 해줘야하고 귀찮네…

라고 생각했었는데…

네, 생각해보니까 이 값은 그냥 이 뉴런이 받는 인풋이었습니다.

계속 변수에만 집중하다보니 놓치고있던 쩌는 사실이었다. 모자란 필자의 두뇌에 3초간 묵념한 후 다음 단계로 넘어갔다.

의사코드 작성

여기까지 생각이 든 후 간략한 의사코드를 먼저 작성했다. 원래는 연습장에 끄적끄적 작성했지만 여기서는 Syntax Highlighting을 위해 TypeScript 문법으로 작성하겠다.

기본적인 클래스는 Network, Layer, Neuron 총 3개로 생각했었고 Forward propagation만 Backpropagation만 어떻게 구현할 지 고민을 많이 했었기 때문에 의사코드도 Backpropagation에 관련된 코드만 작성했다.

Neuron

Neuron 클래스에서는 Backpropagation이 진행되면 Neuron 객체가 가지고 있는 Weight를 업데이트하고 이때 Forward Propagation 때 미리 계산해놓았던 $\frac{\partial a}{\partial z}$를 사용하여 뉴런의 아웃풋이 전파된 에러에 영향을 끼친 기여도인 $\frac{\partial E}{\partial a}$도 함께 계산해야한다.

class Neuron {
  private activationFunction미분값: number;
  private weights: number[]; // 뉴런의 Weight들
  private weight미분값들: number[]; // 뉴런의 인풋이 전체 에러에 영향을 끼친 기여도들

  public weight들업데이트 (에러미분꼴: number, 학습속도: number) {
    const 새로운weight들 = this.weights.map((weight, index) => {

      // wx값이 에러에 영향을 끼친 기여도를 구한다
      const loss = 에러미분꼴 * this.activationFunction미분꼴;

      // weight는 x가 wx값에 영향을 끼친 기여도와 같다.
      // loss랑 곱해주면 x가 에러에 영향을 끼친 기여도를 알 수 있다.
      this.weight미분값들[index] = loss * weight;

      // x는 weight가 wx값에 영향을 끼친 기여도와 같다.
      // loss랑 곱해주면 w가 에러에 영향을 끼친 기여도를 알 수 있다.
      return weight - (학습속도 * (loss * this.inputs[index]));
    });

    this.weights = 새로운weight들;
  }
}

Layer

Layer 클래스는 Backpropagation 때 이터레이션을 돌리면서 가지고 있는 뉴런들의 메소드를 호출한다.

이때 마지막 레이어라면 MSE의 미분값인 $-(target_i - output_i)$를, 마지막 레이어가 아니라면 다음 레이어에 있는 뉴런들의 weights 배열을 업데이트할 때 미리 계산해놓은 weights미분값들 배열에서 필요한 원소들을 가져와 모두 더한 후 현재 레이어의 Neuron들에게 전달해준다.

class Layer {
  public 다음레이어: Layer;
  private 뉴런들: Neuron[];

  public 뉴런들업데이트 (전파된에러들: any[], 학습속도: number) {
    if (다음레이어) {
      // 마지막 레이어가 아니기 때문에 넘어온 에러 중
      // 이 뉴런의 아웃풋과 함께 계산된 weight의 인덱스를 지정해서 사용해야한다.
      this.뉴런들.forEach((뉴런, index: number ) => {
        const loss = 전파된에러들.reduce((a: number, b: number[]) => a +_b[index], 0);
        neuron.updateWeights(loss, 학습속도);
      });
    }
    else {
      // 마지막 레이어라면 각 뉴런이 영향을 준 에러에 대한 기여도만 넘겨줘야 한다.
      this.뉴런들.forEach((뉴런, index: number) => {
        neuron.updateWeights(loss[index], 학습속도);
      });
    }
  }
}

메소드를 보면 현재 업데이트 할 레이어가 마지막 레이어가 아니라면 에러의 자료형이 number[]에서 number[][]으로 바뀐다. 그 이유는 뉴런 내에서 Weight들이 가지고 있는 index값이 있어야 계산이 편하기 때문이다.

[[wp_0_0, wp_0_1, wp_0_2], [wp_1_0, wp_1_1, wp_1_2]]

다음 레이어의 에러는 이런 2차원 배열 형태로 리턴된다. 이때 만약 레이어의 0번째 인덱스에 있는 뉴런의 weight들을 업데이트 하려고 한다면, 다음 레이어의 에러 중 이 뉴런과 연결되어있는 에러만 뽑아와야한다.

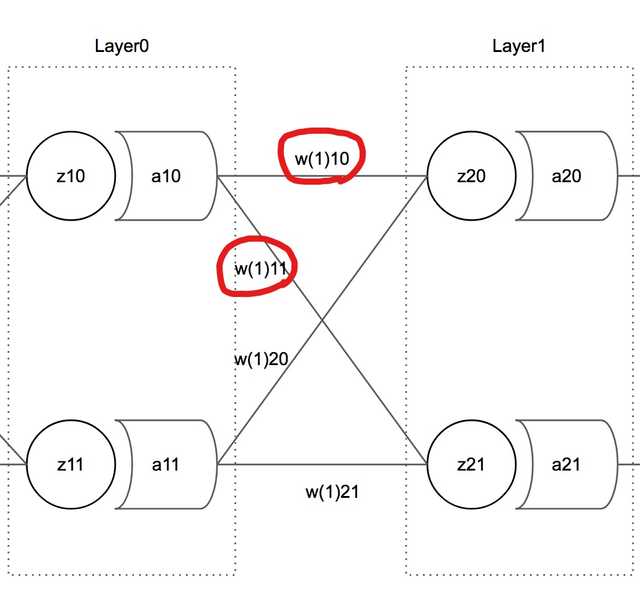
이 그림에서 보듯 $a_{10}$와 함께 계산에 사용된 Weight 변수는 다음 레이어에 있는 뉴런들의 weights 배열의 0번 원소로 저장되어 있다.

즉, 업데이트하고자 하는 뉴런의 인덱스가 0이면 다음 레이어에 있는 모든 Neuron.weights[0]에만 영향을 주었다고 할 수 있고 그렇기 때문에 참조해야하는 에러도 Neuron.weightPrimes[0]인 것이다.

Network

Network 클래스는 레이어와 뉴런의 생성, Forward propagation이나 Backpropagation 등 네트워크의 동작을 제어, 통합된 결과나 에러를 관리 정도의 책임을 가진다.

class Network {
  학습속도: number;
  레이어들: Layer[];
  인풋레이어: Layer;
  아웃풋레이어: Layer;
  전체에러미분값들: number[]; // -(target_i - output_i)들

  public backPropagation () {
    const 뒤집힌레이어들 = [...this.레이어들]reverse();
    const 학습속도 = this.학습속도;
    뒤집힌레이어들.forEach(레이어 => {
      let 에러들: any = [];

      if (레이어.id === this.아웃풋레이어.id) {
        에러들 = this.전체에러미분값들;
      }
      else {
        // Backpropagation이 진행 중이라 다음 레이어의 계산이 먼저 끝나있다.
        // private 멤버변수에 접근하면 에러나지만 의사코드니까 그냥 넘어가자
        에러들 = 레이어.다음레이어.뉴런들.map(뉴런 => 뉴런.weightPrimes);
      }
      레이어.뉴런들업데이트(에러들, 학습속도);
    });
  }
}

마무으리

대충 이렇게 작성이 되었다면 이제 메인 함수에서 이터레이션을 돌리면 된다.

const network = new Network();

for (let i = 0; i < 학습횟수; i++) {
  network.forwardPropagation();
  network.backPropagation();
  console.log(network.getResults());
}

뭐 대충 이런 식으로 하면 될 거 같다. Forward propagation은 그냥 이터레이티브하게 쭉쭉 계산만 하면 되므로 어렵지 않았지만 Backpropagation은 뭔가 직관적으로 와닿지 않아서 처음에 조금 힘들었다.

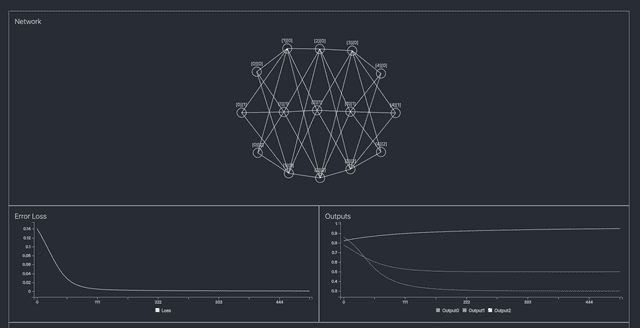소박하게 완성된 모습

그래도 어떻게든 세미나 시간에 맞춰서 네트워크 구현을 했고, D3를 사용해서 소박한 시각화도 하고나니 뿌듯하긴 했다. 다음에 시간나면 레이어마다 Activation Function을 변경할 수 있거나 Loss Function도 변경할 수 있게 개선해보고 싶다.

이상으로 TypeScript를 사용하여 간단한 인공 신경망 개발 삽질기 포스팅을 마친다. 전체 소스는 깃허브 레파지토리에서 확인할 수 있고 라이브 데모는 여기에서 확인 가능하다.