2017-05-06프로그래밍 / 그래픽스

[JavaScript로 중력 구현하기] 1. 중력이란 무엇일까?

이번 포스팅에서는 만유인력의 법칙을 이용하여 중력을 구현해보려고 한다. 지표면 상에서 한 방향으로 작용하는 중력이 아니라 랜덤한 질량을 가진 여러 개의 물체를 랜덤한 좌표에 뿌려놓고 서로의 운동에 어떻게 간섭하는 지를 살펴볼 수 있는 시뮬레이션을 만들어 볼 예정이다.

중력이란?

먼저 이 포스팅은 물리학도가 아닌 필자같이 수학에 익숙하지 않은 사람을 대상으로 한 포스팅이기에 먼저 중력의 개념부터 제대로 짚고 넘어가려고 한다.

뉴턴께서 가라사대, 중력이란 두 개의 질량을 가진 물체가 서로 끌어당기는 힘이라고 했다.

사실 뉴턴은 만유인력의 법칙이라는 공식을 만들면서 어떻게 중력이 작용하는지는 알아냈지만 왜 중력이 생기는 것인지는 몰랐다. 아무래도 “신께서만 아실 일이지…”하고 넘어간 듯 싶다. 그리고 뉴턴은 질량을 가진 물체가 중력을 가진다고 했었는데 이는 빛은 질량이 없기 때문에 중력에 영향을 전혀 받지않는다는 얘기가 된다.

하지만 현대에 와서 밝혀진 사실에 의하면 빛도 중력에 영향을 받는다. 영화 인터스텔라에서도 보지 않았던가? (100% 확실한 시각화 묘사라고는 할 수 없지만 이론물리학자인 킵 손이 일반상대성이론을 계산해서 3D로 시각화했다고 한다.)

블랙홀 같이 중력이 어마어마한 곳에서는 이 현상이 눈에 띄게 관찰되는데, 이를 중력렌즈효과라고 부른다.

블랙홀 뒤를 지나는 빛의 휘어짐

중력은 1915년 아인슈타인의 일반상대성이론에서 에너지에 의한 시공간의 휨으로 정의되게 된다. 그래서 시공간 상의 물체의 질량이 급격하게 증가하거나 감소할 때 시공간에 파동이 생기게 되는데 이것이 바로 작년 초에 발견된 중력파이다. 이렇게 발생된 중력파는 빛과 같은 속도로 움직인다고 한다. 그래서 갑자기 태양계에서 태양이 뿅!하고 사라지게 되면 태양 주위를 공전하던 행성들이 바로 궤도를 이탈해서 날아가는 게 아니다.

예를 들어서 지구같은 경우에는 태양에서 나온 빛이 지구까지 약 8분 20초 정도 걸리니까 태양이 갑자기 사라져도 8분정도는 없어진 태양이 있던 위치를 그대로 공전하는 것이다. 그러다가 8분 후 마지막에 태양에서 나온 빛이 지구에 도달하는 순간 지구는 궤도를 이탈할 것이다.

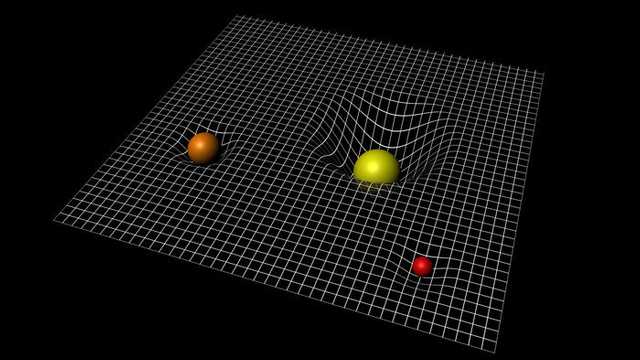큰 질량을 가진 물체일수록 시공간을 더 많이 휘게 만든다

그렇다고 만유인력의 법칙이 틀렸다는 것이 아니라, 상대성이론은 만유인력의 법칙이 놓친 점을 보완해준 것에 더 가깝다. 사실 중력이 아주 큰 공간(아주 많이 휘어진 공간)이 아니라면 만유인력의 법칙으로도 충분히 설명이 가능하다.

예를 들어 지구는 전체적으로 보면 커다란 구이지만 지구에 사는 우리가 주변을 돌아보면 이게 구인지 평면인지 알수가 없다. 이와 같이 휘어진 정도가 아주아주 작아 유클리드 공간과 거의 유사한 공간을 유사-유클리드 공간이라고 한다. 그리고 이런 유사-유클리드 공간에서는 만유인력의 법칙만 적용해도 충분하다. 아폴로 우주선을 달에 보낼때도 만유인력의 법칙만으로 충분했다고 한다.

결론적으로 중력을 구하는 것은 시공간의 곡률을 구하는 것으로 볼 수 있지만, 사실 필자가 만드려고 하는 간단한 시뮬레이션은 굉장히 작은 유사-유클리도 공간 안에서의 상황을 시뮬레이팅하는 것이고, 현실에 적용되는 프로그램이 아니라 말 그대로 시뮬레이션이기 때문에 만유인력의 법칙만으로도 충분히 구현이 가능하다.

그래서 구현은 어떻게?

일단 설명을 쉽게 하기 위해 랜덤한 질량을 가진 2개의 물체를 랜덤한 좌표에 랜덤한 방향과 속도를 가지게 설정한 후 그냥 공간 상에 뿌린다고 가정하자. 이 물체 2개의 중력의 영향을 계산하는 것은 그다지 어렵지 않다. 여기서 만유인력의 법칙이 등장한다.

F_{12} = -G{\frac{m_1 m_2}{\vert{r_{12}\vert}^2}}\hat{r_{12}}

이 공식은 물체1이 물체2에게 가하는 중력 $F$ 를 구하는 공식이다. 이 공식에서 $G$ 는 중력 상수를 의미하고, 이 중력 상수는 6.67384 * 10^-11로 정해져 있다.

그리고 분자의 $m_1$ 과 $m_2$ 는 각 물체의 질량이고 분모인 $r_{12}$ 은 이 물체들 간의 유클리드거리를 의미한다. 그리고 마지막에 곱해주는 $r$ 은 물체1에서 물체2를 바라보고 있는 단위벡터를 의미한다.

즉, 이 식은 분모에 물체 간의 거리가 들어가있고 분자에 두 물체의 질량이 들어가있다는 것이 포인트이다.

이는 두 물체 간의 거리가 멀어질수록 분모가 커지니까 결과 값이 작게 나오고, 두 물체의 질량이 커질수록 분자가 커지니까 결과 값이 크게 나온다는 것을 의미하며, 간단하게 말해서 중력은 두 물체 간 거리에 반비례하고 두 물체 간 질량의 곱에 비례한다라고 할 수 있다.

혹시 선형대수학을 안배우신 분들이 있을 지 모르니 간단하게 설명하면, 벡터라는 놈은 공간 상에서의 방향을 의미한다는 정도만 알아두셔도 좋을 것 같다. 지금 우리가 계산하려고 하는 공간은 3차원 공간이기 때문에 벡터는 (x, y, z) 3개의 좌표값을 가지게 된다.

우리가 어릴 때 배웠던 만유인력의 법칙은

F = G\frac{m_1 m_2}{r^2}

의 꼴을 가지는데 이 공식의 결과는 1 5.2 1204같은 스칼라 값을 가지게 된다. 스칼라는 어떠한 물리량만을 의미하는 것이기 때문에 중력이 얼마나 센지는 알 수 있어도 중력이 어느 방향으로 센지는 알 수가 없다.

그래서 힘의 방향을 표현해줘야 우리가 이 공식을 제대로 사용할 수 있고, 그렇기 때문에 마지막에 벡터를 곱해주는 것이다.

그리고 공식 맨 앞에 -1이 붙어있는 이유는 벡터의 방향 때문이다. 마지막에 우리가 곱한 벡터는 물체1 -> 물체2의 방향이다. 하지만 중력은 내 쪽으로 끌어당기는 힘이지 밀어내는 힘이 아니기 때문에 따라서 힘의 방향을 물체1 <- 물체2와 같이 반대로 바꿔줘야 하기 때문에 -1을 곱해주는 것이다.

조금 복잡해보이지만 막상 코드로 구현하면 간단하다. 필자는 ThreeJS를 사용하여 벡터 계산을 진행하였다.

import { Vector3 } from 'three';

function calcGravity(o1, o2, G) {
  // o1의 위치벡터와 o2의 위치벡터의 차를 구해 o1 -> o2를 바라보는 벡터를 구한다.
  let force = new Vector3().subVectors(o1.location, o2.location);
  
  // 위에서 구한 방향벡터의 길이를 구한 후 절대값으로 변환해준다.
  const distance = Math.sqrt(force.length() ** 2);
  
  // 위에서 구한 방향벡터를 단위벡터로 바꿔준다.
  force = force.normalize();
  
  // 중력 스칼라 구하기
  const strength = -(G * o1.mass * o2.mass) / (distance ** 2);
  
  // 방향벡터에 위에서 구한 중력 스칼라를 곱해준다
  force = force.multiplyScalar(strength);
  
  return force;
}

이제 여기서 나온 값을 계산 대상이 되는 현재 물체의 위치값에 계속 더해주면 물체는 그 방향으로 운동하게 될 것이다. 근데 문제는 실질적으로 우리는 2개만 뿌릴 것이 아니라는 것이다.

저 만유인력의 법칙은 2개의 물체 간의 중력 만을 생각하고 계산하고 있다. 그렇다면 여러 개의 물체의 중력이 서로에게 영향을 주고 받는 것도 계산할 수 있을까?

아쉽게도 이런 다체문제는 수리물리학분야에서 손꼽히는 난제이며, 1887년에 앙리 푸엥카레가 삼체 이상 문제의 일반해를 구하는 것이 불가능하다고 했다. 그래서 우리는 저 위에 있는 이체문제의 만유인력의 법칙을 사용해서 중력을 근사적으로 구하는 수 밖에 없다.

다음 포스팅에서는 간단한 중력 모델 샘플을 코드로 구현해볼 예정이다. 이상으로 JavaScript로 중력 구현하기 첫번째 포스팅을 마친다.

중력이란?

그래서 구현은 어떻게?

Evan Moon