2024-02-13프로그래밍

[번역] 프로그래머를 위한 카테고리 이론 - 3. 다양한 카테고리들

우리는 다양한 예시들을 연구해보면서 카테고리에 대한 진정한 이해에 한발짝 더 다가갈 수 있다. 카테고리는 매우 다양한 형태와 크기를 가지고 있기 때문에 종종 전혀 예상하지 못 했던 곳에서 나타나기도 한다. 일단 가장 간단한 것부터 한번 시작해보도록 하자.

3.1 대상이 없는 경우

가장 간단한 카테고리는 어떠한 대상이나 사상을 전혀 가지고 있지 않는 카테고리이다. 이 카테고리만 따로 떼놓고 본다면 별로 쓸모가 없어보이겠지만 다른 카테고리와의 관계에서는 매우 중요한 의미를 가질 수도 있다. 예를 들면 모든 카테고리를 대상으로 가진 카테고리와 빈 카테고리의 관계 같은 것들이 있다. 상상하기 어렵겠지만 이런 카테고리도 분명 존재한다. 만약 여러분이 공집합의 존재 의의에 공감한다면 빈 카테고리도 나름의 의미가 있지 않을까?

3.2 단순한 그래프

우리는 단순히 어떠한 대상을 화살표로 연결하는 것만으로도 카테고리를 만들어볼 수 있다. 한번 임의의 유향 그래프(Directed Graph)에 몇 개의 화살표를 추가하여 카테고리를 만드는 상상을 해보자. 먼저 그래프의 각 노드에 특정 대상으로부터 나와서 다시 자기 자신에게 돌아가는 항등 화살표를 추가한다. 그 다음 한 화살표의 종점 노드가 다른 화살표의 시작 노드와 일치하는 경우에는 이 두 화살표가 합성 가능하다는 사실을 의미하므로, 그 화살표들의 합성을 의미하는 새로운 화살표를 추가한다.

항등 화살표를 제외하면 우리는 항상 새로운 화살표를 추가할 때마다 추가된 화살표와 다른 화살표들과의 합성 여부에 대한 것들을 고려해야 한다. 이러다보면 무한히 많은 화살표들이 생기겠지만 뭐 딱히 문제는 없다.

즉 이러한 과정을 통해 우리는 모든 그래프의 노드들은 대상을, 그리고 간선은 합성 가능한 사상을 표현하는 일종의 카테고리를 만들었다고 볼 수 있다. (항등 사상의 경우에는 길이가 0인 특별한 간선이라고 볼 수 있다.)

이렇게 미리 주어진 그래프에서부터 생성된 카테고리는 자유 카테고리(Free Category)라고 불린다. 즉, 미리 주어진 구조에 최소한의 항목만을 추가하여 원하는 법칙을 만족시킬 수 있는 일종의 자유 구성인 것이다. 여기서 우리가 원하는 법칙이란 결국 카테고리의 법칙일 것이다. 이와 관련된 자세한 내용은 추후 더 알아보도록 하자.

3.3 차수

자 그러면 이제 완전히 다른 예시를 한번 살펴보자. 이번 카테고리는 대상들간의 사상이 “작거나 같음”으로 나타나는 관계를 가진 카테고리이다.

먼저 이것이 정말 카테고리가 될 수 있는지부터 확인해보자. 항등 사상이 존재하는가? 모든 대상은 자기 자신보다 작거나 같으므로 답은 참이다. 사상의 합성은 존재하는가? 만약 $a≤b$ 이고, $b≤c$ 라면 $a≤c$ 일테니 답은 참이다. 합성 간의 결합법칙은 적용되는가? 이도 참이다. 이와 같은 관계를 가진 집합은 원순서(Preorder)라고 하는데, 원순서 집합 또한 카테고리의 모든 조건을 만족시키므로 원순서 집합도 카테고리라고 할 수 있다.

그럼 여기에 몇 가지 조건을 추가하여 더 강한 관계를 만들어보자. 만약 $a≤b$ 이고 $b≤a$ 라면 $a$ 와 $b$ 가 같을 수 밖에 없는 경우도 있다. 이러한 관계는 부분순서(Partial Order)라고 한다.

또한 우리는 어떠한 두 대상이 서로 상호 관계를 가진다는 조건도 부여할 수 있다. 이 경우에는 전순서(Linear Order 또는 Total Order)라는 개념을 얻을 수 있다.

자 그럼 이제 이 순서 집합들을 한번 카테고리로 표현해보도록 하자. 원순서 집합은 어떤 대상 a에서 다른 대상 b로 향하는 사상이 최대 1개만 존재하는 카테고리이다. 이러한 카테고리는 “Thin”하다고 표현하며, 원순서 집합은 Thin 카테고리라고 볼 수 있다.

어떠한 카테고리 $C$ 가 가진 대상 $a$ 에서 대상 $b$ 로 향하는 사상들의 집합은 Hom 집합(Hom-set)이라고 하며, $C(a,b)$ 또는 $Hom_c(a,b)$ 라고 표기한다.

즉, 원순서 집합에 속한 모든 Hom 집합은 공집합이거나 하나의 원소만을 가지는 단일원소집합이다. 이는 $C(a,a)$ 로 표현되는 $a$ 에서 $a$ 로 향하는 사상 집합인 항등사상 집합 또한 예외는 아니며, 이 집합은 어떤 원순서 집합 내에서도 단 하나의 원소, 즉 항등사상(identity) 하나만을 가지고 있다.

이러한 원순서 내에서는 한 대상에서 시작한 여러 사상을 거쳐 동일한 대상으로 돌아오는 사이클이라는 개념이 성립할 수 있지만, 부분순서 내에서는 이러한 사이클이 성립될 수 없다.

💡 역주

원순서와 다르게 부분순서는 $a≤b$ 이고 $b≤a$ 라면 $a$ 와 $b$ 는 같다는 반대칭관계를 만족해야한다. 대상이 a,b 밖에 없는 카테고리를 상상해보자. 사이클이라는 개념이 성립하려면 a→b로 향하는 사상과 b→a로 향하는 사상이 존재해야 한다. 원순서는 a→b로 향하는 사상과 b→a로 향하는 사상이 있다고 해서 이 두 대상을 같은 것이라고 정의하지 않아도 되지만, 부분순서는 반대칭관계를 만족해야하기 때문에 반드시 a=b가 되어버린다.

즉, a와 b가 다른 대상이 될 수가 없으므로 사이클을 정의할 수가 없다.

정렬 문제와 같은 일상적인 문제를 해결할 때 퀵 정렬, 버블 정렬, 병합 정렬과 같은 정렬 알고리즘은 오직 전순서에서만 제대로 작동하며 부분순서에서는 위상 정렬 알고리즘을 사용해야 하기 때문에 어떠한 카테고리가 원순서인지 부분순서인지 또는 전순서인지를 알아내는 능력은 프로그래머에게 매우 중요하다고 할 수 있다.

3.4 집합으로써의 모노이드

모노이드(Monoid)는 굉장히 간단하지만 놀라울 정도로 강력한 개념이다. 모노이드는 덧셈과 곱셈과 같은 기본적인 산술 연산의 기반이 되는 개념이며, 문자열, 리스트, Fold 연산이 가능한 구조, 동시성 프로그래밍에서의 Future, 함수형 반응형 프로그래밍에서의 이벤트 등 다양한 프로그래밍 기법에서도 빈번하게 사용되는 개념이다.

전통적으로 모노이드는 이항연산을 가진 집합으로 정의된다. 이 이항연산은 결합법칙을 만족시켜야 하며, 이 연산에 대해서 항등원과 같은 역할을 하는 특별한 원소가 하나 있어야 한다. 예를 들어 0을 포함하는 자연수 집합( $\mathbb{N}_0$ )은 덧셈에 대해 모노이드를 이룬다.

결합법칙은 아래와 같은 특성을 의미한다.

(a + b) + c = a + (b + c)

이건 다른 말로 하면 수를 더할 때 식 내에 있는 괄호를 생략해도 괜찮다는 의미이다. 그리고 덧셈에 대한 항등원은 0인데, 이 또한 결합법칙을 통해 간단하게 확인해볼 수 있다.

0 + a = a
a + 0 = a

여기서 두 번째 식은 결국 첫 번째 식과 같은 의미이다. 덧셈은 a + b = b + a 와 같은 교환법칙도 만족하는 연산이기 때문이다. 하지만 교환법칙은 모노이드에서 반드시 만족시켜야 하는 대상은 아니다.

예를 들어 문자열 연결 연산(Concatenation)의 경우 교환법칙을 만족하지 않지만 모노이드이다. 문자열 연결 연산의 항등원은 빈 문자열이고 이는 문자열의 어느 쪽에 가져다 붙여도 문자열을 변경하지 않기 때문이다.

Haskell에서는 모노이드에 대한 타입 클래스를 정의할 수 있다. 이는 mempty라고 불리는 항등원과 mappend라고 불리는 이항연산을 정의한 타입이다.

class Monoid m where
    mempty  :: m
    mappend :: m -> m -> m

지금은 두 개의 인자를 받는 함수를 m->m->m 이라는 타입으로 표현한 것이 조금 어색하게 보일 수 있겠지만, 이건 나중에 커링(Currying)에 대해서 배우면 완벽하게 이해할 수 있을 것이다.

이렇게 여러 화살표가 있는 타입 선언은 보통 두 가지 방식으로 해석해볼 수 있다. 첫째로는 오른쪽에 있는 타입이 반환 타입이 되는 다인수 함수로 해석할 수 있으며, 두 번째로는 가장 왼쪽에 있는 첫 번째 인수를 받아 함수를 반환하는 함수로도 해석해볼 수 있다. 후자의 해석은 m -> (m -> m) 처럼 괄호를 추가해서 강조해볼 수는 있지만, 사실 애초에 연산순서가 오른쪽에서 왼쪽으로 흘러가기 때문에 의미없는 괄호이기는 하다. 이러한 해석 방식에 대해서는 잠시 후 다시 이야기해보도록 하겠다.

여기서 우리가 주의해야 할 점은 Haskell에서 mempty가 항등성을 가져야한다는 것과 mappend가 결합법칙을 만족시켜야 한다는 사실을 명시적으로 표현할 수 있는 방법이 없다는 것이다. 이런 법칙들을 만족시키고 준수하는 것은 전적으로 프로그래머의 책임에 달려있다.

Haskell의 클래스는 C++의 클래스처럼 강제적이지 않다. 그래서 새로운 타입을 정의할 때도 굳이 해당 클래스를 미리 지정할 필요가 없으며, 주어진 타입이 어떤 클래스의 인스턴스가 되는지에 대한 것은 나중에 정의해도 된다.

예를 들어 String에 mempty와 mappend를 구현해서 모노이드가 되었다고 가정해보겠다. (사실 이건 Standard Prelude에 이미 구현되어있기는 하다.)

instance Monoid String where
    mempty = ""
    mappend = (++)

결국 String은 그저 문자들의 리스트일 뿐이므로, 위 예시에서는 리스트 연결 연산자인 (++)를 사용했다.

여기서 Haskell의 문법에 대해서 하나 짚고 넘어가야 할 것 같다. Haskell에서 임의의 중위 연산자를 괄호로 감싸면 두 개의 인자를 받는 함수가 된다. 즉 두 문자열을 연결하기 위해 우리는 아래와 같이 문자열 사이에 ++ 연산자를 넣어주거나,

"Hello " ++ "world!"

또는 ++ 연산자를 괄호로 감싸 (++)로 표현하여 함수로 만들고 두 개의 인자를 넘기는 방식으로 코드를 작성할 수 있다.

(++) "Hello " "world!"

이때 함수의 인자들은 쉼표로 구분되지도 않고 괄호로 감싸지도 않았다는 사실을 기억하도록 하자. (이게 바로 Haskell을 배울 때 가장 익숙해지기 어려운 부분인 것 같다.)

또한 Haskell에서는 함수가 서로 같다는 동등성을 표현할 수 있다는 점을 이야기하고 넘어가면 좋을 것 같다. 아래 예시를 보도록 하자.

mappend = (++)

위 코드는 함수가 생성한 값의 비교를 표현하는 것과는 개념적으로 다른 표현이다.

mappend s1 s2 = (++) s1 s2

위 두 가지 예시 중 전자는 Hask 카테고리 또는 연산이 종료되지 않음을 의미하는 bottom을 제외한 집합에서의 사상의 동등성을 표현하고 있다고 볼 수 있다. 이러한 등식은 간결할 뿐 아니라 다른 카테고리에도 일반화될 수 있다.

후자의 경우는 확장 동등성(Extensional Equality)라고 불리며, mappend 함수와 (++) 함수가 인자로 동일한 두 개의 문자열을 입력받았을 때 이 함수들이 반환하는 출력 또한 동일하다는 것을 의미한다. 인수의 값은 점(Point)이라고 불리기도 하기 때문에 이 개념을 점별 동등성(Point-wise Equality)이라고 부르기도 한다. 인수를 지정하지 않은 함수들의 동등성은 Point-Free하다고 한다.

참고로 Point-Free 스타일을 표현할 때 주로 함수의 합성(Composition)을 사용하는데, 이때 함수의 합성은 점(.)을 사용하여 표현하므로, 초보자에게는 조금 헷갈릴 수 있다.

💡 역주

mappend = (++)가 표현하는 동등한 사상이라는 개념과 mappend s1 s1 = (++) s1 s2 가 표현하는 Extensional Equality의 개념이 조금 어려울 수 있다. 사실 잘 생각해보면 두 함수가 같은 인자를 받았을 때 같은 값을 반환한다는 것이 이 함수들이 정말로 “같은 함수”라는 것을 의미하는 것은 아니다.

예를 들어 (a, b) ⇒ a + b 처럼 두 인자를 받아 두 값을 더해주는 함수와 (a, b) ⇒ a + b + 0 처럼 항등원을 한번 더 더하는 함수는 같은 인자를 받았을 때 항상 같은 값을 반환할테지만, 엄연히 두 함수의 구현은 다르므로 “다른 함수”라고 보는 것이다.

즉, “같은 함수”라는 개념은 단지 같은 인자를 받았을 때 같은 값을 반환하는 것만으로는 만족할 수 있는 개념이 아니기 때문에 이 두 가지 개념을 엄밀하게 구분하는 것이다.

C++에서 모노이드를 가장 비슷하게 흉내낼 수 있는 방법은 현재 표준 제안 단계인 concepts 키워드를 사용하는 것이다.

template<class T>
  T mempty = delete;

template<class T>
  T mappend(T, T) = delete;

template<class M>
  concept bool Monoid = requires (M m) {
    { mempty<M> } -> M;
    { mappend(m, m); } -> M;
  };

첫 번째 정의는 마찬가지로 표준 제안 단계인 Value Template 기능을 사용하며, 다형적인 값을 받아들일 수 있도록 선언하여 모든 타입을 커버할 수 있도록 작성하였다.

그리고 delete 키워드는 기본값이 정의되어 있지 않다는 것을 의미하며, 이는 각 케이스 별로 모두 명시해줘야 한다. 즉 위 예시에서 mappend의 경우는 기본값이 정의되지 않은 것이다.

concept으로 정의된 Monoid는 주어진 임의의 타입 M에 대해서 mempty와 mappend가 적절하게 정의되었는지를 검사하는 구문이기 때문에 bool을 반환하도록 작성되어있다.

이러한 Monoid concept은 아래와 같이 적절한 특수화와 오버로딩을 통해 인스턴스로 구현할 수 있다.

template<>
std::string mempty<std::string> = {""};

std::string mappend(std::string s1, std::string s2) {
    return s1 + s2;
}

3.5 카테고리로써의 모노이드

자 지금까지 우리에게 익숙한 원소를 가진 집합의 관점에서 모노이드를 정의해보았다. 그러나 이 책은 카테고리 이론에 대한 이야기를 하고 있기 때문에, 이제부터는 집합과 원소에서 벗어나 대상과 사상에 대해 이야기를 해보려고 한다.

자 일단 관점을 조금 바꿔서, 이항연산을 적용한다는 것을 어떤 대상에서 다른 대상으로 “이동”하는 것으로 생각해보자.

예를 들어 모든 자연수에 5를 더하는 연산을 생각해보자. 이 연산은 0을 5로, 1을 6으로, 2를 7로 매핑할 것이다. 이런 개념은 일종의 자연수 집합에 정의된 함수와 동일하다. 역시 함수와 집합으로 생각하니 편하고 좋은 것 같다.

어떤 수 n에 대해서 다시 n을 더하는 “Adder”라는 함수가 있다고 생각해보자. 이 Adder는 어떤 방식으로 합성될까? 5를 더하는 함수와 7을 더하는 함수를 합성하면 12를 더하는 함수가 될 것이다. 즉, Adder들간의 합성은 덧셈의 규칙을 그대로 유지한다고 볼 수 있다. 그렇다면 덧셈이라는 개념을 함수의 합성이라고 생각해도 문제가 없을 것이다.

그리고 항등원인 0을 다루는 Adder도 존재할 수 있다. 0을 더한다는 행위는 아무것도 바꾸지 않는다는 의미이니 결국 자연수 집합에서의 항등함수라고 봐도 좋을 것 같다.

즉, 전통적인 덧셈의 규칙들 대신에 Adder 함수들을 합성하는 규칙을 사용한다고 해도 연산 과정에서 딱히 어떤 정보를 잃어버리는 일은 없다는 말이다. 함수의 합성은 결합법칙을 만족하기 때문에 Adder의 합성 또한 결합법칙을 만족할 것이니 말이다. 그리고 항등함수에 해당하는 0을 더하는 Adder까지 존재한다.

여기서 눈치 빠른 독자분들이라면 정수를 Adder로 매핑하는 것이 mappend 의 두 번째 해석이었던 m->(m->m)의 타입 선언과 유사하다는 것을 알아차릴 수 있었을 것이다. 이는 mappend가 모노이드 집합의 한 원소를 해당 집합에 작용하는 함수로 매핑한다는 것을 의미한다.

자 이제 자연수 집합 같은 것들은 다 잊어버리고, 그냥 이 집합을 Adder라는 수많은 사상이 달린 하나의 대상이라고 생각해보자. 결국 모노이드는 단 하나의 대상을 가진 단일대상 카테고리이다. 모노이드라는 이름 또한 단일한 무언가를 의미하는 그리스어 mono에서 유래되었다. 모든 모노이드는 단 하나의 대상과 서로 적절하게 합성할 수 있는 여러 사상들로 이루어진 단일대상 카테고리라고 할 수 있다.

문자열 연결 연산은 굉장히 흥미로운 경우인데, 우리는 연결하려고 하는 문자열을 대상 문자열의 뒤쪽에 붙힐 것인지, 앞쪽에 붙힐 것인지 선택할 수 있기 때문이다. 이 두 가지 모델의 합성 테이블(Composition Table)은 마치 거울처럼 대칭적이다.

이는 “foo” 뒤에 “bar”를 추가하여 “foobar”를 만드는 것과 “bar” 앞에 “foo”를 추가하여 “foobar”를 만드는 것이 결국 동일하다는 것을 통해 확인해볼 수 있다.

그렇다면 이제 “모노이드라는 단일대상 카테고리가 어떤 이유로 이항연산자를 가진 집합과 연결되는가”에 대한 질문이 나올 차례인 것 같다.

우리는 단일대상 카테고리에서 사상의 집합이라는 하나의 집합을 뽑아낼 수 있다. 위의 예시와 연결해보자면 이 집합의 원소인 사상들은 Adder들일 것이다. 다시 말해 우리는 카테고리 $M$ 의 단일대상 $m$ 의 Hom 집합인 $M(m,m)$ 을 얻게되는 것이다.

이 집합에서의 이항연산은 쉽게 정의해볼 수 있는데, Hom 집합 내 두 원소 간의 모노이드 곱은 각 사상들의 합성에 해당하는 원소일 것이다. 만약 $M(m,m)$ 에서 $f$ 와 $g$ 에 해당하는 두 원소를 가지고 모노이드 곱 이항연산을 한다면 결과는 $g\circ f$ 라는 것이다.

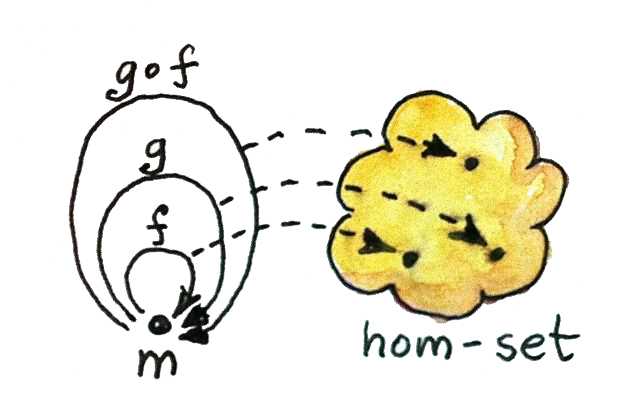
결국 이 사상들의 출발 대상과 도착 대상은 모두 동일한 대상이기 때문에 이러한 합성 또한 항상 존재할 수 밖에 없다. 그리고 카테고리의 규칙에 따라 사상 간의 합성은 결합법칙을 만족하며, 항등 사상이 모노이드 곱 연산의 항등원이라고 볼 수 있다. 즉 우리는 항상 모노이드 카테고리에서 모노이드 집합을 만들어낼 수 있으며, 이 두 개념은 본질적으로 같은 것이라고 볼 수 있다.

다만 여기에는 수학자들이 지적할만한 작은 문제가 하나 있는데, 반드시 사상들이 집합을 이뤄야 할 필요는 없다는 것이다. 카테고리의 세계에서는 집합보다 더 거대한 개념들이 있다. 임의의 두 대상 간의 사상이 집합을 이루는 카테고리를 작은 카테고리(Locally Small Category)라고 한다. 물론 앞서 이야기했듯이 필자는 이러한 사소한 부분들은 무시하고 넘어갈 것이지만, 이런 개념이 있다는 것 정도만 알아두자는 차원에서 언급해보았다.

카테고리 이론에서 흥미롭게 여겨지는 많은 개념들은 Hom 집합의 원소가 합성이 가능한 사상임과 동시에 어떤 집합의 원소로써의 성질도 가질 수 있다는 점에서부터 비롯된다. 즉, 카테고리 $M$ 이 가진 사상들의 합성은 사상들의 집합인 $M(m,m)$ 이 가진 원소(사상)들 간의 모노이드 곱이라고 해석할 수도 있다.

원문 보기

👉 Category Theory for Programmers