Is the Randomness Your Computer Creates Actually Random?
Mid-Square Method, Linear Congruential Method, Mersenne Twister — the secrets behind random number generation algorithms

In this post, I want to talk about randomness. Randomness refers to a pattern where, when events occur, there’s no discernible regularity between one event and the next — a truly arbitrary sequence. The computers we use also need to generate random patterns from time to time, and they do.
But a computer is really just a fancy calculator. A calculator takes input values, juggles them around, and spits out a result. So how can such a machine produce random outcomes? Before we answer that question, we need to think about what randomness fundamentally is. Does true randomness even exist?
What Is Randomness?
As I mentioned above, randomness is a pattern that occurs without any discernible order.
People may have different associations, but the first thing that comes to my mind is gambling. The most dangerous thing about gambling is the hope that “sure, I lost this round, but I could win the next one!” — and that hope stems from the belief that gambling games are fundamentally based on randomness. In other words, there has to be a significant element of luck involved.
The thing is, I don’t know much about actual gambling games, so let me use something lighter as an example — a coin-flipping game. Imagine placing coins on a thick book, then slapping the book to try to flip them. The idea is that whoever flips all the coins to show the same face wins the pot. It’s hard to calculate exactly how many of the coins will flip when you slap the book, which makes it a game with a reasonable degree of randomness — and that’s what gives it the element of chance essential to gambling.
So let me throw out that opening question again:
Is this truly random?
Even though it seems random, if you think about it, the game still operates within the laws of physics. If you knew the weight of each coin, the force of the slap, and the elasticity of the book, you could theoretically calculate which coins would flip. Of course, that kind of calculation isn’t easy — so even though it’s not random in the purest sense, we just say “close enough, let’s call it random.”
In other words, true randomness is surprisingly rare even in our everyday lives. We just think things are random.
Randomness in Computers
Just as we label things “random” in daily life when they have a reasonable degree of unpredictability, computers don’t generate true randomness either — they produce a convincing enough level of unpredictability and call it random. On top of that, creating something on a computer requires defining rules, and the very idea of using rules to generate rule-less randomness is a contradiction.
That’s why all we can really create is pseudo-random — something that’s not truly random but close enough. And since computers are fundamentally number-crunching calculators, generating random events requires the ability to produce random numbers.
So how do computers actually generate these random numbers?
Mid-Square Method
The Mid-Square Method is a pseudo-random number generation technique devised by John von Neumann in 1949. The idea is simple: take a number, square it, then extract a portion from the middle of the result to use as the next random number.
Let’s say we want to generate 4-digit random numbers, starting with 1234:
| Phase | Input | Squared | Random Number |
|---|---|---|---|
| 0 | 1234 | 1522756 | 1522756 |
| 1 | 5227 | 27321529 | 27321529 |
| 2 | 3215 | 10336225 | 10336225 |
You keep extracting the middle digits and squaring them to generate the next random number. It’s pretty obviously predictable, right? Well, this was developed in the 1950s when von Neumann was active, and computers of that era were painfully underpowered, so the simplest possible approach was necessary. That’s why this method is rarely used today.
Linear Congruential Method
The Linear Congruential Method is the algorithm used by C’s rand function. It’s defined by the following recurrence relation and returns a sequence of random numbers:
Here, is the sequence of random numbers and the rest are just arbitrary integers. For reference, the ANSI C standard specifies . Let’s implement this in JavaScript:
let m = 2 ** 31;
const a = 1103515245;
const c = 12345;
function rand (x) {
return (((x * a) + c) % m);
}
function getRandomNumbers (randCount = 1) {
// Use the current time as the initial seed.
const initial = new Date().getTime();
const randomNumbers = [initial];
for (let i = 0; i < randCount; i++) {
randomNumbers.push(rand(randomNumbers[i]));
}
randomNumbers.shift();
return randomNumbers;
}
console.log(getRandomNumbers(10));Paste this into your browser console and run it — you’ll get an array of random numbers with the length you specified as the argument.
(10) [1163074432, 465823232, 1719475776, 1744670976, 790949120, 552540416, 896259328, 1473241344, 1074855168, 575793408]A key characteristic of the Linear Congruential Method is that it uses the previously generated random number to produce the next one, and since it has at most possible values, it has a maximum period of before repeating. That’s why I declared the m variable with let. Try assigning a small number to m in your browser console and calling getRandomNumbers again — you’ll notice duplicate values appearing much more frequently.
The Linear Congruential Method has been widely used in computers since the early days because the computation is extremely simple and fast. However, it has a periodic cycle and correlations exist between generated numbers, meaning that if you know the last generated number and the other variables, you can predict all subsequent numbers.
The problem is that those variables are defined by the ANSI C standard, so anyone can look them up. In other words, anyone with a bit of knowledge can observe the output of rand and predict the next random number.
That’s why this algorithm is mainly used in situations where it doesn’t matter if the random numbers are predicted, or in constrained environments like embedded systems where memory is limited.
Mersenne Twister
The Mersenne Twister is a random number generation algorithm used in Excel, MATLAB, PHP, Python, R, C++, and many others. It was developed in 1997 by Makoto Matsumoto and Takuji Nishimura. The name comes from the fact that the algorithm’s period is a Mersenne prime.
“Mersenne prime” might sound fancy, but it’s actually straightforward. A Mersenne number is — just 2 to the power of n, minus 1. A Mersenne prime is simply a Mersenne number that happens to be prime.
The most commonly used variant is “MT19937,” which has a period of . C++ also uses this algorithm. Here’s a simplified overview of how it works:
- Use a seed to generate a vector of length 624. The seed is usually derived from hardware noise or the current date.
- Use this vector to produce 624 pseudo-random numbers.
- Apply noise to the vector and repeat step 2. This noise application is called “twisting.”
The twisting step uses a technique called GFSR (Generalized Feedback Shift Register). There isn’t much accessible material on GFSR — most of it is academic papers — so I wasn’t able to dig into it deeply. But after some extensive Googling and poring over papers, I found that it appears to be a variation of LFSR (Linear Feedback Shift Register). (Information was so limited that I’m not 100% certain it’s LFSR-based.)
LFSR takes previous state values, runs them through a linear function, and uses the result to generate the next value. The function typically used is XOR, and the initial value is called the seed.
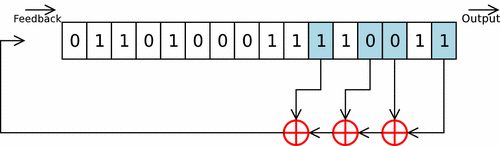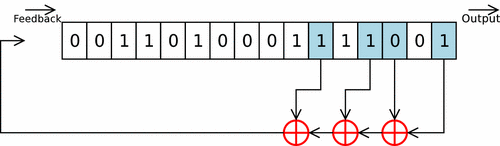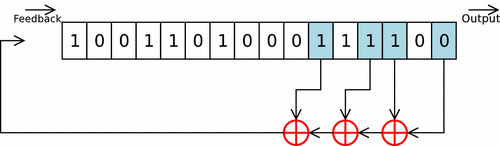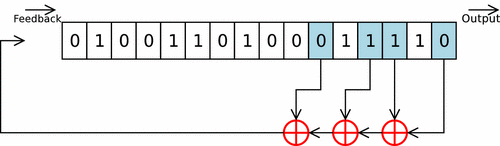
Here’s a brief explanation of LFSR: you designate a few memory addresses and push an initialized input (the seed) into the register. The bits shift one position to the right, and you get one bit popping out at the end as output. Then you access the pre-designated memory addresses, extract their values, and pass them through three XOR gates in sequence to produce the next input, which you push back into the register. Repeat.
Since the Mersenne Twister uses GFSR — a slight variation of LFSR — to generate random numbers, it also requires an initial seed.
For the detailed algorithm, check the Wikipedia article on Mersenne Twister - Algorithmic detail. I ported the C implementation of MT19937 — which Matsumoto and Nishimura revised and improved in 2002 — to JavaScript. This code is designed for 32-bit random numbers. There’s a separate 64-bit version called MT19937-64.
const N = 624;
const M = 397;
const F = 1812433253;
const UPPER_MASK = (2 ** 32) / 2; // 0x80000000
const LOWER_MASK = UPPER_MASK - 1; // 0x7fffffff
const MATRIX_A = 0x9908b0df;
class MersenneTwister {
constructor () {
const initSeed = new Date().getTime();
this.mt = new Array(N);
this.index = N + 1;
this.seedMt(initSeed);
}
seedMt (seed) {
let s;
this.mt[0] = seed >>> 0;
for (this.index = 1; this.index < N; this.index++) {
this.mt[this.index] = F * (this.mt[this.index - 1] ^ (this.mt[this.index - 1]) >>> 30) + this.index;
this.mt[this.index] &= 0xffffffff;
}
}
int () {
let y;
const mag01 = new Array(0, MATRIX_A);
if (this.index >= N) {
let kk;
if (this.index === N + 1) {
this.seedMt(5489);
}
for (kk = 0; kk < N - M; kk++) {
y = (this.mt[kk] & UPPER_MASK) | (this.mt[kk + 1] & LOWER_MASK);
this.mt[kk] = this.mt[kk + M] ^ (y >>> 1) ^ mag01[y & 1];
}
for (; kk < N - 1; kk++) {
y = (this.mt[kk] & UPPER_MASK) | (this.mt[kk + 1] & LOWER_MASK);
this.mt[kk] = this.mt[kk + (M - N)] ^ (y >>> 1) ^ mag01[y & 1];
}
y = (this.mt[N - 1] & UPPER_MASK) | (this.mt[0] & LOWER_MASK);
this.mt[N - 1] = this.mt[M - 1] ^ (y >>> 1) ^ mag01[y & 1];
this.index = 0;
}
y = this.mt[this.index++];
y ^= (y >>> 11);
y ^= (y << 7) & 0x9d2c5680;
y ^= (y << 15) & 0xefc60000;
y ^= (y >>> 18);
return y >>> 0;
};
}The constants used in the code — F = 1812433253, MATRIX_A = 0x9908b0df, this.seedMt(5489) — aren’t numbers I chose arbitrarily. They’re standard coefficients defined in the MT19937 specification.
Honestly, the algorithm is so complex that I don’t fully understand all of it myself. (The price of not studying harder in college…) Still, writing it out as code gives you a much better grasp than just reading about it, which is why I ported the original C code to JavaScript. The C library code I referenced can be found here.
const rand = new MersenneTwister();
console.log(rand.int()); // 2145258025Running the code, it seems to generate random numbers just fine. To properly verify randomness you’d need to visualize the results and examine the distribution, but I’ll skip that for now. By the way, if you visit the homepage of Makoto Matsumoto, who created this algorithm, you can find the story behind how it got its name:
Makoto: Professor Knuth says it’s too hard to pronounce the name.
Takuji: …[A few days later]
Makoto: Hey Takun, how about Mersenne Twister? It uses Mersenne primes, and the original is a Twisted GFSR (Generalized Feedback Shift Register).
Takuji: Hmm…?
Makoto: Doesn’t it sound like a roller coaster? It sounds fast, it’s easy to remember, and easy to pronounce. And here’s a secret — our initials are hidden in the name! (Makoto, Takuji)
Takuji: …
Makoto: Come on, let’s go with MT!
Takuji: …Fine.Later, we received a letter from Professor Knuth saying “it seems like a good name.”
You can really feel the dynamic between the bubbly Makoto and the deadpan Takuji. It’s nice to see that even the creators of such a brilliant algorithm have this very human side to them.
XOR Shift
XOR Shift, like the Mersenne Twister, is a pseudo-random number algorithm based on LFSR. You could think of it as a lighter alternative to the Mersenne Twister — the principle is similar, but the implementation is much simpler and faster, so it sees plenty of use.
There are several variants of the XOR Shift algorithm, using 32-bit, 64-bit, or 128-bit numbers, with periods of , , and (all Mersenne numbers) respectively.
The problem was that it couldn’t pass TestU01, a random number quality testing framework. Passing TestU01 is a requirement for becoming an ANSI C standard.
This led to several variant algorithms, one of which is XOR Shift 128+ — an improvement on the 128-bit XOR Shift 128. (Sounds like a video game sequel title…)
As it happens, XOR Shift 128+ is the random number generation algorithm adopted by major JavaScript engines including V8, SpiderMonkey, and JavaScriptCore. This algorithm was presented by Sebastiano Vigna at a conference in November 2016. The paper can be found here.
The overall principle is similar to the LFSR I explained above, so let’s look at how V8 implements Math.random. The original code is written in C++, but I’ve ported the same logic to JavaScript so you can easily run it in your browser.
V8’s XOR Shift 128+ algorithm can be found in v8/src/base/utils/random-number-generator.h.
// xorshift128plus.js
const state = [1827981275, 1295982171];
function xorshift128plus () {
let s1 = state[0];
let s0 = state[1];
state[0] = s0;
s1 ^= s1 << 23;
s1 ^= s1 >> 17;
s1 ^= s0;
state[1] = s1;
console.log('Current register state -> ', state);
return state[0] + state[1];
}
console.log('Initial register state -> ', state);
for (let i = 0; i < 5; i++) {
console.log('Random number -> ', xorshift128plus());
}Initial register state -> [ 1827981275, 1295982171 ]
Current register state -> [ 1295982171, 867440954 ]
Random number -> 2163423125
Current register state -> [ 867440954, 1393243966 ]
Random number -> 2260684920
Current register state -> [ 1393243966, 37812574 ]
Random number -> 1431056540
Current register state -> [ 37812574, 833890405 ]
Random number -> 871702979
Current register state -> [ 833890405, 1661667227 ]
Random number -> 2495557632Looking at the output, you can see how the register state changes over time.
The value at index [1] moves to index [0], a new random number is placed at index [1], and the two elements are added together for the output.
When inserting the new value at index [1], it uses the shifted-out value from index [0] to perform XOR shifting, then places the result back at index [1].
The shifting constants 23 and 17 were discovered through research during the development of the XOR Shift 128+ algorithm — they’re the optimal constants found through testing. The paper includes detailed tables comparing the results of various different constants they tried.
Wrapping Up
I originally started this post thinking it would be a light discussion about randomness, but it ended up being heavier on the math than I expected.
The truth is, generating truly random numbers with a computer — which is just a calculator — is virtually impossible. Recently, researchers in the US reportedly succeeded in generating true random numbers using a quantum computer, but quantum computing is still a distant reality for most of us, so I’ll leave that aside.
I’m not exactly a math enthusiast myself. But seeing the many people who have taken on the challenge of creating orderless random numbers through mathematical research, I feel genuinely grateful as someone who comfortably codes at higher abstraction layers. (I could never do what they do…)
 If the researchers build the foundational algorithms, I'll put them to good use in production applications...!!!
If the researchers build the foundational algorithms, I'll put them to good use in production applications...!!!
While writing this post, I spent a lot of time staring at papers and Wikipedia — my brain is overloaded from too much English and too many formulas. And the Mersenne Twister in particular… seriously, it’s insanely complex.
By the way, Makoto Matsumoto, who created it, is currently an associate professor at Hiroshima University’s mathematics graduate school. It makes me wonder just how brilliant you have to be to stand at that podium. A completely different level…
That wraps up this post on whether the randomness computers create is actually random.
References
XorShift - Wikipedia
There’s Math.random(), and then There’s Math.random() - V8 Dev
Further scramblings of Marsaglia’s xorshift generators - Sebastiano Vigna
The Xorshit128+ random number generator fails BigCrush - Daniel Lemire
관련 포스팅 보러가기
Simplifying Complex Problems with Math
Programming/AlgorithmHeaps: Finding Min and Max Values Fast
Programming/AlgorithmEfficiently Calculating Averages of Real-Time Data
Programming/Algorithm[Implementing Gravity with JavaScript] 2. Coding
Programming/Graphics[Implementing Gravity with JavaScript] 1. What is Gravity?
Programming/Graphics