SVG와 삼각 함수로 도넛 차트 만들어보기
    프로그래밍 / 그래픽스

    SVG와 삼각 함수로 도넛 차트 만들어보기

    이번 포스팅에서는 얼마 전에 필자가 삽질했던 내용인 SVG로 도넛 차트 그려보기에 대해서 이야기해볼까 한다. 사실 도넛 차트를 그리는 것 자체는 SVG가 제공하는 circle 엘리먼트를 사용하면 되기 때문에 간단하게 만들 수 있지만, 필자가 삽질했던 부분은 바로 애니메이션이었다.

    물론 chartjs나 nivo같은 차트 라이브러리를 사용하면 쉽게 도넛 차트를 사용할 수 있기는 하지만, 사실 필자에게 필요한 건 막대 차트와 도넛 차트 뿐이었기 때문에 이런 라이브러리를 사용하는 것이 과하다는 생각이 들었고, 결정적으로 이 정도 차트는 그냥 캔버스나 SVG로 대충 그려서 뚝딱하면 될 것 같다는 생각에 직접 구현하는 것으로 방향을 잡았다.

    사건의 발단

    // 원래는 이런 인터페이스를 가지고 있었다
<DoughnutChart size={40} rate={80} />

    사건의 발단은 바로 이렇게 생긴 도넛 차트였다. 사실 이 녀석은 필자가 맡고 있는 특정 서비스에서만 사용하고 있던 녀석이라서 굉장히 안일한 인터페이스를 가지고 있던 녀석이었지만, 최근 다른 곳들에서 이 녀석을 사용해야하는 니즈가 늘어나게 되면서 이 인터페이스를 조금 더 추상화해야할 일이 생겼다.

    기존 인터페이스는 빈 도넛차트에 1개의 데이터를 rate라는 퍼센테이지 값을 사용하여 렌더하는 방식이었기 때문에, 도넛 차트에 들어오는 데이터가 반드시 하나라는 가정이 성립되어야만 사용할 수 있는 인터페이스였다.

    하지만 이 도넛 차트를 여러 곳에서 자유롭게 사용할 수 있게 하려면 1개 데이터가 아니라 여러 개의 데이터를 시각화할 수 있게 변경해야했고, 이 과정에서 도넛 차트의 로직과 애니메이션 또한 뜯어고칠 수 밖에 없었다.

    도넛 차트 그리기

    사실 SVG 도넛 차트를 그리는 것 자체는 circle 엘리먼트와 stroke를 조합하면 꽤나 간단하게 해결할 수 있다. 한번 간단하게 SVG로 동그라미를 그려보도록 하자.

    <svg width="500" height="500" viewBox="0 0 100 100">
  <circle cx="50" cy="50" r="20" fill="transparent" stroke="blue" stroke-width="10" />
</svg>
    circle

    SVG 상에서 아무런 단위를 붙히지 않은 숫자는 암묵적으로 px 단위로 정의된다. 필자는 width와 height가 500px인 정사각형의 박스를 렌더하고 viewBox="0 0 100 100"을 사용하여 이 뷰박스 내부 세계에는 가로 100px 세로 100px을 가진 좌표를 정의한 것이다.

    만약 viewBox 속성을 사용하지 않았다면 SVG는 자동으로 width와 height에 주어진 값만큼의 픽셀을 가진 뷰박스를 렌더했을테지만, 좌표가 0 ~ 100으로 떨어지는 편이 도형의 좌표를 생각하기 더 쉬우므로 이렇게 정의한 것이다.

    즉, 실제 우리 눈에 보이는 이 박스의 크기는 가로세로 500px이지만 내부적으로는 100 x 100의 좌표계로 동작한다. 이후 필자는 이 뷰박스의 중심인 (50px, 50px)을 기준으로 지름이 20px이고 선 굵기가 10px인 원을 렌더했다.

    그리고 이 원 자체가 하나의 데이터가 차트의 100%를 차지하고 있는 도넛 차트라고 볼 수 있다. 도넛 차트는 이렇게 SVG의 circle 엘리먼트 만으로도 기본적인 모양을 잡을 수 있기 때문에 시각화 자체가 그렇게 어려운 편은 아니다.

    하지만 도넛 차트라고 하면 하나의 데이터가 아니라 여러 개의 데이터를 동시에 시각화 할 수 있어야할텐데, 그렇다면 여러 개의 데이터를 표현하고 싶다면 어떻게 해야할까?

    여러 개의 데이터를 시각화해보자

    도넛 차트는 결국 하나의 도넛 도형을 각 데이터가 부분부분 나누어 가지고 있는 형태의 그래프이다. 즉, 데이터 별로 원의 일부분을 차지하고 있는 모양을 그려줘야 한다는 이야기이다.

    doughnut 하나의 데이터가 원의 각 부분부분을 차지하고 있다

    다행히도 SVG는 선을 그릴 때 점선(대시)을 표현할 수 있는 stroke-dasharray라는 속성을 제공하고 있기 때문에 어떤 데이터를 얼마나 그려줄 것이냐를 표현하고 싶을 때 이 속성을 이용하면 된다.

    <circle
  cx="50"
  cy="50"
  r="20"
  fill="transparent"
  stroke="blue"
  stroke-width="2"
  stroke-dasharray="10 5"
/>

    stroke-dasharray는 숫자와 공백으로 구분되는 일련의 데이터 셋을 전달받아 점선을 정의하며, 첫 번째 인자는 선을 얼마나 그릴 것인지를 결정하고 두 번째 인자는 공백을 얼마나 그릴 것인지를 결정한다. 즉, 위 예제 코드는 10px 만큼 선을 그리고 5px만큼 공백을 그리는 것을 반복하기 때문에 이런 결과를 볼 수 있을 것이다.

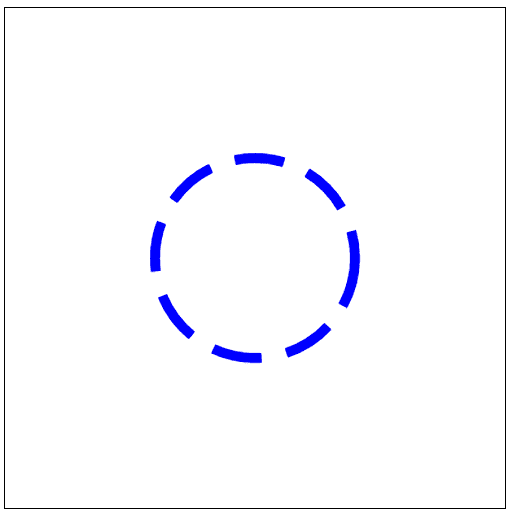    dasharray 10px의 선, 5px의 공백이 반복된 점선이 표현된 모습

    즉, 이 속성을 사용하여 원의 일부분만을 차지하는 선을 하나 그린 후 나머지는 공백으로 두는 점선을 표현한다면 도넛 차트에서의 여러 데이터의 표현이 가능한 것이다.

    하지만 위 예제를 자세히 보면 원의 오른쪽 부분에 있는 선의 길이가 다른 곳에 비해서 더 긴 것을 확인할 수 있다. 그 이유는 필자가 stroke-dasharray 속성에 넘긴 저 숫자가 원주의 길이와 정확히 맞아떨어지는 숫자가 아니기 때문이다.

    stroke-dasharray 속성은 렌더할 선과 공백의 길이, 즉 px 단위의 값을 받는 녀석이다. 그 말인 즉슨 점선을 딱 떨어지게 그리고 싶다면 원주의 길이, 즉 원의 둘레 길이를 먼저 알아낸 후에 이 길이에 정확히 나누어 떨어지는 값들을 넣어줘야 한다는 것이다.

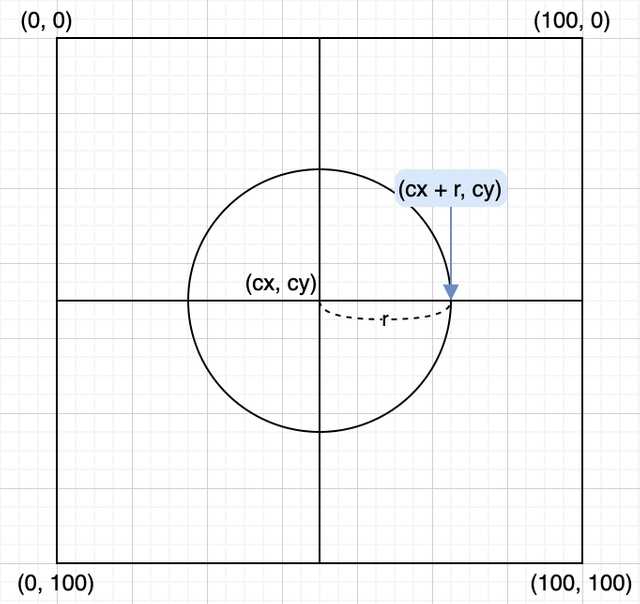
    SVG는 원을 그릴 때 원점의 오른쪽 방향인 (cx + r, cy) 좌표를 기준점으로 삼아서 원을 렌더한다. 그래서 stroke-dasharray를 사용하여 점선을 렌더할 때 원이 끝나는 지점과 정확히 아다리가 맞지 않는다면 위 예제처럼 원의 오른쪽 부분의 점선만 길어보이는 현상이 발생할 수 있는 것이다.

    원주의 길이를 구하는 공식은 초심플한 2πr2\pi{r}이기 때문에 그냥 Math.PI 상수를 사용하여 쉽게 구할 수 있다.

    const radius = 20;
const diameter = 2 * Math.PI * radius;
console.log(diameter); // 125.66370614359172

    필자는 이 원의 반지름을 20px으로 설정했으니 원주의 길이는 약 126px이지만, 이 값을 stroke-dasharray에 넣었던 값들의 합인 15로 나누어 보면 8.37이 나오며 정확히 나누어 떨어지지 않는다. 그래서 점선이 8번 반복되고 남은 0.37 만큼은 어정쩡하게 시작점에 붙어있는 형태로 렌더되는 것이다.

    즉, 도넛 차트에 여러 데이터를 제대로 시각화하고 싶다면 기본적으로 다음 두 가지 정보들이 필요하다.

    1. 원주의 길이(2πr2\pi{r})
    2. 도넛 차트에 그릴 데이터와 총 합의 비율
    const radius = 20;
const diameter = 2 * Math.PI * radius;

const dataset = [9, 5, 4, 3, 1];
const total = dataset.reduce((r, v) => r + v, 0);

dataset.forEach(data => {
  const ratio = data / total;
  const strokeLength = diameter * ratio;
  const spaceLength = diameter - strokeLength;
  console.log(`stroke-dasharray = ${strokeLength} ${spaceLength}`);
});
    stroke-dasharray = 51.4078797860148 74.25582635757692
stroke-dasharray = 28.559933214452663 97.10377292913907
stroke-dasharray = 22.847946571562133 102.81575957202959
stroke-dasharray = 17.135959928671596 108.52774621492013
stroke-dasharray = 5.711986642890533 119.95171950070119

    이처럼 원주의 길이와 각 데이터의 비율, 이 두 가지 정보를 이용하면 각 데이터가 원주의 어느 정도의 비율을 차지하고 렌더할 지를 정의할 수가 있다.

    하지만 이 정보들만 가지고 차트를 렌더하려고 하면 한 가지 문제가 발생하는데, 바로 데이터들이 렌더되는 기준점이 전부 (cx + r, cy) 좌표라는 것이다.

    blog Page 9

    그래서 아무리 데이터를 렌더할 선의 길이를 제대로 구했다고 해도 모든 데이터가 렌더링되는 기준점이 동일하기 때문에 당연히 이대로 렌더링을 해버린다면 이런 슬픈 모양의 차트가 그려지게 된다.

    doughnut failed 정체를 알 수 없는 무언가가 연성되었다

    도넛 차트는 각 데이터가 누적되어 최종적으로는 하나의 원을 그리는 차트기 때문에 한번 데이터를 렌더하고 나면 그 다음 데이터가 렌더될 시작점을 지금까지 렌더된 데이터들의 총 합만큼 밀어줘야한다.

    다행히도 SVG는 stroke-dashoffset 속성을 통해 점선이 시작되는 부분을 변경할 수 있는 기능을 제공하고 있기 때문에 우리는 그냥 잘 계산만 해서 이 속성에 알맞은 값을 넣어주면 된다.

    const dataset = [9, 5, 4, 3, 1];

// 각 데이터를 누적하여 저장하고 있자!
const acc = dataset.reduce((result, value) =>
  [...result, result[result.length - 1] + value],
  [0]
);

console.log(acc);
    [0, 9, 14, 18, 21, 22]

    첫 번째 데이터가 렌더될 때는 시작점을 밀어줄 필요가 없기 때문에 오프셋이 0이어야한다. reduce 함수의 두 번째 인자는 누산을 시작할 때 사용하는 초기 값을 의미하므로 여기에 그냥 0을 담은 배열을 넘겨주면 된다.

    그리고 초기 값으로 0을 이미 담고 있는 배열을 넘기기 때문에 누산된 값들을 담고 있는 배열은 데이터셋 배열보다 길이가 1만큼 더 긴데, 사실 배열의 가장 마지막 원소인 22는 필요가 없는 값이다.

    왜냐하면 이 값들은 데이터가 렌더될 시작점을 정의하는 값들이기 때문이다. 맨 마지막 원소인 22는 데이터 셋의 총 합과 동일한 값이기 때문에 도넛 차트의 모든 데이터의 렌더가 끝났음을 의미하는 값이라, 만약 acc[i] === total과 같은 논리식으로 “렌더 끝났어?” 같은 조건을 정의할 게 아니라면 사실 쓸 데가 없다.

    이렇게 데이터 셋의 값을 누산하고 나면 데이터 셋의 값에 해당하는 차트를 렌더한 후 (acc[i] / total) * diameter와 같은 공식을 사용하여 정확히 몇 px만큼 오프셋 해야하는 지를 알 수가 있게 된다.

    const radius = 20;
const diameter = 2 * Math.PI * radius;

const dataset = [9, 5, 4, 3, 1];
const total = dataset.reduce((r, v) => r + v, 0);
const acc = dataset.reduce((result, value) =>
  [...result, result[result.length - 1] + value],
  [0]
);

dataset.forEach((data, i) => {
  const offset = (acc[i] / total) * diameter;
  console.log(`stroke-dashoffset = ${-offset}`);
});
    stroke-dashoffset = 0
stroke-dashoffset = -51.4078797860148
stroke-dashoffset = -79.96781300046746
stroke-dashoffset = -102.8157595720296
stroke-dashoffset = -119.9517195007012

    물론 굳이 reduce 함수를 사용하지 않고 let을 사용하여 계속 차트를 렌더할 때마다 지금까지 그린 선들의 길이를 계속 더하며 재할당해도 상관은 없다. 어찌되었든 포인트는 “내가 지금 어디까지 렌더를 했느냐”를 알고 있는 것이기 때문이다.

    그리고 위 예시에서 필자는 오프셋 값에 - 부호를 줘서 값을 반전시키고 있는데, 이건 SVG가 기본적으로 선을 렌더하는 방향이 반시계 방향이기 때문이다.

    상식적으로는 우리가 그리는 도넛 차트 데이터의 시작점부터 끝점까지 진행되는 방향이 시계 방향이기 때문에 SVG도 시계 방향으로 선을 렌더할 것 같지만, 사실 SVG는 그딴 거 신경쓰지 않는다.

    지금 이 도넛 차트에서는 데이터가 시계 방향으로 쌓이고 있지만 좌표를 어떻게 정의하냐에 따라서 반시계 방향도 얼마든지 가능하지 않은가? 이렇게 좌표의 위치가 변경될 때마다 렌더하는 방향을 바꾸는 것은 꽤나 비효율적이기 때문에 SVG는 기본적으로 무조건 반시계 방향으로 선을 그린다.

    이 개념은 밑에서 후술할 호에서도 똑같이 적용되기 때문에 이 사실을 기억하고 있으면 호를 렌더하는 방법에 대해서 조금 더 이해가 쉬울 것이라고 생각한다. 이렇게 SVG가 선을 그리는 방향을 쉽게 알아보기 위해서는 원이 아니라 라인으로 그려서 테스트해보면 된다.

    <line stroke-dasharray="5" stroke-dashoffset="0" x1="10" x2="90" y1="10" y2="10" stroke="#000" />
<line stroke-dasharray="5" stroke-dashoffset="3" x1="10" x2="90" y1="20" y2="20" stroke="#000" />
    line offset plus 오프셋을 3으로 주면 밑에 있는 선이 왼쪽으로 3px만큼 밀린다 
    <line stroke-dasharray="5" stroke-dashoffset="0" x1="10" x2="90" y1="10" y2="10" stroke="#000" />
<line stroke-dasharray="5" stroke-dashoffset="-3" x1="10" x2="90" y1="20" y2="20" stroke="#000" />
    line offset minus 오프셋을 -3으로 주면 밑에 있는 선이 오른쪽으로 3px만큼 밀린다

    이제 여기까지 파악했다면 원주를 따라 어느 정도만큼 데이터를 렌더할 것인지와 누적되어 표현되는 데이터를 렌더하기 위해 몇 px만큼 선의 시작점을 밀어줘야 할 지를 stroke-dasharray와 stroke-dashoffset 속성을 사용하여 자유롭게 표현할 수 있다.

    전체 코드로 보자!

    <!-- 100 x 100 짜리 뷰 박스를 그린다 -->
<svg viewBox="0 0 100 100" id="svg"></svg>
    const radius = 20; // 차트의 반지름
const diameter = 2 * Math.PI * radius; // 차트의 둘레
    const colors = ['#ddd', '#bbb', '#aaa', '#888', '#666'];
const dataset = [9, 7, 5, 3, 1];

// 전체 데이터셋의 총 합
const total = dataset.reduce((r, v) => r + v, 0);

// 데이터셋의 누적 값
const acc = dataset.reduce((arr, v, i) => {
  const last = arr[arr.length - 1];
  return [...arr, last + v];
}, [0]);

// 프로퍼티 할당 노가다 시작...
const svg = document.getElementById('svg');
dataset.forEach((data, i) => {
  const ratio = data / total;
  const fillSpace = diameter * ratio;
  const emptySpace = diameter - fillSpace;
  const offset = (acc[i] / total) * diameter;
  
  const circle = document.createElementNS('http://www.w3.org/2000/svg', 'circle');
  circle.setAttribute('cx', '50');
  circle.setAttribute('cy', '50');
  circle.setAttribute('r', String(radius));
  circle.setAttribute('fill', 'transparent');
  circle.setAttribute('stroke', colors[i]);
  circle.setAttribute('stroke-width', '10');
  circle.setAttribute('stroke-dasharray', `${fillSpace} ${emptySpace}`);
  circle.setAttribute('stroke-dashoffset', String(-offset));
  
  svg.appendChild(circle);
});
    doughnut 완성된 도우넛 차트!

    호를 사용하여 애니메이션을 만들어보자

    자, 이렇게 해서 원하는 데이터셋을 자유롭게 사용해서 이쁜 도넛 차트를 렌더할 수 있게 되었다. 하지만 진짜 복병은 도넛 차트 렌더 따위가 아니였다. 다시 한번 필자가 구현했던 차트를 보자.

    .
    .
    .
    um ㅓ...이쁜 애니메이션이 들어가있다

    물론 이런 애니메이션을 구현하는 방법이 엄청 다양한 것은 아니라서, 결국 최대한 가볍게 만드려면 크게 두 가지 정도의 방법이 나온다.

    1. SVG의 clippath나 mask를 사용한다
    2. 각 데이터를 렌더할 때 stroke-dasharray와 stroke-offset 속성에 애니메이션을 준다

    사실 이것도 어느 정도 정답은 정해져있는 고민인데, 2번 방법처럼 각 데이터마다 stroke-dasharray과 stroke-offset에 애니메이션을 적용한다는 것은 결국 도넛 차트의 각 부분마다 애니메이션을 따로 따로 정의해서 적용하겠다는 의미이다.

    하지만 첫 번째 데이터의 렌더 애니메이션이 끝나고 바로 이어서 두 번째 데이터의 렌더 애니메이션이 매끄럽게 재생되도록 만드는 건 꽤나 번거로운 일이다. (결국 개별로 수행되는 애니메이션이기 때문에 아무리 타이밍을 잘 맞춰도 뭔가 삐그덕거릴 확률이 높다)

    그런 이유로 필자는 1번 방법인 클립패스를 선택했는데, 처음에는 그냥 “차트 그릴 때랑 비슷한 원리로 클립패스를 그리면 되는거 아니야?”라고 생각했지만 나중에 알고 보니 여기도 지옥길이었다.

    circle 엘리먼트를 사용하지 못한다

    지옥길의 시작은 바로 circle 엘리먼트를 사용하지 못한다는 것을 깨달았을 때였다. 이 애니메이션은 특정 시작점으로부터 시계방향으로 원을 쭈욱 렌더하는 녀석이기 때문에 당연히 circle 엘리먼트로 그릴 수 있을 것이라고 생각했었지만, 조금 더 생각해보니 저건 원이 아니다.

    즉, 이 애니메이션은 마지막 애니메이션이 종료되었을 때만 원이 될 뿐이지 애니메이션이 진행되는 중간 과정은 원이 아니기 때문에 circle 엘리먼트로는 구현이 불가능한 것이다.

    도넛 차트를 그릴 때처럼 stroke-dasharray와 stroke-offset 속성을 사용하면 안되냐고 할 수도 있지만 본래 clippath 기능은 도형의 면과 면이 겹쳐지는 부분을 마스킹하는 것이기 때문에 선을 렌더하는 속성인 stroke-* 속성으로는 마스킹을 구현할 수가 없다.


    이 애니메이션은 이런 도형들을 하나하나 렌더하며 진행된다

    애니메이션이 진행되는 중간 과정의 도형들은 원이라고 정의할 수가 없는 녀석들이다. 원은 애초에 원점으로 부터 일정한 거리만큼 떨어진 점들의 집합으로 정의되는데, 중간에 있는 저 쥐가 파먹은 도형들은 이 정의가 들어맞지 않기 때문이다.

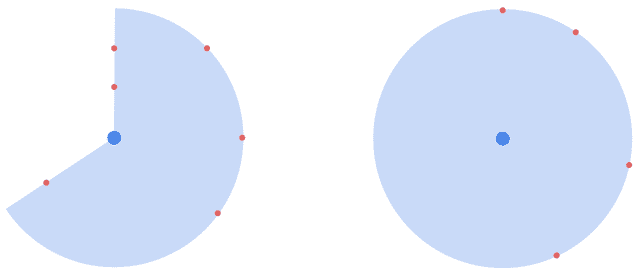
    arc render animation

    위 그림을 보면 오른쪽 도형은 원점에서 도형의 선에 놓여진 점들과의 거리가 모두 동일하지만, 왼쪽 도형은 원점과 도형의 선에 놓여진 점들과의 거리가 모두 동일하지는 않다. 즉, 오른쪽 도형은 “원점으로 부터 일정한 거리만큼 떨어진 점들의 집합”이라는 조건을 만족하기 때문에 원이 되는 것이고 왼쪽 도형은 원주의 일부분을 의미하는 호인 것이다.

    이 예시에서는 원을 기준으로 호를 그렸기 때문에 헷갈릴 수 있지만 호는 원의 일부분이 아니라 원주의 일부분이라고 정의된다. 원주는 꼭 원이 아니라 타원이더라도 가질 수 있는 것이므로 호의 모양도 굉장히 가지각색으로 나올 수 있게 된다.

    결국 호는 원이 아니기 때문에 circle 엘리먼트로는 이 클립패스 애니메이션을 구현할 수 없다.

    SVG가 호를 렌더하는 원리를 알아보자

    SVG는 호를 그리기 위한 별도의 엘리먼트를 제공하지는 않지만 path 엘리먼트에 A라는 명령어를 사용함으로써 호를 정의할 수 있는 기능을 제공하고 있다.

    a rx ry x축-회전각 큰-호-플래그 쓸기-방향-플래그 dx dy
    <path d="
  M 50 50
  A 45 45, 0, 1, 0, 275 125
  L 275 80 Z
"/>

    이렇게만 보면 호를 그리는 것이 간단할 것 같지만 생각보다 이 녀석이 렌더되는 원리가 직관적이지는 않다. 일반적으로 사람이 호라는 도형을 보면 단순히 그 원의 일부라고 생각하기 때문에 호의 중심각을 먼저 생각하게 되지만 저 인터페이스를 보면 알 수 있듯이 그 어디에도 각도를 의미하는 인자는 없다.

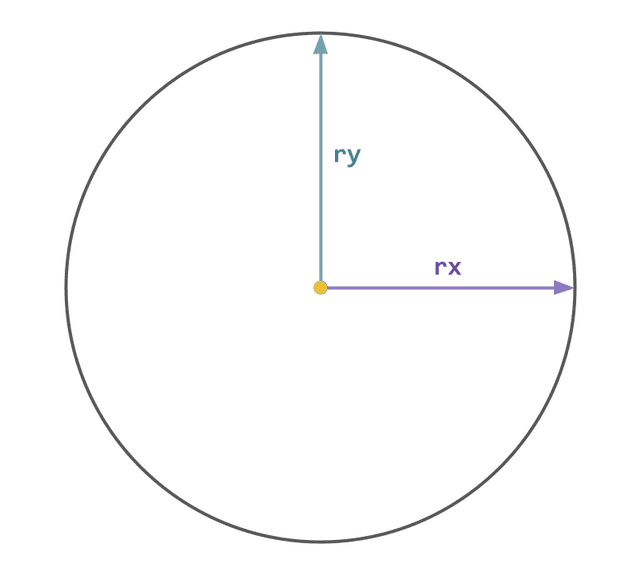
    사실 SVG가 호를 렌더하는 과정도 좌표 평면 상에 원을 정의하는 것부터 시작되기는 한다. 앞서 이야기 했듯이 호라는 도형은 원주의 일부이기 때문에 호를 그리려면 일단 원부터 그려야하기 때문이다.

    이때 정의되는 원은 A 명령어의 첫 번째 인자인 rx와 ry로 정의된다. 원인데 반지름을 받는 게 아니라 굳이 x와 y축 길이를 받는 이유는 앞서 말했듯이 호는 원의 일부분이 아니라 원주의 일부분을 의미하기 때문에 타원을 기준으로 그릴 수도 있기 때문이다.

    어찌되었던 원도 결국은 타원의 일종이므로 A 명령어는 추상적인 인터페이스를 위해 타원의 x축 반지름과 y축 반지름을 받도록 설계되어 있다. 하지만 호를 이해하기 위해서 반드시 예시가 타원일 필요는 없으므로, 조금 더 이해하기 쉽도록 모든 예시는 원으로 설명을 하도록 하겠다.

    일단 이런 가상의 원을 그리면서 SVG가 호를 렌더하는 과정이 시작된다

    이때 주의해야할 점은 이때 호가 그려지기 시작하는 시작점은 원의 중심이 아니라는 것이다. 다시 필자가 위에서 예시로 들었던 path 엘리먼트 예제를 보면 원의 중심점을 정하는 인자가 없는 것을 알 수 있다.

    <path d="
  M 50 50
  A 45 45, 0, 1, 0, 275 125
  L 275 80 Z
"/>

    이 명령어 집합은 M 50 50이라는 명령어로 시작하게 되는데, path 엘리먼트의 M 명령어는 렌더 시작점을 임의의 위치로 옮기는 Move를 의미하는 명령어이다.

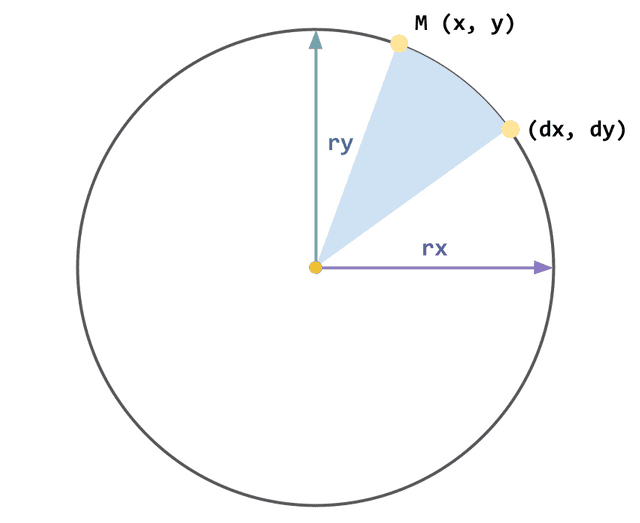
    하지만 이 위치는 원의 중심점이 아니라 호를 그리기 시작할 렌더 시작점을 의미한다. 즉, 이 호는 (50, 50) 좌표부터 A 명령어의 마지막 인자인 (dx, dy) 좌표까지 그려지게 되며, 이때 rx, ry에 의해 정의된 가상의 원주를 따라서 호가 그려지는 것이다.

    알아보기 쉽게 호를 면으로 표현했지만
    실제로는 x,y 부터 dx,dy로 이어지는 호의 머리 부분의 선만 렌더된다

    여기까지가 SVG가 호를 그리는 가장 기본적인 원리이다. 하지만 문제는 (x, y)와 (dx, dy)를 잇는 방법이 하나가 아니라는 것이다. 호라는 것은 그저 원주에 놓여있는 두 점을 원주를 따라서 이어주기만 하는 것이기 때문에 특정 방향으로만 그려야한다는 법이 없다.

    그래서 SVG는 (x, y)와 (dx, dy)라는 점을 원주에 위치시킬 수 있는 두 개의 원을 사용하여 호를 정의한다.

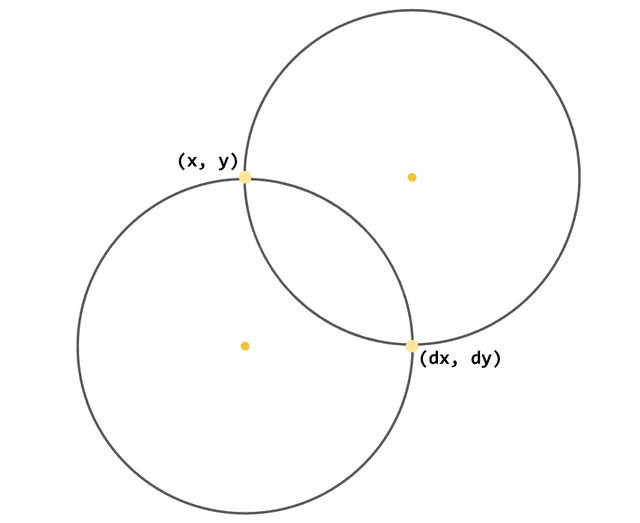    arc with circle (x, y)와 (dx, dy)를 동시에 원주에 위치시킬 수 있는 원은 단 두 개 뿐이다

    이때 두 개의 원의 원주에 위치한 (x, y)와 (dx, dy) 점들을 사용하여 호를 만들 수 있는 방법은 총 4개가 나오게 되는데, 이때 어떤 호를 그릴 지를 위 예시의 “큰 호 플래그”와 “쓸기 방향 플래그”로 결정하게 되는 것이다.

    a rx ry x축-회전각 큰-호-플래그 쓸기-방향-플래그 dx dy

    호의 플래그 이해하기

    백문이 불여일견이니 이번에도 한번 직접 그려보면서 호가 그려지는 과정과 저 플래그들이 정확히 어떤 일을 하는 것인지 이해해보도록 하자. 도넛 차트를 그릴 때와 마찬가지로 좌표에 대한 이해가 쉽도록 이번에도 가로 100, 세로 100의 좌표를 가진 뷰박스를 그리고 간단한 호를 한번 그려보도록 하겠다.

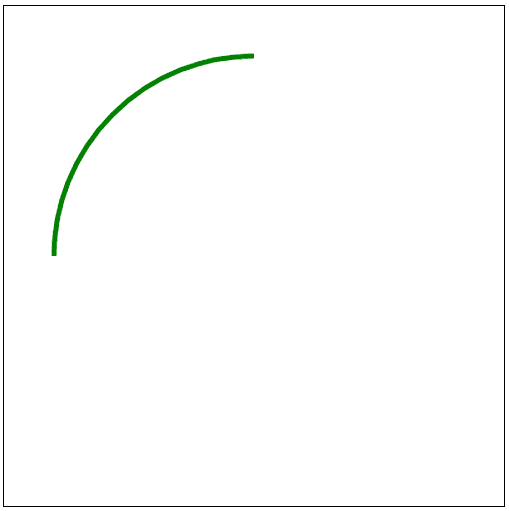
    <svg width="500" height="500" viewBox="0 0 100 100">
  <path d="
    M 50 10
    A 40 40, 0, 0, 0, 10 50"
    stroke="green"
    fill="transparent" />
</svg>
    1. (50, 10)으로 렌더 시작점을 옮긴다.
    2. rx, ry를 모두 40으로 할당하며 반지름이 40인 원을 정의한다.
    3. 회전각 0, 큰 호 플래그 0, 쓸기 방향 플래그 0으로 설정한다.
    4. 끝점 (10, 50)까지 호를 그린다.

    현재 필자가 설정한 큰 호 플래그와 쓸기 방향 플래그는 모두 0이기 때문에 SVG는 기본적으로 두 점을 이을 수 있는 작은 호를 그리며, SVG가 선을 그리는 방향인 반시계 방향으로 그릴 수 있는 호를 그린다.

    회전각 같은 경우는 호의 기준이 되는 원을 얼마나 기울일 것이냐를 의미하는데, 어차피 이 예시는 한 쪽으로 길쭉한 타원이 아니기 아니라 모든 반지름이 동일한 원이기 때문에 기울이는 것이 의미가 없다.

    어쨌든 이 명령어들을 사용하여 호를 그리면 실제로 이런 모양의 이쁜 호가 그려지는 것을 확인할 수 있다.

    arc 0 0

    쓸기 플래그

    비록 호의 플래그는 두 개 밖에 없지만 이 값이 바뀔 때마다 호의 모양이 휙휙 바뀌기 때문에 SVG가 정확히 어떤 방식으로 호를 그리는 것인지 잘 이해하고 있지 않다면 동작이 난해하다고 느껴질 수도 있다.

    하지만 아까 필자가 이야기했던 SVG가 선을 그리는 방향이 기본적으로 반시계 방향이라는 것만 기억하고 있다면 사실 그렇게 어려운 동작은 아니다.

    필자가 위에서 렌더했던 호를 조금 더 자세하게 다시 그려보자면 사실 이런 모양이다.

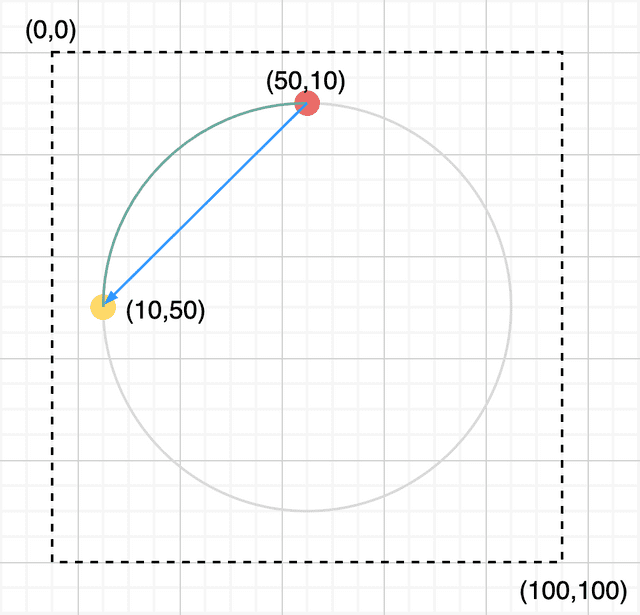    arc 0 0 example 명령어를 통해 정의된 가상의 원주를 따라 호가 그려진다

    위 그림에서 붉은 점은 필자가 M 명령어를 사용하여 이동한 시작점을 의미하고 노란 점은 A 명령어의 가장 마지막 인자로 할당한 (10, 50) 좌표에 있는 끝점을 의미한다.

    파란색 화살표는 SVG가 실제로 선을 렌더하는 방향을 나타낸 것인데, 실제로 저 시작점부터 끝점을 향하면서 반시계 방향으로 작은 호를 그릴 수 있는 방법은 저것밖에 없다. (잘 이해가 안 간다면 종이에 직접 그려보면 감이 온다)

    그렇다면 만약 이 호의 시작점과 끝점을 뒤바꾼다면 어떻게 될까? 이번에는 아까와 반대로 시작점을 (10, 50)으로 옮기고 끝점을 (50, 10)으로 변경하겠다.

    <svg width="500" height="500" viewBox="0 0 100 100">
  <path d="
    M 10 50
    A 40 40, 0, 0, 0, 50 10"
    stroke="green"
    fill="transparent" />
</svg>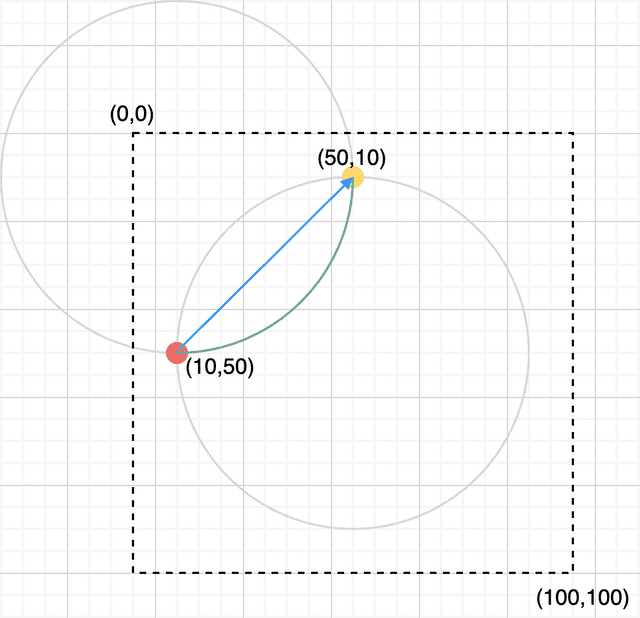
    arc 0 1 example 대척점에 있는 가상의 원을 따라 호가 그려지는 모습

    이번에도 같은 반지름을 가진 원을 따라 호가 그려졌지만, 이번에는 첫번째 예시의 원과 대척점에 있는 다른 가상의 원을 따라 호가 그려진다.

    왜냐하면 아까와 마찬가지로 저 시작점부터 끝점을 향하면서 반시계 방향으로 작은 호를 그릴 수 있는 방법이 저것밖에 없기 때문이다. 만약 이 시작점과 끝점을 이으면서 첫번째 예시의 원을 따라서 호를 그려보면 반시계 방향이 아니라 시계 방향이 된다.

    이게 바로 쓸기 플래그의 원리이다. 굳이 시작점과 끝점을 뒤바꿀 필요 없이 선을 그리는 방향만 바꿔주면 이 두 가지 호를 모두 정의할 수 있게 되기 때문이다.

    큰 호 플래그

    큰 호 플래그는 시작점과 끝점을 잇는 호 중에 작은 호를 그릴 것인지, 큰 호를 그릴 것인지를 선택한다. 위에서 보았듯이 SVG는 호를 렌더하기 위해 2개의 가상의 원을 정의하기 때문에 큰 호나 작은 호 같은 개념이 존재하게된다.

    작은 호에 대한 예시는 방금 전 그림에서 보았으니 이번에는 큰 호를 그릴 경우 SVG가 어떤 경로를 선택하여 호를 그리는 지 살펴보자.

    만약 쓸기 플래그가 0, 즉 반시계 방향이라면 각각 큰 호와 작은 호는 이 경로가 된다.

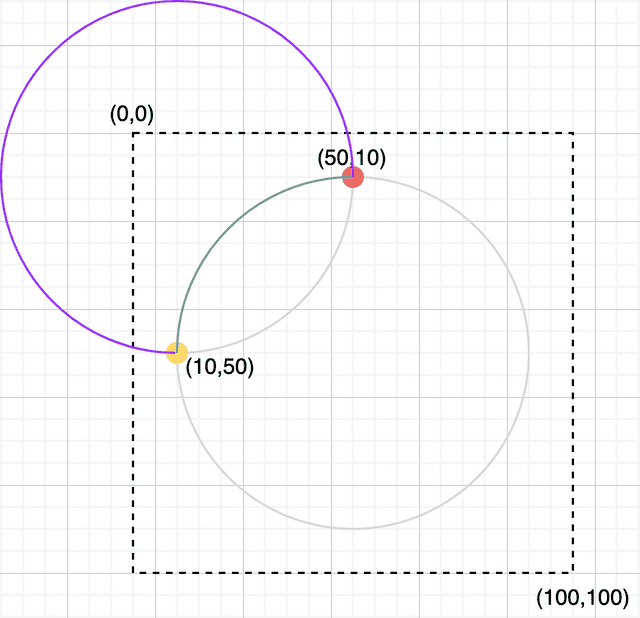    arc 1 0 example 쓸기 플래그가 0인 경우 만들 수 있는 작은 호와 큰 호

    이것도 직접 그려보면 쉽게 이해할 수 있는데, 이 두 개의 가상의 원에 놓인 시작점과 끝점을 반시계 방향으로 선을 그려 이으면서 만들 수 있는 가장 작은 호와 가장 큰 호는 실제로 저 경로들 밖에 없다.

    만약 쓸기 플래그를 1로 할당하여 호를 그리는 방향을 시계방향으로 바꾼다면 위의 쓸기 플래그의 예시에서 보았던 것과 마찬가지로 대척점에 있는 가상의 원을 따라 호가 그려지게 된다.

    삼각함수로 호의 끝점 구하기

    자, 이렇게 SVG가 호가 그리는 원리를 알았다면 이제는 애니메이션을 만들면 된다. 필자가 만들려고 했던 애니메이션은 원주를 따라 그려지는 호의 중심각이 0도에서 시작해서 360도까지 스르륵 변경되게 만들면 되는 것이니 이제 그냥 만들기만 하면 되지 않을까?

    .
    .
    .
    그렇게 쉽게 끝날리가 없다

    사실 필자가 위에서 예시로 들었던 호의 중심각은 모두 90도나 270도였다. 사실 여기에는 한 가지 이유가 숨어있는데 그게 무엇일까?

    바로 호라는 녀석이 시작점과 끝점을 정의해서 그리는 녀석이기 때문이다. 즉, 원주를 따라서 이쁘게 호를 그리고 싶다면 호의 시작점과 끝점은 반드시 원주 위에 올라가 있는 좌표를 가지고 있어야 한다. 하지만 호의 각도가 90도, 180도, 270도라면 별다른 계산 없이 X축과 Y축에 올라가 있는 점을 선택하기만 되기 때문에 필자가 예시로 들었던 모든 케이스에서 이런 각도들을 선택한 것이다.

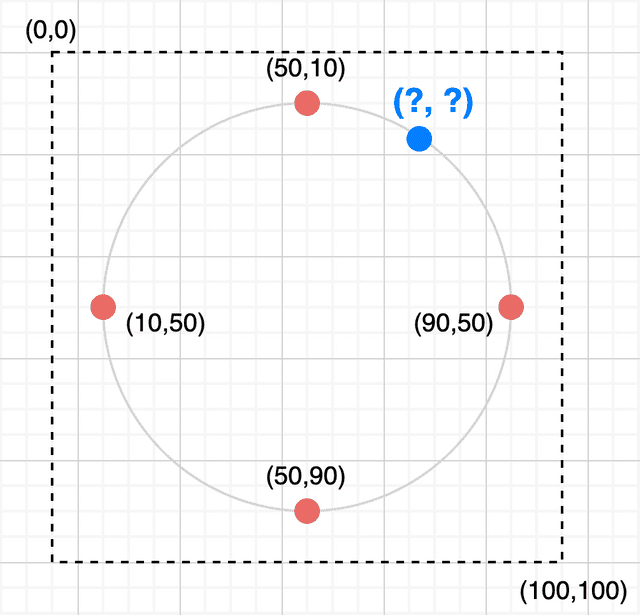    coords default 원주에 존재하는 빨간색 점의 좌표는 계산없이도 암산이 쉽지만
    파란색 점은 아니다...

    하지만 클립패스를 이루는 호의 애니메이션은 90, 180, 270, 360도로 텔레포트하면서 움직이는 것이 아니기 때문에 결국 필자는 애니메이션이 진행되는 동안 호의 끝점이 되어 줄 무수히 많은 파란점들의 좌표를 구해야한다. 이걸 어떻게 할 수 있을까?

    답은 바로 삼각함수이다.

    도와줘요 삼각함수!

    위에서도 이야기했지만 우리가 일상 속에서 호를 보았을 때 직관적으로 떠올리는 단위는 바로 각(Degree)이다. 그래서 필자는 호를 그리는 인터페이스도 이런 식으로 설계되면 편할 것이라고 생각했다.

    interface ArcData {
  x: number; // 원의 중심의 x 좌표
  y: number; // 원의 중심의 y 좌표
  radius: number; // 원의 반지름
  degree: number; // 원점에서 부터 호를 그릴 각도 
}

const drawArc = ({ x, y, radius, degree }: ArcData) => {
  return `M 어쩌고 A 어쩌고 L Z`; // 대충 호 그리는 명령어
};
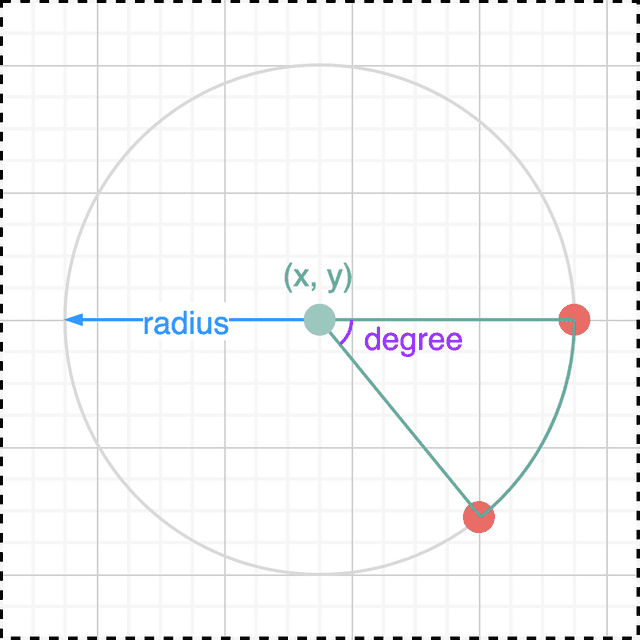    arc func 대충 행복회로의 결과물

    필자가 설계한 인터페이스처럼 임의의 각을 사용하여 호를 그리려면, 임의의 시작점을 정한 후 이 각을 이용하여 끝점의 좌표를 구해야한다.

    사실 시작점은 그냥 호를 그리기 시작할 임의의 점을 자유롭게 정하면 되기 때문에 원주 위에 있는 아무 점이나 골라잡아도 된다. 앞서 이야기했듯이 SVG는 원을 그릴 때 (cx + r, cy) 좌표를 렌더 시작점으로 정의하고 있으므로 필자도 동일하게 이 좌표를 0도의 기준으로 잡도록 하겠다.

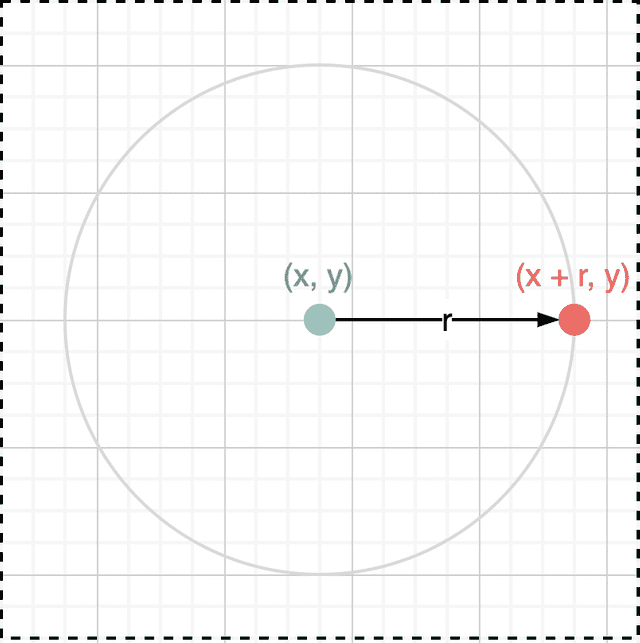    0degree 원의 중심과 저 점을 이으면 0도의 기준이 되는 시초선이 된다

    이렇게 각의 출발점이 될 시초선을 정했다면 이제 저 점으로 부터 각 θ\theta 만큼 벌렸을 때 원주 위의 어떤 점이 나오는지만 찾아내면 호를 그릴 수 있게 된다.

    이때 삼각함수를 사용하면 시초선으로부터 특정 각만큼 벌어진 선과 원주가 맞닿는 부분의 좌표를 쉽게 구할 수 있게 된다. 자 한번 어릴 때 배웠던 삼각함수를 한번 되새김질해보도록 하자.

    triangle

    이건 좌표평면 위에 정의된 반지름이 1인 원을 정의하고 xx 축을 각의 출발점인 시초선으로 정의한 후 반시계 방향으로 θ\theta 만큼 각을 진행시킨 것이다.

    이때 이 각을 타고 원주로 일직선으로 뻗어나가는 선이 만나는 지점 (x, y)가 우리가 삼각함수를 사용하여 알고 싶은 점의 좌표가 될 것이다. 그리고 이 점에서 시초선으로 수직하게 선을 내려꽂으면 위 그림과 같은 모양의 직각삼각형이 그려지게 된다.

    이때 이 삼각형의 삼각함수를 사용하여 점 (x, y)의 구성 요소인 x와 y는 이렇게 정의할 수 있다.

    sin⁡θ=ycos⁡θ=x\begin{aligned} \sin{\theta} = y \\ \cos{\theta} = x \\ \end{aligned}

    사실 이 내용은 고1 쯤에 배웠던 내용이기는 하지만, 사실 너무 오래되었던지라 필자도 오랜만에 한번 찾아봤었다. (추억의 얼싸안코가 떠오른 건 덤…)

    이게 만약 수학 문제였다면 각 θ\theta와 삼각비를 사용하여 직접 풀어내야했겠지만 다행히도 자바스크립트는 Math.sin과 Math.cos 메소드를 제공하고 있기 때문에 저걸 직접 계산하지는 않아도 된다.

    단, 여기서 한 가지 신경써줘야 할 점은 저 각 θ\theta의 단위이다. 우리가 보통 각을 생각할 때는 60분법인 90도(90°90\degree)를 떠올리지만, 사실 이렇게 “도”라는 특별한 단위가 붙은 값은 다른 일반적인 숫자와 계산이 불가능하기 때문에 이 값을 가지고는 삼각함수를 사용할 수가 없다.

    잘 이해가 되지 않는다면, 10km와 6을 더한다고 해서 16km가 되는 게 아니라는 사실을 생각해보면 조금 이해가 쉽다. 마찬가지로 10km와 6마일을 더한다고 해서 16km가 되는 것도 아니다. 단위가 붙은 어떤 물리량을 연산하려면 피연산 대상도 반드시 같은 단위가 붙어있어야 한다.

    결국 삼각함수도 일종의 함수이기 때문에 이렇게 특별한 단위가 붙은 값을 가지고는 연산을 수행할 수가 없다. 그냥 90이면 90이지, 90도라는 값으로는 삼각함수를 사용할 수가 없다는 이야기이다. 그래서 우리는 이 “도”라는 단위가 붙은 값을 단위가 없고 물리량만을 가진 호도법, 즉 라디안으로 변환해주어야한다.

    호도법, 라디안하면 어려워보일 수 있겠지만 그냥 “180도를 π\pi라디안이라고 부르자”와 같이 그냥 같은 요소를 표현하는 방법만 바뀌는 것이다. 우리가 일상생활 속에서 1근이라는 단위를 600그램으로 변환할 수 있는 것처럼 말이다.

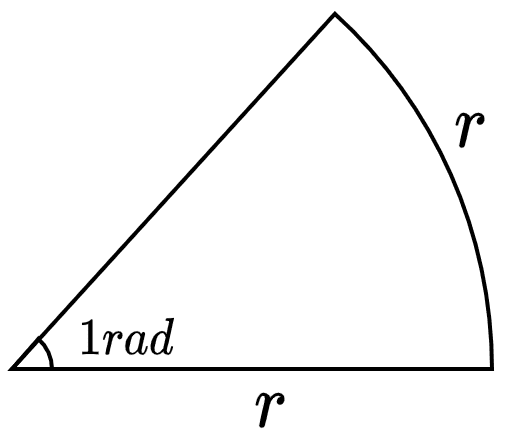
    라디안은 60분법과 마찬가지로 각을 표현하는 방법이지만, 호의 길이와 반지름의 길이를 통해 각의 크기를 정의하는 방법이기 때문에 단위가 붙지않은 순수한 숫자로만 정의된다.

    호의 길이와 반지름의 길이가 같을 때의 각도를 1라디안이라고 한다

    일단 호의 길이가 반지름의 길이와 같은 경우의 중심각을 1라디안이라고 하는 것만 알면 그 다음부터는 조금 더 쉬워진다.

    우리는 이미 원주의 전체 길이가 2πr2\pi r로 정의된다는 것을 알고 있다. 그렇다면 원을 그리려면 1라디안의 중심각을 가진 호가 몇 개나 필요할까?

    바로 2π2\pi개 이다. 즉, 원의 중심각인 360도는 1라디안에 2π2\pi를 곱한 값인 2π2\pi라디안이다.

    1라디안의 중심각을 가진 호의 길이는 무조건 원의 반지름 길이인 rr이기 때문에 전체 원주 길이를 모두 채우려면 당연히 2π2\pi개의 호가 필요하고, 이 호의 총 길이는 2πr2\pi r, 중심각은 2π2\pi라디안이라고 할 수 있는 것이다.

    여기까지 왔다면 원의 반만 채우려면 π\pi개의 호가 필요하다는 것도 쉽게 유추해볼 수 있다. 즉, 중심각이 180도인 반원의 원주 길이와 동일한 호의 개수는 π\pi개이기 때문에 180도는 π\pi라디안이 되는 것이다.

    그럼 90도는 몇 라디안일까? 90도는 다시 180도를 반으로 나눈 값이기 때문에 π2\frac{\pi}{2}라디안이 된다. 이 과정을 일반화 시켜보면 이런 모양이 된다.

    mrad=n°180°πm_{rad} = \frac{n\degree}{180\degree} \pi

    이 공식 자체는 굉장히 심플하기 때문에 코드로 작성해도 이렇게 한줄 컷이 나온다.

    const degree = 90;
const radian = (degree / 180) * Math.PI;

    라디안은 이렇게 각의 크기를 그저 호의 길이와 반지름의 길이를 사용하여 나타내는 것이라서 어떠한 단위도 붙지않기 때문에 이 값을 가지고 다른 숫자들과 자유롭게 연산을 할 수 있게 되고, 우리는 라디안으로 표현한 값과 삼각함수를 사용하여 시초선으로부터 원하는 각도에 위치한 원주 상의 좌표를 구할 수 있게 되는 것이다.

    이렇게 알아낸 모든 정보를 토대로 코드를 작성하면 이렇게 호를 그리는 path 엘리먼트의 명령어를 뱉어내는 함수를 만들 수 있다.

    // 호를 그릴 때 필요한 값들
interface ArcData {
  x: number;
  y: number;
  radius: number;
  degree: number;
}
    // 삼각함수로 시초선에서 n도 벌어진 점의 좌표를 구하는 함수
const getCoordsOnCircle = ({ x, y, radius, degree }: ArcData) => {
  const radian = (degree / 180) * Math.PI;
  return {
    x: x + radius * Math.cos(radian),
    y: y + radius * Math.sin(radian),
  };
};
    const MAX_DEGREE = 359.9;

// x, y를 중심 축으로 하여 degree(θ)만큼 +방향으로 호를 그리는 함수
export const getArc = (props: ArcData) => {
  const startCoord = getCoordsOnCircle({ ...props, degree: 0 });
  const finishCoord = getCoordsOnCircle({ ...props });

  const { x, y, radius, degree } = props;
  const isLargeArc = degree > 180 ? 1 : 0;
  const isEnd = degree === MAX_DEGREE;

  const d = `M ${startCoord.x} ${startCoord.y} A ${radius} ${radius} 0 ${isLargeArc} 1 ${finishCoord.x} ${
    finishCoord.y
  } L ${x} ${y} ${isEnd ? 'z' : ''}`;
  return d;
};

    이후 getArc 함수의 degree 값에 0 ~ 359.9을 순서대로 넘기면 애니메이션에 사용될 모든 호를 렌더할 수 있게된다. (필자는 react-spring으로 구현했다)

    이때 주의해야할 점은 호의 최대 각이 360이 아니라는 것이다. 호의 중심각이 360도가 되면 호의 시작점과 끝점의 좌표가 같아지기 때문에 SVG는 호를 렌더하지 않는다. 그래서 필자는 최대 값으로 359.9까지만 넘기고 이 값이 들어오면 Z 명령어를 사용하여 바로 시작점으로 선을 그리며 렌더를 마치도록 만들었다.

    물론 이 최대 값이 360도에 근사하면 근사할수록 더 원에 가까운 호가 그려질테지만, 어차피 사람 눈으로 보면 그 나물에 그 밥이기 때문에 그냥 이 정도만 하기로 했다.

    마치며

    사실 필자처럼 직접 도넛 차트를 구현하지 않더라도 그냥 기존에 이미 존재하는 차트 라이브러리를 사용하면 간단하게 문제를 해결할 수 있다. 하지만 필자에게 필요한 차트는 바 차트와 도넛 차트 뿐이었기 때문에 오직 이것들만을 위해 무거운 차트라이브러리를 번들에 포함시키는 것이 더 손해라고 생각했기 때문에 이렇게 직접 구현하게 되었다. (물론 예상보다 시간을 많이 쓰긴 했다)

    간혹 이렇게 2D나 3D 그래픽스를 사용한 작업을 하다보면 삼각함수나 선형대수 같은 수학 이론이 필요한 경우가 있다. 어떤 분들은 이렇게 수학적인 지식이 필요한 예제를 보면 “난 수학을 못 해서 안돼”라고 생각하고 포기하실 수도 있겠지만, 필자도 수학을 잘 하는 것이 절대 아니다.

    사실 필자는 수능 볼 때도 수학 공부를 하나도 안 했고, 그냥 OMR 카드의 답안을 일자로 쭉 그어버리고 자버려서 8등급이 나온 사람이다. 아마 필자 밑에 있던 녀석들도 전부 필자처럼 아예 수학을 포기하고 찍고 자버린 녀석들일 것이다. 이렇게 아예 공부를 안 했던 필자도 이해할 수 있을 정도면 아마 대부분의 사람들도 조금만 고민하고 생각해보면 충분히 이해할 수 있는 것들이라고 생각한다.

    물론 이론이나 공식들을 깊게 파고들려고 하면 끝이 없기도 하고 어렵기도 하다. 아니, 어차피 봐도 이해를 못 할 가능성이 더 높다. 하지만 실제로 우리가 어플리케이션을 만들 때 만나는 문제를 해결할 정도의 수학 이론이나 공식은 이해하기가 그리 어렵지도 않은 편이라고 생각한다.

    어린 시절 학교에서는 삼각함수를 알려줄 때 이 이론이나 함수가 어떤 문제를 해결할 수 있는지에 대해서는 알려주지 않고, 그저 시험을 위해 공식과 이론들을 외우게만 시켰었다. (수업시간에 그렇게 잤는데도 얼싸안코는 기억이 난다…)

    하지만 지금은 그 때와 다르다. 이 공식이나 이론들이 어떤 문제를 해결할 수 있는지도 명확히 알고 있을 뿐더러 그 문제를 겪고 있는 당사자가 바로 나이기 때문에, 수능만을 위해 공부하던 그때보다 동기 부여도 더 확실하게 될 수 있다고 생각한다.

    이상으로 SVG와 삼각 함수로 도넛 차트 만들어보기 포스팅을 마친다.

    Evan Moon

    🐢 거북이처럼 살자

    개발을 잘하기 위해서가 아닌 개발을 즐기기 위해 노력하는 개발자입니다. 사소한 생각 정리부터 튜토리얼, 삽질기 정도를 주로 끄적이고 있습니다.